Определение центров тяжести плоских сечений, составленных из стандартных профилей проката и из простейших геометрических фигур

Тема:Центр тяжести.

Цель работы: научить определять центр тяжести сложных сечений.

1. Разбивают сечение на простые фигуры. В задачах такими фигурами являются стандартные профили проката. Обычно профили прокатной стали, образующие сечение, обозначают цифрами 1,2,3… .

2. Указывают центры тяжести каждого профиля (фигуры) и обозначают их С¹, С₂…, С_n, используя таблицы ГОСТОв (см. прилож.1.)

3. Выбирают систему координатных осей. Рекомендуется одну из координатных осей совмещать с осью симметрии. Вторую ось координат направляют перпендикулярно первой так, чтобы она пересекла центры тяжести одной или нескольких фигур. При этом начало координат может совпадать (или не совпадать) с центром тяжести из фигур. Вторую ось можно направить так, чтобы она прошла через нижнюю (крайнюю) точку сечения. В первом случае вычисления будут более простыми.

4. Составляют формулы для определения координат центра тяжести сечения:

1) х_с = ;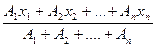

2) у_с = .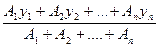

Пользуясь таблицами ГОСТов (см. прилож. 1), определяют площади профилей проката А₁, А₂…, А_n, координаты их центров тяжести х₁, х_2,…х_n и у₁, у_2,…у_n относительно выбранных осей координат. Число слагаемых в числите и знаменателе формул зависит от числа профилей, из которых состоит сечение. Полученные величины подставляют в формулу и находят х_с и у_с.

Следует помнить, что если ось х совмещена с осью симметрии, то координата у_с = 0, а если ось у совмещена с осью симметрии, то х_с =0.

5. Указывают положение центра тяжести на рисунке, придерживаясь определенного масштаба, и показывают расстояние от центра тяжести до координат осей.

6. Выполняют проверку правильности решения, для чего можно изменить положение координатных осей (или одной оси) и найти координаты центра тяжести относительно новых осей. Положение центра тяжести не зависит от того, как выбрана система координатных осей.

Пример 3.1. Определить координаты центра тяжести сечения, составленного из профилей проката, как показано на рис.3. Сечение состоит из двутавровой балки № 33, швеллера № 27, двух уголков 90х56х6 мм и листа сечением 12х180 мм.

Решение 1.Разобьем сечение в соответствии с профилями проката и обозначим их 1,2,3,4,5.

2. Пользуясь таблицей укажем центры тяжести каждого профиля и обозначим их С₁, С₂, С₃, С₄, и С₅.

3. Выберем систему осей координат. Ось у совместим с осью симметрии, а ось х направим перпендикулярно оси у и проведем через центр тяжести двутавровой балки.

4. Выпишем формулы для определения координат центра тяжести сечения:

х_с = 0, так как ось у совпадает с осью симметрии;

у_с = .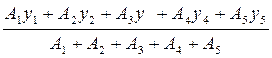

Учитывая, что А₂ = А₃, а также, что у₂ = у_3, получим:

у_с = .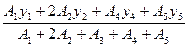

Определим площади и координаты центров тяжести отдельных профилей проката, используя сечение и таблицы 2,3,4 прилож. 1

А₁ = 35,2 см²; А₂ = А₃= 8,54 см²; А₄ = 53,8 см²;

А₅ = 1,2 ·18 = 21,6 см²;

у₁ = h_дв/2 + d_шв –z_0(шв) =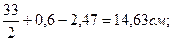

у₂ = у₃ = h_дв/2 + d_шв – b_шв + х_0(уг) =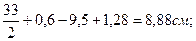

у₄ = 0, так как ось х проходит через центр тяжести двутавра;

у₅ = - (h_дв/2 + δ_листа/2) = -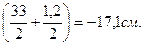

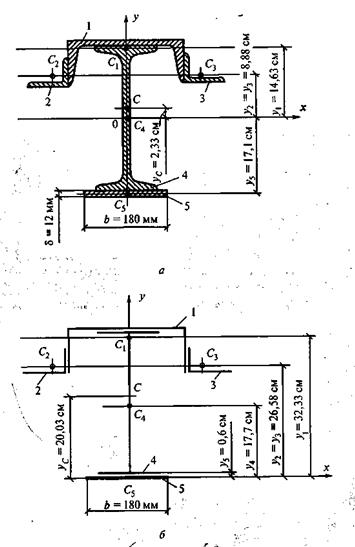
Рис. 3

Поставим полученные значения в формулу для определения у_с:

у_с =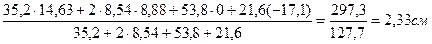

Укажем положение центра тяжести сечения С (см рис. 3 а).

5. Проверка решения. Проведем ось х по нижней грани листа (рис. 3 б.). Площади профилей останутся теми же, а координаты центров тяжести изменятся:

у₁ = δ_листа + h_дв + d_шв – z_0(шв) = 1,2 + 33 + 0,6 – 2,47 = 32,33 см;

у₂ = δ_листа + h_дв + d_шв – b_шв – х_0(уг) = 1,2 + 33 + 0,6 – 9,5 - 1,28 = 26,58 см;

у₂ = у₃ = 26,58 см;

у₄ = δ_листа + h_дв/2 = 1,2 +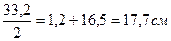

у₅ = δ_листа /2 = .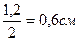

Определим положение центра тяжести в новой системе координат

у_с =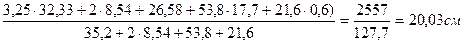

Разность между координатами центра тяжести должна быть равна расстоянию между осями х в первом и во втором решении:

20,3 – 2,33 = 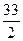+ 1,2,

откуда 17,7 см = 17,7 см.

Ответ: у_с = 2,33 см, если ось х проходит через С₄ , и у_с = 20,03 см, если ось х проходит по нижней грани.

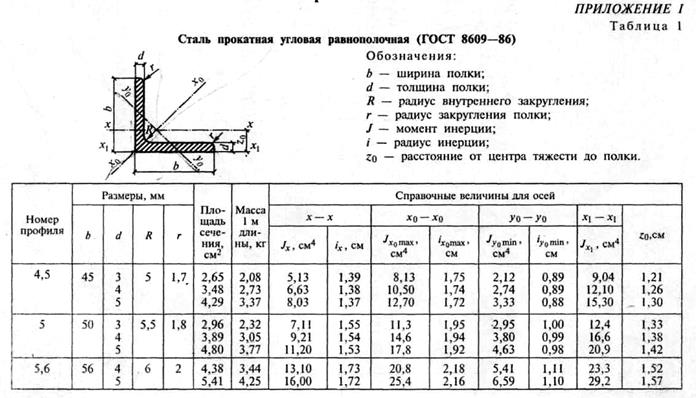
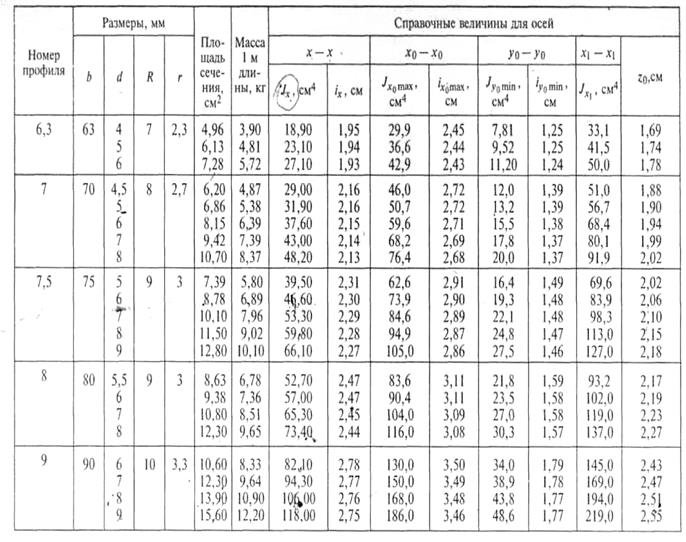
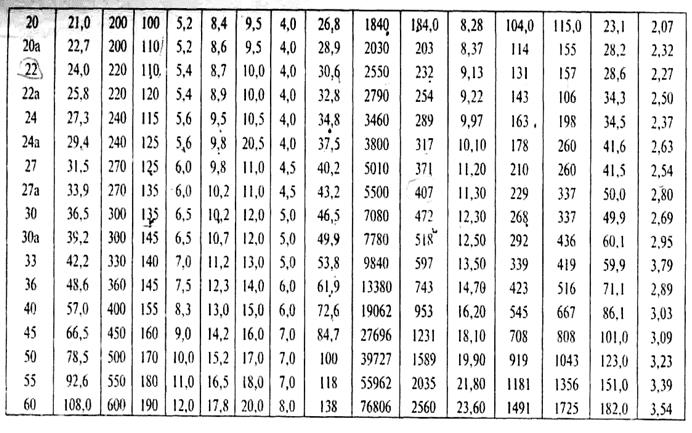
Продолжение таблицы № 1

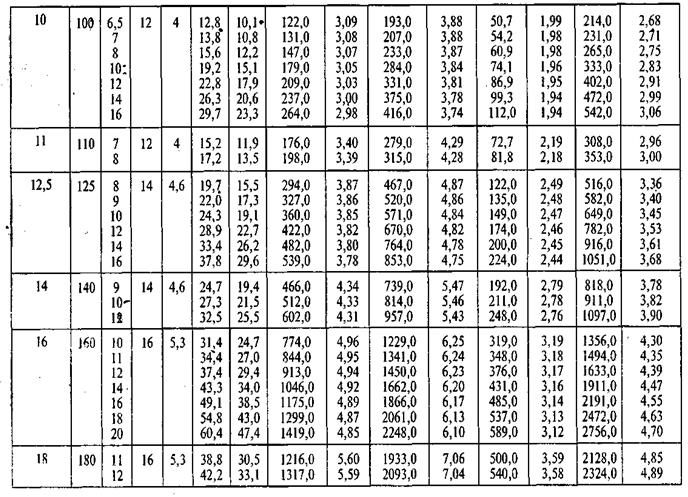
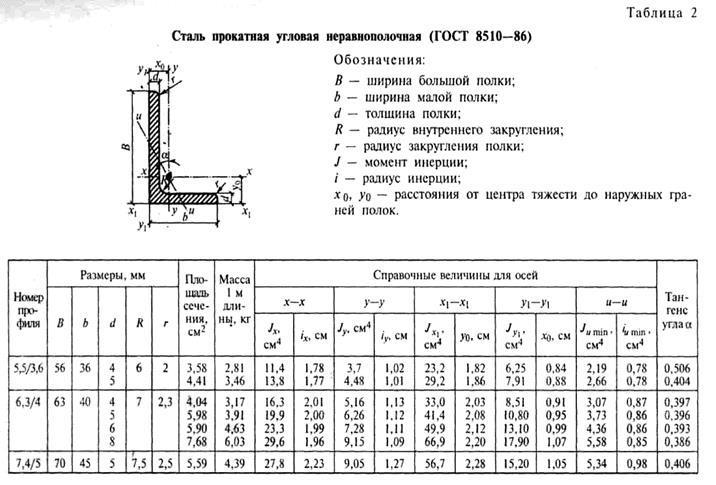
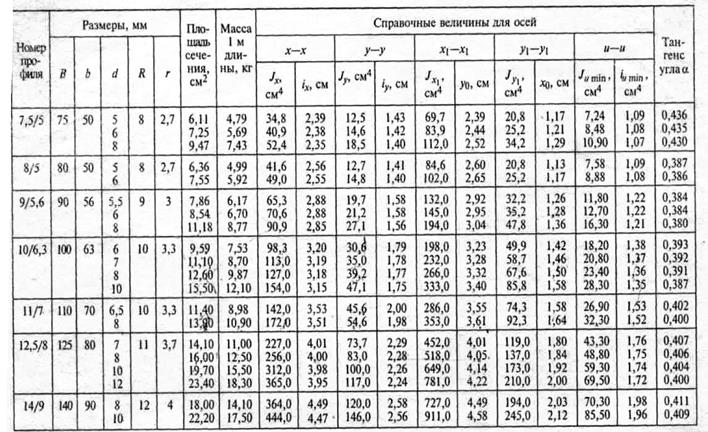
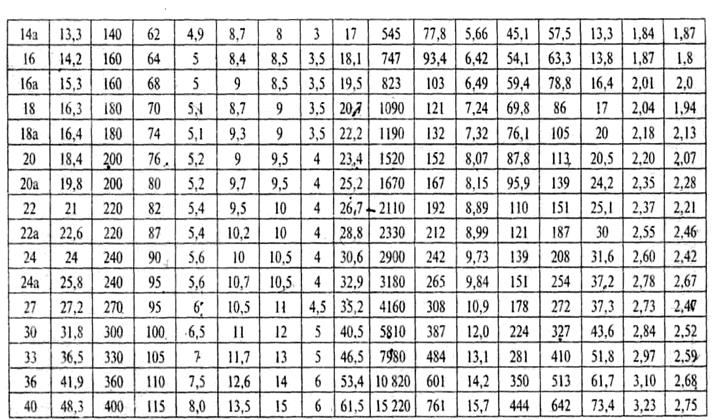
Продолжение таблицы № 2

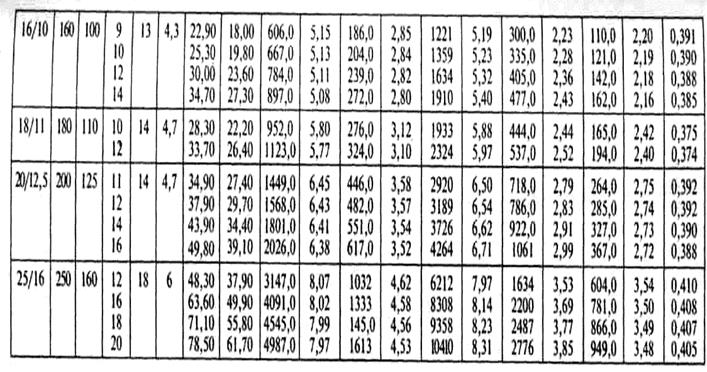
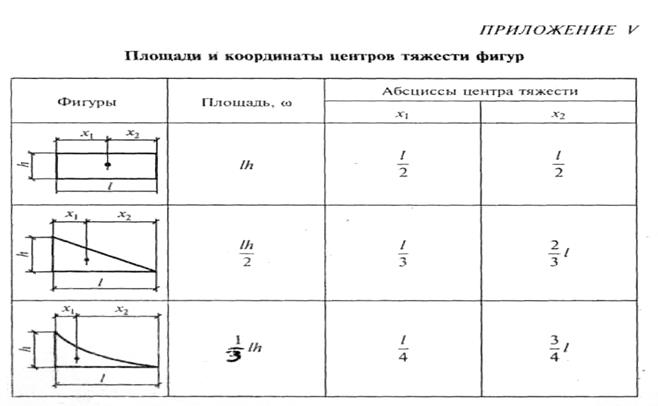
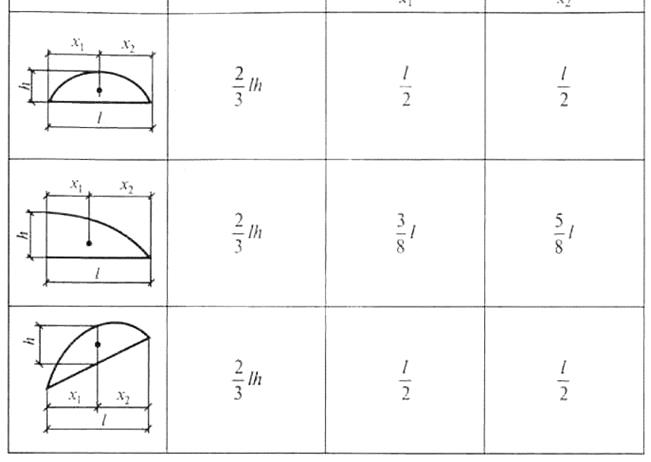
Таблица 3

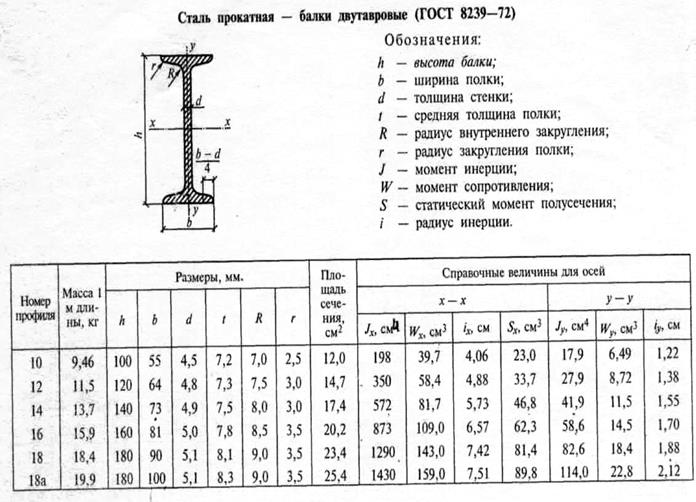
Список литературы

1. А.И. Аркуша «Техническая механика». Высшая школа 2003.

2. В.Э. Зависновский, Н.М. Захаров. «Техническая механика» ООО «Амалфея» 2000 г.

3. В.И. Сетков. Сборник задач по технической механике». М.: 2003.