Комбинация многоугольников и окружностей
Задание 26 № 52
1.Основание 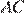 равнобедренного треугольника
равнобедренного треугольника  равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания
равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания 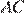 в его середине . Найдите радиус окружности, вписанной в треугольник
в его середине . Найдите радиус окружности, вписанной в треугольник  .
.
Решение.
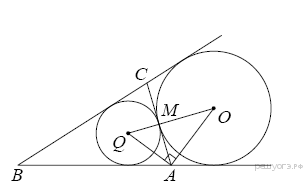
Пусть 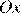 — центр данной окружности, а
— центр данной окружности, а 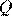 — центр окружности, вписанной в треугольник
— центр окружности, вписанной в треугольник  . Точка касания
. Точка касания 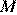 окружностей делит
окружностей делит 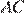 пополам.
пополам. 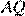 и
и 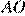 — биссектрисы смежных углов, значит, угол
— биссектрисы смежных углов, значит, угол 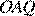 прямой. Из прямоугольного треугольника
прямой. Из прямоугольного треугольника 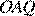 получаем:
получаем: 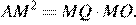
Следовательно,
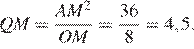
Ответ: 4,5.
----------
Дублирует задание 314827.
Критерии проверки:
Источник: Демонстрационная версия ГИА—2013 по математике.
Задание 26 № 339825
2.В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
Решение.
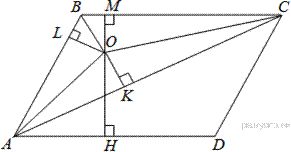 Проведём построения и введём обозначения как показано на рисунке. Пусть
Проведём построения и введём обозначения как показано на рисунке. Пусть 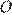 — центр окружности, вписанной в треугольник
— центр окружности, вписанной в треугольник 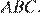 Центр вписанной окружности — это точка пересечения биссектрис, поэтому
Центр вписанной окружности — это точка пересечения биссектрис, поэтому 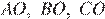 — биссектрисы. Из прямоугольного треугольника
— биссектрисы. Из прямоугольного треугольника 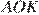 по теореме Пифагора найдём
по теореме Пифагора найдём 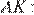
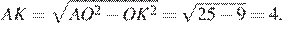
Отрезки 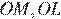 и
и 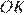 равны как радиусы вписанной в треугольник
равны как радиусы вписанной в треугольник  окружности, то есть
окружности, то есть 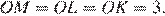 Рассмотрим треугольники ALO и AOK, они прямоугольные, углы
Рассмотрим треугольники ALO и AOK, они прямоугольные, углы 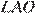 и
и 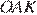 равны,
равны, 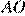 — общая, следовательно, треугольники равны, откуда
— общая, следовательно, треугольники равны, откуда 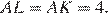 Аналогично из равенства треугольников
Аналогично из равенства треугольников 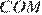 и
и 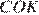 получаем
получаем 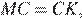 а из равенства треугольников
а из равенства треугольников 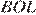 и
и 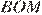 —
— 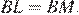 Площадь треугольника
Площадь треугольника  можно найти как произведение радиуса вписанной окружности на полупериметр:
можно найти как произведение радиуса вписанной окружности на полупериметр:
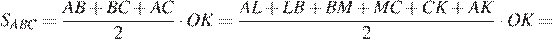
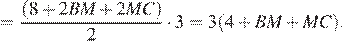
Площадь параллелограмма равна произведению высоты на основание:
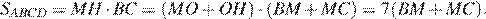
Рассмотрим треугольники  и
и 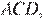
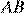 равно
равно 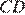 ,
, 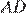 равно
равно 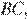 углы
углы  и
и 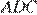 равны, следовательно, треугольники
равны, следовательно, треугольники  и
и 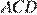 равны. Поэтому площадь треугольника
равны. Поэтому площадь треугольника  равна половине площади параллелограмма:
равна половине площади параллелограмма:
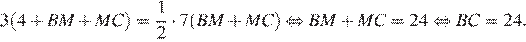
Площадь параллелограмма равна: 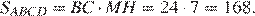
Ответ: 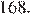
Критерии проверки:
Задание 26 № 339886
3.Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Решение.
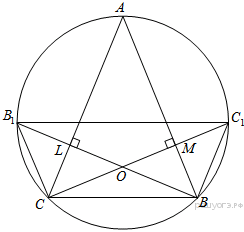 ВВедём обозначения как показано на рисунке. Отрезок
ВВедём обозначения как показано на рисунке. Отрезок 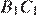 проходит через центр описанной окружности, следовательно,
проходит через центр описанной окружности, следовательно, 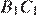 — диаметр. Углы
— диаметр. Углы 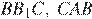 и
и 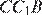 — вписанные и опираются на одну и ту же дугу, значит, они равны. Из прямоугольного треугольника
— вписанные и опираются на одну и ту же дугу, значит, они равны. Из прямоугольного треугольника 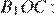
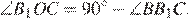 Из прямоугольного треугольника
Из прямоугольного треугольника 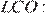
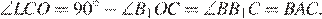 Рассмотрим прямоугольный треугольник
Рассмотрим прямоугольный треугольник 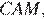 углы
углы 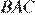 и
и 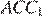 равны, значит
равны, значит 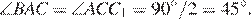
Ответ: 45°.
Критерии проверки:
Задание 26 № 340855
4.В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 14, BC = 12.
Решение.
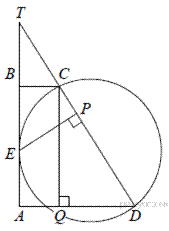 Пусть T — точка пересечения прямых AB и CD, P — проекция точки E на прямую CD, Q — проекция точки C на прямую AD (см. рис.). Обозначим ∠CDA = a, CD = x.
Пусть T — точка пересечения прямых AB и CD, P — проекция точки E на прямую CD, Q — проекция точки C на прямую AD (см. рис.). Обозначим ∠CDA = a, CD = x.
Поскольку QD = AD − AQ = AD − BC = 2, получаем, что 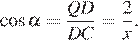
Из подобия треугольников TBC и TAD находим, что TC = 6x.
Поэтому
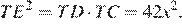
Следовательно,
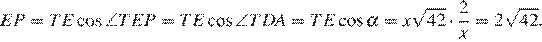
Ответ: 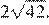
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 26.11.2014 вариант МА90201.
Задание 26 № 340907
5.В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 15 , BC = 14.
Решение.
 Пусть T — точка пересечения прямых AB и CD, P — проекция точки E на прямую CD, Q — проекция точки C на прямую AD (см. рис.). Обозначим ∠CDA = α, CD = x.
Пусть T — точка пересечения прямых AB и CD, P — проекция точки E на прямую CD, Q — проекция точки C на прямую AD (см. рис.). Обозначим ∠CDA = α, CD = x.
Поскольку QD = AD − AQ = AD − BC = 1, получаем, что 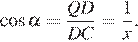
Из подобия треугольников TBC и TAD находим, что TC = 14x.
Поэтому
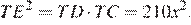
Следовательно,
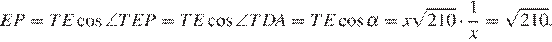
Ответ: 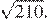
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 26.11.2014 вариант МА90203.
Задание 26 № 340936
6.В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 16 , BC = 8.
Решение.
 Пусть T — точка пересечения прямых AB и CD, P — проекция точки E на прямую CD, Q — проекция точки C на прямую AD (см. рис.). Обозначим ∠CDA = α, CD = x.
Пусть T — точка пересечения прямых AB и CD, P — проекция точки E на прямую CD, Q — проекция точки C на прямую AD (см. рис.). Обозначим ∠CDA = α, CD = x.
Поскольку QD = AD − AQ = AD − BC = 8, получаем, что 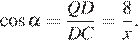
Из подобия треугольников TBC и TAD находим, что TC = x.
Поэтому
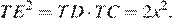
Следовательно,
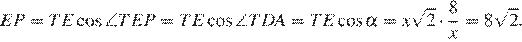
Ответ: 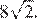
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 26.11.2014 вариант МА90204.
Задание 26 № 341345
7.В треугольнике ABC на его медиане BM отмечена точка K так, что BK : KM = 7 :3 . Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника BKP к площади четырёхугольника KPCM.
Решение.
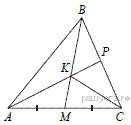 Медиана KM разбивает треугольник AKC на два равновеликих треугольника — пусть их площади равны по 3S. Поскольку
Медиана KM разбивает треугольник AKC на два равновеликих треугольника — пусть их площади равны по 3S. Поскольку 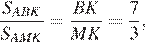 получаем, что
получаем, что 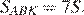
Пусть 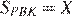 и
и 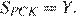 Тогда
Тогда 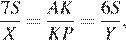 отсюда
отсюда 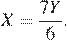 Далее,
Далее, 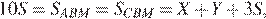 а тогда
а тогда 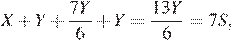 то есть
то есть 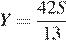 и
и 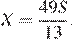
Получаем, что 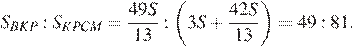
Ответ: 49 : 81.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.04.2015 вариант МА90701.
Задание 26 № 341371
8.В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ = 14, SQ = 4 .
Решение.
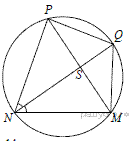 Поскольку ∠QPS = ∠QPM = ∠MNQ = ∠QNP (см. рис.), треугольник PQS подобен треугольнику NQP по двум углам (угол при вершине Q общий). Поэтому
Поскольку ∠QPS = ∠QPM = ∠MNQ = ∠QNP (см. рис.), треугольник PQS подобен треугольнику NQP по двум углам (угол при вершине Q общий). Поэтому 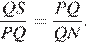
Пусть NS = x. Тогда 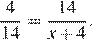
Из этого уравнения находим, что x = 45.
Ответ: 45.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.04.2015 вариант МА90702.
Задание 26 № 341397
9.Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 96, тангенс угла BAC равен 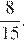 Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
Решение.
Заметим, что ∠CAB = 90° − ∠CBA = ∠PCB, так что треугольник ABC подобен треугольнику CBP.
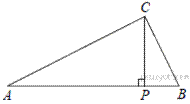
Пусть радиус окружности, вписанной в треугольник ABC, равен r, тогда 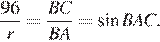 Поскольку тангенс угла BAC равен
Поскольку тангенс угла BAC равен 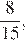 получаем, что,
получаем, что, 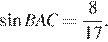 Значит,
Значит, 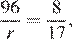 откуда r = 204.
откуда r = 204.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.04.2015 вариант МА90703.
Задание 26 № 341512
10.На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC = 40, BC = 34 и CD = 20.
Решение.
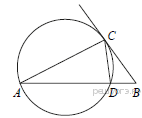 Из теоремы об угле между касательной и хордой следует, что ∠BCD = ∠CAD = ∠CAB, значит, треугольник ABC подобен треугольнику CBD по двум углам, причём коэффициент подобия равен
Из теоремы об угле между касательной и хордой следует, что ∠BCD = ∠CAD = ∠CAB, значит, треугольник ABC подобен треугольнику CBD по двум углам, причём коэффициент подобия равен 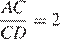 (см. рисунок). Тогда
(см. рисунок). Тогда
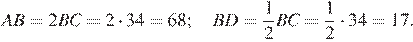
Следовательно,
Ответ: 51.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.05.2015 вариант МА90901.
Задание 26 № 311574
11.Диагонали четырёхугольника 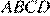 , вершины которого расположены на окружности, пересекаются в точке
, вершины которого расположены на окружности, пересекаются в точке 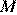 . Известно, что
. Известно, что 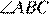 = 72°,
= 72°, 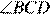 = 102°,
= 102°, 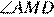 = 110°. Найдите
= 110°. Найдите 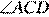 .
.
Решение.
Пусть 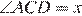 .
.
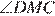 = 180° − 110° = 70°;
= 180° − 110° = 70°;
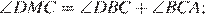
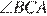 = 102° − x;
= 102° − x; 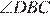 + 102° − x = 70°; x =
+ 102° − x = 70°; x = 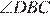 + 32°.
+ 32°.
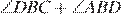 = 72°;
= 72°; 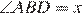 ;
; 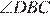 = 72° − x; 2x = 104°, x=52°.
= 72° − x; 2x = 104°, x=52°.
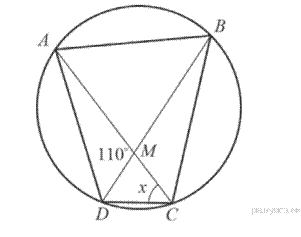
Ответ: 52°.
Критерии проверки:
Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар)
Задание 26 № 311703
12.Длина катета 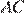 прямоугольного треугольника
прямоугольного треугольника  равна 8 см. Окружность с диаметром
равна 8 см. Окружность с диаметром 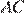 пересекает гипотенузу
пересекает гипотенузу 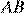 в точке
в точке 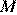 . Найдите площадь треугольника
. Найдите площадь треугольника  , если известно, что
, если известно, что 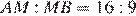 .
.
Решение.
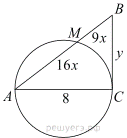
Пусть 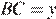 см,
см, 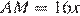 см и
см и 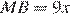 см. Поэтому гипотенуза
см. Поэтому гипотенуза 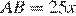 см. По теореме Пифагора:
см. По теореме Пифагора:
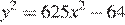 .
.
По теореме о секущей и касательной
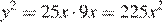 .
.
Следовательно, 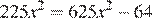 , откуда
, откуда 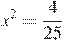 .
.
Тогда 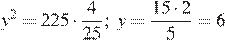 .
.
Следовательно, площадь треугольника равна
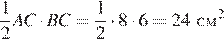 .
.
Ответ: 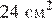 .
.
Критерии проверки:
Источник: ГИА-2012. Математика. Тренировочная работа №1 (1 вар.)
Задание 26 № 341423
13.Углы при одном из оснований трапеции равны 85° и 5°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 1. Найдите основания трапеции.
Решение.
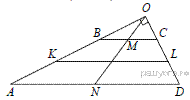 Пусть ABCD — данная трапеция, AD — большее основания, K и L — середины сторон AB и CD соответственно. Сумма углов при одном из оснований равна 85° + 5° = 90°, так что это большее основание AD.
Пусть ABCD — данная трапеция, AD — большее основания, K и L — середины сторон AB и CD соответственно. Сумма углов при одном из оснований равна 85° + 5° = 90°, так что это большее основание AD.
Продолжим боковые стороны трапеции до пересечения в точке O (см. рис.).
Легко видеть, что ∠AOD = 180° − (85° + 5°) = 90°.
Пусть N — середина отрезка AD. Тогда 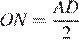 — медиана прямоугольного треугольника AOD. Поскольку медиана ON делит пополам любой отрезок с концами на сторонах AO и DO треугольника AOD, параллельный стороне AD, она пересекает основание BC также в его середине M.
— медиана прямоугольного треугольника AOD. Поскольку медиана ON делит пополам любой отрезок с концами на сторонах AO и DO треугольника AOD, параллельный стороне AD, она пересекает основание BC также в его середине M.
Значит, 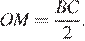 Таким образом,
Таким образом, 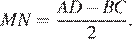 Средняя линия KL трапеции при этом равна
Средняя линия KL трапеции при этом равна 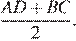
Получаем, что AD = MN + KL = 11 + 1 = 12; BC = KL − MN = 11 −1 = 10.
Ответ: 12; 10.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.04.2015 вариант МА90704.
Задание 26 № 341538
14.Боковые стороны AB и CD трапеции ABCD равны соответственно 28 и 35, а основание BC равно 7. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение.
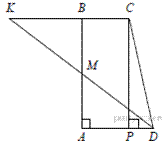 Пусть M — середина AB (см. рис.). Продолжим биссектрису DM угла ADC до пересечения с продолжением основания BC в точке K. Поскольку ∠CKD = ∠ADK = ∠CDK, треугольник KCD равнобедренный, KC = CD = 35. Тогда KB = KC − BC = 35 − 7 = 28.
Пусть M — середина AB (см. рис.). Продолжим биссектрису DM угла ADC до пересечения с продолжением основания BC в точке K. Поскольку ∠CKD = ∠ADK = ∠CDK, треугольник KCD равнобедренный, KC = CD = 35. Тогда KB = KC − BC = 35 − 7 = 28.
Из равенства треугольников AMD и BMK следует, что AD = BK = 28. Проведём через вершину C прямую, параллельную стороне AB, до пересечения с основанием AD в точке P. Треугольник CPD прямоугольный, так как CD2 = 352 = 282+ + 212 = PC2+ + PD2.
Поэтому CP — высота трапеции. Следовательно,
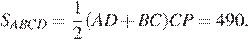
Ответ: 490.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.05.2015 вариант МА90902.
Задание 26 № 130
15.Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен  . Найдите радиус вписанной окружности треугольника ABC.
. Найдите радиус вписанной окружности треугольника ABC.
Решение.
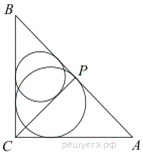
Угол BAC равен углу BCP так как 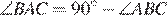 и
и 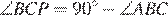 . Так как тангенс это отношение противолежащего катета к прилежащему, имеем:
. Так как тангенс это отношение противолежащего катета к прилежащему, имеем: 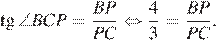 Тогда
Тогда 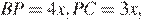 а гипотенуза
а гипотенуза  по теореме Пифагора. Площадь треугольника равна произведению половины его периметра на радиус вписанной окружности, но площадь прямоугольного треугольника равна половине произведения катетов, имеем:
по теореме Пифагора. Площадь треугольника равна произведению половины его периметра на радиус вписанной окружности, но площадь прямоугольного треугольника равна половине произведения катетов, имеем:
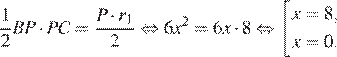
Таким образом, 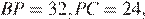 а
а 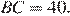 Так как
Так как 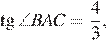 то
то 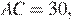 а
а  по теореме Пифагора.
по теореме Пифагора.
В треугольнике  площадь равна произведению половины его периметра на радиус вписанной в него окружности, но площадь прямоугольного треугольника равна половине произведения катетов, имеем:
площадь равна произведению половины его периметра на радиус вписанной в него окружности, но площадь прямоугольного треугольника равна половине произведения катетов, имеем:
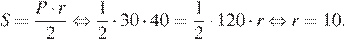
Ответ: 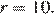
Критерии проверки:
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1309.
Задание 26 № 311705
16.На каждой из двух окружностей с радиусами 3 и 4 лежат по три вершины ромба. Найдите его сторону.
Решение.
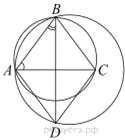
Пусть вершины 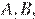 и
и  ромба
ромба 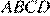 лежат на окружности радиуса 3, а вершины
лежат на окружности радиуса 3, а вершины 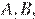 и
и 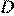 лежат на окружности радиуса 4. Примем сторону ромба за
лежат на окружности радиуса 4. Примем сторону ромба за 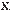 , а величину угла
, а величину угла 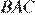 за
за 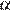 .
.
Тогда по теореме синусов для треугольника 
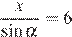 .
.
Аналогично по теореме синусов для треугольника 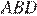 :
:
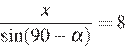 .
.
Значит, 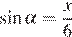 и
и 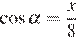 . Получаем уравнение
. Получаем уравнение
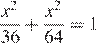 .
.
Откуда 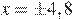 . Следовательно, сторона ромба равна 4,8.
. Следовательно, сторона ромба равна 4,8.
Ответ: 4,8.
Критерии проверки:
Источник: ГИА-2012. Математика. Тренировочная работа № 2(1 вар)
Задание 26 № 156
17.Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Решение.
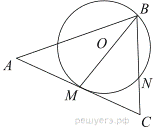
Медиана BM делит AC пополам. Центр окружности лежит на середине медианы BM, тогда ON — средняя линия в треугольнике BMC, где O — центр окружности, а N — точка пересечения этой окружности стороны BC. Средняя линия в треугольнике равна половине основания, поэтому ON = 1. Средняя линия ON является радиусом окружности. Так как медиана BM является диаметром, то BM = 2ON = 2. Проведем MN в треугольнике BMC. Так как угол BNM опирается на диаметр BM, то 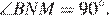 таким образом, треугольник BNM — прямоугольный. Так как MN — средняя линия, то она параллельна AB, тогда треугольник ABC — прямоугольный. Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы, таким образом, радиус описанной вокруг треугольника ABC окружности равен 2.
таким образом, треугольник BNM — прямоугольный. Так как MN — средняя линия, то она параллельна AB, тогда треугольник ABC — прямоугольный. Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы, таким образом, радиус описанной вокруг треугольника ABC окружности равен 2.
Критерии проверки:
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1313.
Задание 26 № 315126
18.Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Решение.
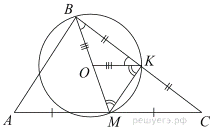
Введём обозначения как показано на рисунке. Рассмотрим треугольник 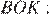 — он равнобедренный, следовательно,
— он равнобедренный, следовательно, 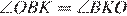 . Аналогично в треугольнике
. Аналогично в треугольнике 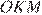 имеем:
имеем: 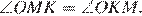 Теперь рассмотрим треугольник
Теперь рассмотрим треугольник 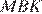 : сумма его углов равна 180°, поэтому
: сумма его углов равна 180°, поэтому
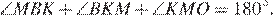
Поскольку кроме этого 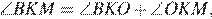 имеем:
имеем:
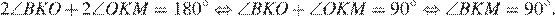
Рассмотрим треугольники 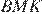 и
и 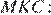 они прямоугольные, имеют общий катет и
они прямоугольные, имеют общий катет и 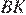 равно
равно 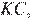 следовательно, эти треугольники равны, а значит,
следовательно, эти треугольники равны, а значит, 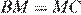 .
.
Точка 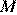 отстоит на равное расстояние от всех трёх вершин треугольника,
отстоит на равное расстояние от всех трёх вершин треугольника, 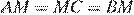 , следовательно, точка
, следовательно, точка 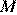 — центр окружности, описанной около треугольника
— центр окружности, описанной около треугольника  . Найдём сторону
. Найдём сторону 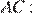
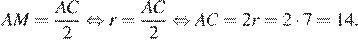
Ответ: 14.
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 26 № 314944
19.Основание AC равнобедренного треугольника ABC равно 16. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Решение.
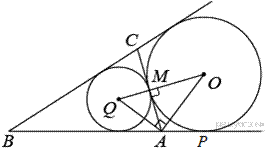 Введём обозначения, приведённые на рисунке. Лучи
Введём обозначения, приведённые на рисунке. Лучи 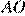 и
и 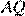 — соответственно биссектрисы углов
— соответственно биссектрисы углов 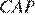 и
и 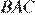 , поскольку эти лучи проходят через центры вписанных окружностей.
, поскольку эти лучи проходят через центры вписанных окружностей. 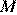 — середина основания
— середина основания 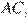 следовательно
следовательно 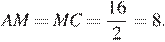 Углы
Углы 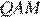 и
и 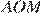 равны друг другу, как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники
равны друг другу, как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники 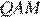 и
и 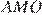 — они прямоугольные и имеют равные углы
— они прямоугольные и имеют равные углы 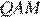 и
и 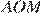 , следовательно эти треугольники подобны:
, следовательно эти треугольники подобны:
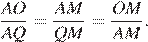
Отсюда следует, что радиус вписаной окружности:
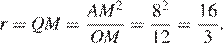
Ответ: 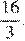
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 26 № 339675
20.Четырёхугольник ABCD со сторонами AB = 25 и CD = 16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Для решения этой задачи необходимо знание формул тригонометрии.
Решение.
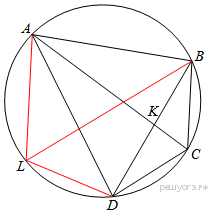 Проведём через точку
Проведём через точку 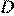 прямую, параллельную диагонали
прямую, параллельную диагонали 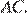 Дуги
Дуги 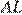 и
и 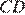 равны, следовательно, равны и стягивающие их хорды:
равны, следовательно, равны и стягивающие их хорды: 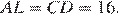
Вертикальные углы 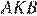 и
и 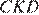 равны. Углы
равны. Углы 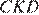 и
и 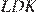 равны как накрест лежащие:
равны как накрест лежащие: 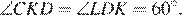
Четырёхугольник 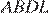 вписан в окружность, следовательно, суммы противолежащих углов равны 180°, откуда
вписан в окружность, следовательно, суммы противолежащих углов равны 180°, откуда 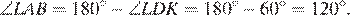
Рассмотрим треугольник 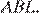 По теореме косинусов:
По теореме косинусов:
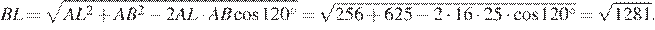
Найдём радиус описанной вокруг треугольника 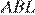 окружности по теореме синусов:
окружности по теореме синусов: 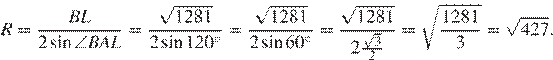
Ответ: 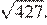
Приведём другое решение.
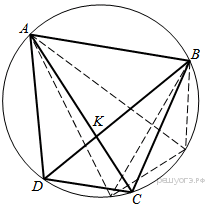
Передвинем хорду 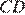 так, чтобы она стала параллельна стороне
так, чтобы она стала параллельна стороне 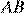 (см. рисунок). Заметим, что при таком движении угол
(см. рисунок). Заметим, что при таком движении угол 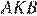 остаётся равен 60°, поскольку он равен полусумме дуг
остаётся равен 60°, поскольку он равен полусумме дуг 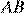 и
и 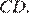 Параллельные прямые отсекают равные дуги, поэтому дуги
Параллельные прямые отсекают равные дуги, поэтому дуги 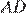 и
и 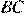 равны. Углы
равны. Углы 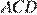 и
и 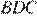 равны, как вписанные углы, опирающиеся на равные дуги. Таким образом, треугольник
равны, как вписанные углы, опирающиеся на равные дуги. Таким образом, треугольник 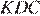 — равнобедренный:
— равнобедренный:
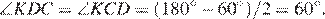
Все углы треугольника 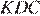 равны 60°, следовательно, треугольник
равны 60°, следовательно, треугольник 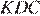 — равносторонний, значит
— равносторонний, значит 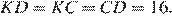 Аналогично можно показать, что треугольник
Аналогично можно показать, что треугольник 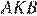 — равносторонний, откуда
— равносторонний, откуда 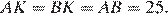
Рассмотрим треугольник 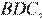
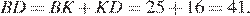 По теореме косинусов:
По теореме косинусов:
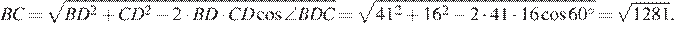
По теореме синусов: 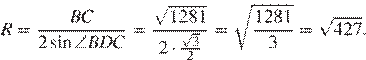
Приведём другое решение.
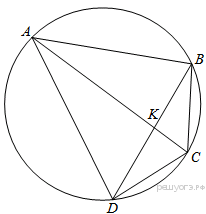
Рассмотрим треугольник 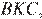 сумма углов треугольника равна 180°:
сумма углов треугольника равна 180°: 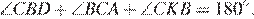 Углы
Углы 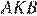 и
и 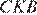 являются смежными, следовательно,
являются смежными, следовательно, 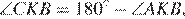 откуда:
откуда:
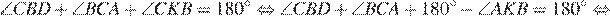
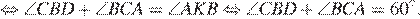
Пусть 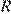 — радиус описанной окружности, угол
— радиус описанной окружности, угол 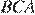 обозначим как
обозначим как 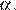 Рассмотрим треугольник
Рассмотрим треугольник 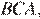 он вписан в окружность, следовательно, по теореме синусов:
он вписан в окружность, следовательно, по теореме синусов:
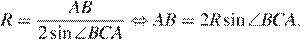
Аналогично, из треугольника 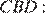
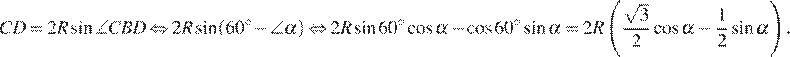
Разделим 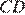 на
на 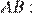
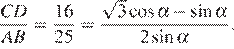
Откуда:

Найдём 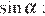
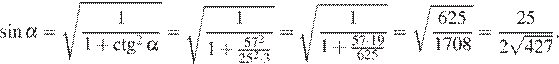
Таким образом, радиус описанной окружности равен:
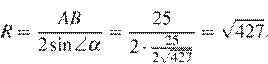
Критерии проверки:
Задание 26 № 339413
21.Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 17 и MB = 19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Решение.
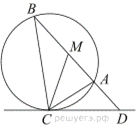
Угол 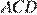 равен половине дуги на которую он опирается, поскольку это угол, образованный касательной к окружности и секущей, проведённой через точку касания. Угол
равен половине дуги на которую он опирается, поскольку это угол, образованный касательной к окружности и секущей, проведённой через точку касания. Угол  — вписанный, поэтому он также равен половине дуги, на которую опирается. Углы
— вписанный, поэтому он также равен половине дуги, на которую опирается. Углы  и
и 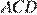 опираются на одну и ту же дугу, следовательно, они равны. Рассмотрим треугольники
опираются на одну и ту же дугу, следовательно, они равны. Рассмотрим треугольники 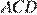 и
и 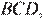 угол
угол 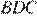 — общий, углы
— общий, углы  и
и 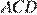 равны, следовательно, треугольники подобны, откуда
равны, следовательно, треугольники подобны, откуда 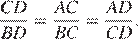 Биссектриса угла делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам:
Биссектриса угла делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам: 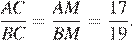 Получаем:
Получаем:
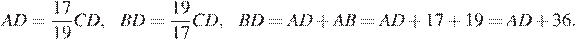
Найдём 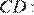
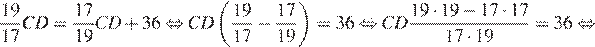
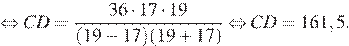
Ответ: 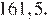
Критерии проверки:
Задание 26 № 311668
22.В треугольнике  угол
угол 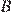 равен 120°, а длина стороны
равен 120°, а длина стороны 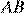 на
на 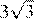 меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны
меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны 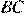 и продолжений сторон
и продолжений сторон 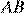 и
и 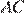 .
.
Решение.
Центр окружности является точкой пересечения биссектрис углов 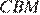 и
и 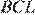 . При этом по свойству касательных
. При этом по свойству касательных 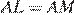 . Следовательно, длины ломаных
. Следовательно, длины ломаных 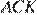 и
и 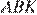 равны полупериметру
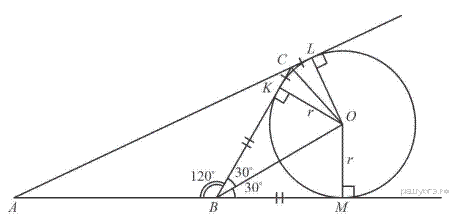
равны полупериметру 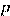 . По условию
. По условию 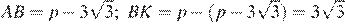 .
. 
Найдем радиус 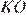 и<
и<
