Четырёхугольники и их элементы
Задание 25 № 77
1. 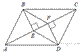 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
Решение.
 Прямоугольные треугольники ABE и CDF равны по гипотенузе и острому углу (AB = CD как противолежащие стороны параллелограмма; ∠BAE = ∠DCF как накрест лежащие углы при параллельных прямых AB и CD и секущей AC). Следовательно, BE = DF. Кроме того, BE || DF, т. к. это перпендикуляры к одной прямой. Таким образом, в четырёхугольнике BFDE противолежащие стороны равны и параллельны, поэтому BFDE — параллелограмм.
Прямоугольные треугольники ABE и CDF равны по гипотенузе и острому углу (AB = CD как противолежащие стороны параллелограмма; ∠BAE = ∠DCF как накрест лежащие углы при параллельных прямых AB и CD и секущей AC). Следовательно, BE = DF. Кроме того, BE || DF, т. к. это перпендикуляры к одной прямой. Таким образом, в четырёхугольнике BFDE противолежащие стороны равны и параллельны, поэтому BFDE — параллелограмм.
Критерии проверки:
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1301.
Задание 25 № 340935
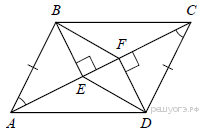
2.Сторона BC параллелограмма ABCD вдвое больше стороны CD. Точка L — середина стороны BC. Докажите, что DL — биссектриса угла CDA.
Решение.
 Проведём LF параллельно CD (см. рис.). Тогда BL = LC = CD. Следовательно, параллелограмм CDFL является ромбом. Диагональ DL ромба CDFL является биссектрисой угла CDA.
Проведём LF параллельно CD (см. рис.). Тогда BL = LC = CD. Следовательно, параллелограмм CDFL является ромбом. Диагональ DL ромба CDFL является биссектрисой угла CDA.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 26.11.2014 вариант МА90204.
Задание 25 № 340969
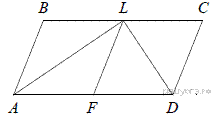
3.Сторона AB параллелограмма ABCD вдвое больше стороны BC. Точка N — середина стороны AB. Докажите, что CN — биссектриса угла BCD.
Решение.
 Проведём FN параллельно BC (см. рис.). Тогда AD = AN = NB. Следовательно, параллелограмм BCFN является ромбом. Диагональ CN ромба BCFN является биссектрисой угла BCD.
Проведём FN параллельно BC (см. рис.). Тогда AD = AN = NB. Следовательно, параллелограмм BCFN является ромбом. Диагональ CN ромба BCFN является биссектрисой угла BCD.
Критерии проверки:
Источник: СтатГрад: Диагностическая работа по математике 30.09.2014 вариант МА90101.
Задание 25 № 341286
4.В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
Решение.
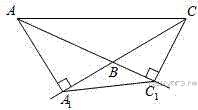
Поскольку угол ABC тупой, основания высот будут лежать на продолжениях сторон. Так как диагонали четырёхугольника AA1C1C пересекаются, он выпуклый, а поскольку 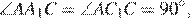 около него можно описать окружность. Тогда
около него можно описать окружность. Тогда 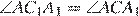 как вписанные углы, опирающиеся на дугу AA1, а
как вписанные углы, опирающиеся на дугу AA1, а  как вписанные углы, опирающиеся на дугу CC1. Значит, указанные треугольники подобны по двум углам.
как вписанные углы, опирающиеся на дугу CC1. Значит, указанные треугольники подобны по двум углам.
Критерии проверки:
Задание 25 № 341291
5.В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
Решение.

Поскольку угол ABC тупой, основания высот будут A1 и B1 лежать на продолжениях сторон BC и AC соответственно. Так как диагонали четырёхугольника AA1C1C пересекаются, он выпуклый, а поскольку 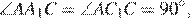 около четырёхугольника AA1C1C можно описать окружность. Тогда углы
около четырёхугольника AA1C1C можно описать окружность. Тогда углы 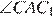 и
и 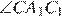 равны как вписанные углы, опирающиеся на дугу A1C1, Аналогично, равны углы
равны как вписанные углы, опирающиеся на дугу A1C1, Аналогично, равны углы 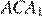 и
и 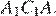 Значит, указанные треугольники подобны по двум углам.
Значит, указанные треугольники подобны по двум углам.
Критерии проверки:
Задание 25 № 341344
6.Биссектрисы углов C и D трапеции ABCD пересекаются в точке P, лежащей на стороне AB. Докажите, что точка P равноудалена от прямых BC, CD и AD.
Решение.
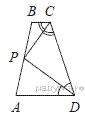 По свойству биссектрисы угла точка P равноудалена от прямых AD и CD (так как лежит на биссектрисе угла D ) и равноудалена от прямых BC и CD (так как лежит на биссектрисе угла C). Значит, точка P равноудалена от всех трёх указанных прямых.
По свойству биссектрисы угла точка P равноудалена от прямых AD и CD (так как лежит на биссектрисе угла D ) и равноудалена от прямых BC и CD (так как лежит на биссектрисе угла C). Значит, точка P равноудалена от всех трёх указанных прямых.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.04.2015 вариант МА90701.
Задание 25 № 341370
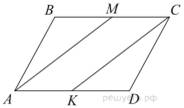
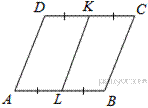
7.Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
Решение.
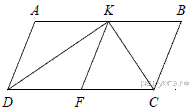 Проведём FK параллельно AD (см. рис.). Имеем AD = AK = KB, следовательно, параллелограмм AKFD является ромбом. Диагональ DK ромба AKFD является биссектрисой угла ADC.
Проведём FK параллельно AD (см. рис.). Имеем AD = AK = KB, следовательно, параллелограмм AKFD является ромбом. Диагональ DK ромба AKFD является биссектрисой угла ADC.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.04.2015 вариант МА90702.
Задание 25 № 341396
8.Точка K — середина боковой стороны CD трапеции ABCD. Докажите, что площадь треугольника KAB равна половине площади трапеции.
Решение.
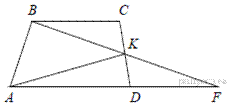 Продолжим BK до пересечения с прямой AD в точке F. Заметим, что в треугольниках FDK и BCK стороны CK и DK равны по условию, углы при вершине K равны как вертикальные, а углы KDF и KCB равны как накрест лежащие. Значит, треугольники FDK и BCK равны.
Продолжим BK до пересечения с прямой AD в точке F. Заметим, что в треугольниках FDK и BCK стороны CK и DK равны по условию, углы при вершине K равны как вертикальные, а углы KDF и KCB равны как накрест лежащие. Значит, треугольники FDK и BCK равны.
Следовательно, их площади равны, то есть площадь трапеции равна площади треугольника ABF. Но из равенства треугольников также вытекает, что FK = BK, то есть AK — медиана в треугольнике ABF. Тогда треугольник KAB по площади составит половину треугольника FAB, а значит, и данной трапеции.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.04.2015 вариант МА90703.
Задание 25 № 341511
9.Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.
Решение.
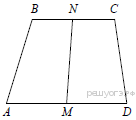 Пусть ABCD — трапеция, M и N — середины оснований AD и BC соответвенно.
Пусть ABCD — трапеция, M и N — середины оснований AD и BC соответвенно.
Пусть AM = MD = a и BN = NC = b, а h — высота трапеции. Тогда площадь каждой из частей, на которые отрезок MN делит трапецию, равна 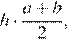 то есть, эти части равновелики.
то есть, эти части равновелики.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.05.2015 вариант МА90901.
Задание 25 № 341537
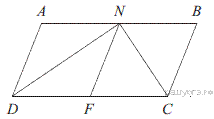
10.Сторона AD параллелограмма ABCD вдвое больше стороны CD. Точка M — середина стороны AD. Докажите, что CM — биссектриса угла BCD.
Решение.
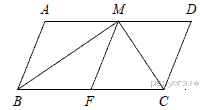 Проведём FM параллельно AB (см. рисунок). Тогда CD = AM = MD. Следовательно, параллелограмм DCFM является ромбом. Диагональ CM ромба DCFM является биссектрисой угла BCD.
Проведём FM параллельно AB (см. рисунок). Тогда CD = AM = MD. Следовательно, параллелограмм DCFM является ромбом. Диагональ CM ромба DCFM является биссектрисой угла BCD.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 07.05.2015 вариант МА90902.
Задание 25 № 155
11. 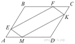
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Решение.
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, то треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма это четырехугольника- параллелограмм.
Критерии проверки:
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1313.
Задание 25 № 181
12.  Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Решение.
Вычислим угол восьмиугольника по формуле 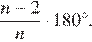 Таким образом, угол восьмиугольника равен
Таким образом, угол восьмиугольника равен 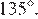 Если вершины последовательно соединить отрезками через одну, то образуются четыре равных равнобедренных треугольника, углы при основании которых равны
Если вершины последовательно соединить отрезками через одну, то образуются четыре равных равнобедренных треугольника, углы при основании которых равны 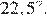 Тогда угол между двумя отрезками, которые соединяют вершины равен
Тогда угол между двумя отрезками, которые соединяют вершины равен 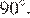 Поскольку все четыре равнобедренных треугольника равны, то и стороны получившегося четырёхугольника равны. Таким образом, если вершины восьмиугольника последовательно соединить отрезками через одну, то получится квадрат.
Поскольку все четыре равнобедренных треугольника равны, то и стороны получившегося четырёхугольника равны. Таким образом, если вершины восьмиугольника последовательно соединить отрезками через одну, то получится квадрат.
Критерии проверки:
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1317.
Задание 25 № 315039
13.  Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Решение.
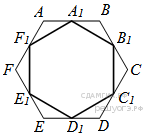 Рассмотрим маленькие треугольники
Рассмотрим маленькие треугольники 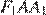 и
и 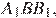
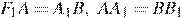 ,
, 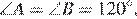 следовательно, эти треугольники равны по двум сторонам и углу. Аналогично равны между собой и остальные маленькие треугольники. Следовательно
следовательно, эти треугольники равны по двум сторонам и углу. Аналогично равны между собой и остальные маленькие треугольники. Следовательно 
Любой угол правильного шестиугольника равен 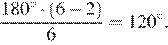 Треугольники
Треугольники 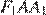 и
и 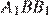 — равнобедренные, углы при основаниях равны
— равнобедренные, углы при основаниях равны  Рассмотрим развёрнутый угол
Рассмотрим развёрнутый угол 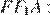
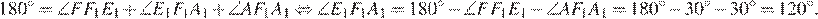
Аналогично все остальные углы шестиугольника 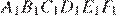 равны
равны 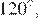 следовательно шестиугольник
следовательно шестиугольник 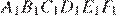 — правильный.
— правильный.
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 25 № 51
14.В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник.
Решение.
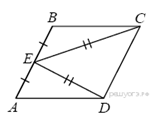
Треугольники BEC и AED равны по трём сторонам. Значит, углы CBE и DAE равны. Так как их сумма равна 180°, то углы равны 90°. Такой параллелограмм — прямоугольник.
Критерии проверки:
Источник: Демонстрационная версия ГИА—2013 по математике.
Задание 25 № 311663
15. 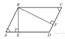 В параллелограмме
В параллелограмме 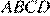 проведены высоты
проведены высоты 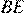 и
и 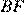 . Докажите, что
. Докажите, что 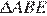 подобен
подобен 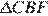 .
.
Решение.
В треугольниках 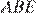 и
и 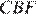 имеем
имеем 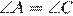 как противоположные углы параллелограмма,
как противоположные углы параллелограмма,  как прямые углы, значит треугольники подобны по первому признаку подобия треугольников.
как прямые углы, значит треугольники подобны по первому признаку подобия треугольников.
Критерии проверки:
Источник: ГИА-2013. Математика. Тренировочная работа №1 (3 вар.)
Задание 25 № 311573
16.  В параллелограмме
В параллелограмме 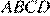 проведены высоты
проведены высоты 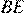 и
и 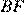 . Докажите, что
. Докажите, что 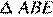 подобен
подобен 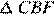 .
.
Решение.
В треугольниках 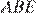 и
и 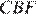 имеем
имеем 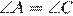 как противоположные углы параллелограмма,
как противоположные углы параллелограмма,  как прямые углы, значит треугольники подобны по первому признаку подобия треугольников.
как прямые углы, значит треугольники подобны по первому признаку подобия треугольников.
Критерии проверки:
Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)
Задание 25 № 311604
17. 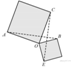 Два квадрата имеют общую вершину. Докажите, что отмеченные на рисунке отрезки
Два квадрата имеют общую вершину. Докажите, что отмеченные на рисунке отрезки 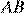 и
и 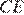 равны.
равны.
Решение.
Пусть общая вершина квадратов — точка 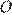 .
. 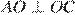 и
и 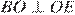 . Следовательно,
. Следовательно, 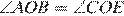 . Тогда треугольники
. Тогда треугольники 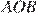 и
и 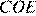 равны по двум сторонам и углу между ними. Следовательно,
равны по двум сторонам и углу между ними. Следовательно, 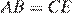 как соответствующие стороны равных треугольников.
как соответствующие стороны равных треугольников.
Критерии проверки:
Источник: ГИА-2012. Математика. Диагностическая работа № 2(1вар)
Задание 25 № 311603
18.В параллелограмме проведены биссектрисы противоположных углов. Докажите, что отрезки биссектрис, заключенные внутри параллелограмма, равны.
Решение.
 — параллелограмм
— параллелограмм
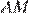 — биссектриса
— биссектриса 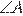 ,
, 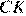 — биссектриса
— биссектриса 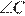 .
.
Докажите, что 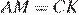 .
.
1) 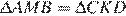 по стороне и двум прилежащим к ней углам:
по стороне и двум прилежащим к ней углам:
а)  — по свойству противоположных сторон параллелограмма;
— по свойству противоположных сторон параллелограмма;
б)  по свойству противоположных углов параллелограмма;
по свойству противоположных углов параллелограмма;
в)  по определению биссектрисы и равенству противоположных углов параллелограмма.
по определению биссектрисы и равенству противоположных углов параллелограмма.
2)  как соответствующие элементы равных треугольников.
как соответствующие элементы равных треугольников.
Критерии проверки:
Источник: ГИА-2012. Математика. Диагностическая работа № 1(2 вар)
Задание 25 № 311608
19.Середины сторон параллелограмма является вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.
Решение.
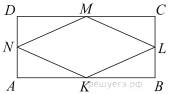
Пусть точки 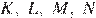 — середины сторон
— середины сторон 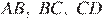 и
и 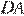 параллелограмма
параллелограмма 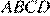 соответственно
соответственно
1)  т. к.
т. к. 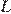 — середина
— середина 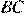 ;
;
2) 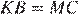 , т. к.
, т. к.  как противоположные стороны параллелограмма, а
как противоположные стороны параллелограмма, а 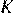 и
и 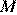 — середины этих сторон;
— середины этих сторон;
3)  как стороны ромба.
как стороны ромба.
Тогда треугольники 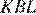 и
и 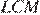 равны по трем сторонам. Это означает, что угол
равны по трем сторонам. Это означает, что угол 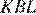 равен углу
равен углу 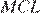 . Но эти углы в сумме дают 180°, поэтому каждый из них равен 90°. Таким образом, углы параллелограмма прямые. Значит, он прямоугольник.
. Но эти углы в сумме дают 180°, поэтому каждый из них равен 90°. Таким образом, углы параллелограмма прямые. Значит, он прямоугольник.
Критерии проверки:
Источник: ГИА-2012. Математика. Тренировочная работа № 2(1 вар)
Задание 25 № 311607
20.Дана равнобедренная трапеция 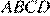 . Точка
. Точка 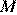 лежит на основании
лежит на основании 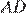 и равноудалена от концов другого основания. Докажите, что
и равноудалена от концов другого основания. Докажите, что 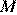 — середина основания
— середина основания 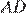 .
.
Решение.
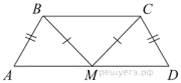
Треугольник 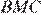 равнобедренный. Поэтому
равнобедренный. Поэтому  . В равнобедренной трапеции
. В равнобедренной трапеции  .
.
Отсюда следует, что 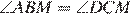 . Значит, треугольники
. Значит, треугольники 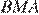 и
и 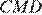 равны по двум сторонам и углу между ними. Следовательно,
равны по двум сторонам и углу между ними. Следовательно,  .
.
Критерии проверки:
Источник: ГИА-2012. Математика. Тренировочная работа №1 (1 вар.)
Задание 25 № 311667
21.Три стороны параллелограмма равны. Докажите, что отрезок с концами в серединах противоположных сторон параллелограмма равен четверти его периметра.
Решение.
 В параллелограмме противоположные стороны равны, поэтому если равны три стороны, то все стороны этого параллелограмма равны, значит, это ромб. Отрезки
В параллелограмме противоположные стороны равны, поэтому если равны три стороны, то все стороны этого параллелограмма равны, значит, это ромб. Отрезки 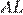 и
и 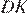 равны и параллельны, следовательно,
равны и параллельны, следовательно, 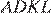 — параллелограмм, значит, длина
— параллелограмм, значит, длина 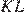 равна длине стороны
равна длине стороны 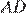 и, следовательно, равна четверти периметра параллелограмма.
и, следовательно, равна четверти периметра параллелограмма.
Критерии проверки:
Источник: ГИА-2013. Математика. Тренировочная работа № 4.(1 вар.)
Задание 25 № 311925
22.В параллелограмме ABCD проведены высоты BH и BE к сторонам AD и CD соответственно, при этом BH = BE. Докажите, что ABCD — ромб.
Решение.
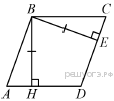
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
Тогда, с одной стороны, S = AD · BH, а с другой стороны, S = CD · BE. Поскольку BH = BE , получаем, что AD = CD. Следовательно, все стороны параллелограмма равны, а значит, ABCD — ромб.
Критерии проверки:
Источник: МИОО: Тренировочная работа по математике 19.11.2013 вариант МА90201.
Задание 25 № 314822
23.В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.Решение.
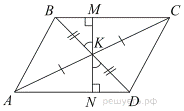
Проведём высоту 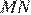 так, чтобы она проходила через точку
так, чтобы она проходила через точку 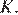 Углы
Углы 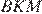 и
и 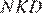 равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно,
равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно,  Рассмотрим треугольники
Рассмотрим треугольники 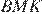 и
и 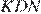 , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки
, они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки 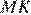 и
и 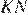 . Таким образом,
. Таким образом, 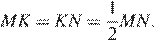
Площадь параллелограмм равна 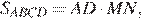 а площадь треугольника
а площадь треугольника 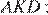
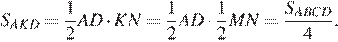
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 25 № 315047
24.  Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Решение.
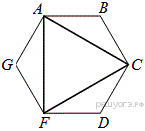 Рассмотрим треугольники
Рассмотрим треугольники 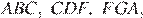

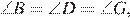 следовательно эти треугольники равны по двум сторонам и углу между ними, значит,
следовательно эти треугольники равны по двум сторонам и углу между ними, значит, 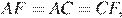 то есть треугольник
то есть треугольник 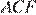 — правильный.
— правильный.
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 25 № 315120
25.  Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Решение.
 Рассмотрим треугольники
Рассмотрим треугольники 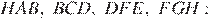

следовательно эти треугольники равны, то есть 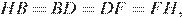 следовательно
следовательно 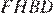 — ромб.
— ромб.
Любой угол правильного восьмиугольника равен 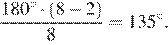 Каждый их треугольников
Каждый их треугольников 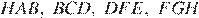 — равнобдеренный, следовательно углы при основании этих треугольников равны
— равнобдеренный, следовательно углы при основании этих треугольников равны 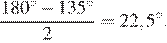
Рассмотрим угол 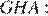
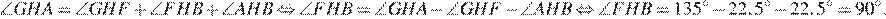
Следовательно все углы, в ромбе 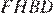 — прямые, а значит,
— прямые, а значит, 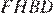 — квадрат.
— квадрат.
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 25 № 315124
26.  Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Решение.
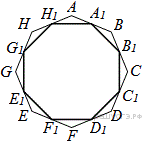 Рассмотрим маленькие треугольники
Рассмотрим маленькие треугольники 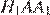 и
и 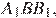
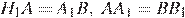 ,
, 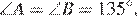 следовательно, эти треугольники равны по двум сторонам и углу. Аналогично равны между собой и остальные маленькие треугольники. Следовательно
следовательно, эти треугольники равны по двум сторонам и углу. Аналогично равны между собой и остальные маленькие треугольники. Следовательно 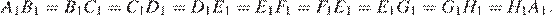
Любой угол правильного восьмиугольника равен 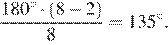 Треугольники
Треугольники 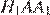 и
и 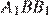 — равнобедренные, углы при основаниях равны
— равнобедренные, углы при основаниях равны 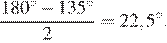 Рассмотрим развёрнутый угол
Рассмотрим развёрнутый угол 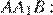
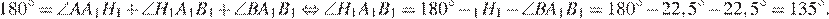
Аналогично все остальные углы восьмиугольника  равны
равны 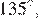 следовательно восьмиугольник
следовательно восьмиугольник  — правильный.
— правильный.
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 25 № 333026
27.Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции.
Решение.
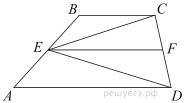
Проведём отрезок EF параллельно основаниям трапеции, точка F лежит на стороне CD. Отрезок EF — средняя линия трапеции ABCD, значит, высоты треугольников EFD и CEF , проведённые к стороне EF , равны между собой и равны половине высоты трапеции h. Имеем
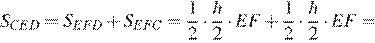
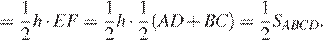
Критерии проверки:
Источник: МИОО: Диагностическая работа по математике 17.04.2014 вариант МА90601
Задание 25 № 333131
28.Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Решение.
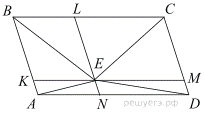
Проведём через точку 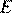 прямые, параллельные сторонам параллелограмма, пересекающие его стороны AB, BC , CD иAD в точкахK , L, M иN соответственно. Эти прямые делят параллелограммABCD на четыре параллелограмма. Поскольку диагональ делит параллелограмм на два равных треугольника, получаем
прямые, параллельные сторонам параллелограмма, пересекающие его стороны AB, BC , CD иAD в точкахK , L, M иN соответственно. Эти прямые делят параллелограммABCD на четыре параллелограмма. Поскольку диагональ делит параллелограмм на два равных треугольника, получаем
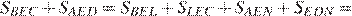
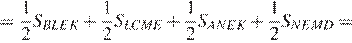

Критерии проверки:
Источник: МИОО: Диагностическая работа по математике 17.04.2014 вариант МА90605
Задание 25 № 333322
29.Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Решение.
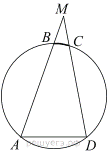
Поскольку четырёхугольник ABCD вписанный, сумма углов BAD и BCD равна 180°.
Следовательно,
∠MCB = 180° − ∠BCD = ∠BAD.
Получаем, что в треугольниках MBC и MDA углы MCB и MAD равны, угол M общий, следовательно, эти треугольники подобны.
Критерии проверки:
Источник: МИОО: Тренировочная работа по математике 06.05.2014 вариант МА90701.
Задание 25 № 339506
30.Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD = 10. Докажите, что треугольники CBD и ADB подобны.
Решение.
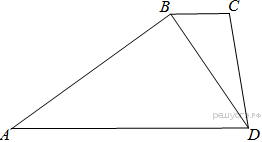 Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках 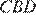 и
и 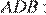
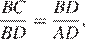 следовательно, эти треугольники подобны по двум парам подобных сторон и углу между ними.
следовательно, эти треугольники подобны по двум парам подобных сторон и углу между ними.
Критерии проверки:
Задание 25 № 339602
31.Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции.
Решение.
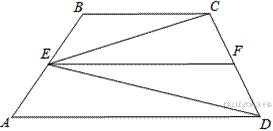 Проведём построения и введём обозначения как указано на рисунке. Проведём
Проведём построения и введём обозначения как указано на рисунке. Проведём 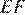 параллельно
параллельно 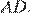 Поскольку
Поскольку 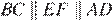 и
и 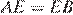 по теореме Фаллеса получаем, что
по теореме Фаллеса получаем, что 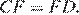 Следовательно,
Следовательно, 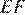 — средняя линия. Пусть
— средняя линия. Пусть 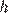 — длина высоты трапеции. Площадь трапеции равна:
— длина высоты трапеции. Площадь трапеции равна:
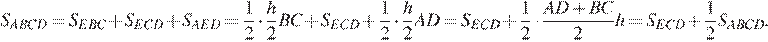
Откуда получаем, что 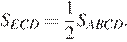
Критерии проверки:
Задание 25 № 339609
32.Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
Решение.
В задаче возможны два случая.
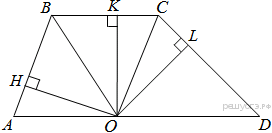 Первый случай, AD — одно из оснований. Проведём построения и введём обозначения как указано на рисунке. Рассмотрим треугольники OBH и BOK Рассмотрим треугольники OBH и OBK, они прямоугольные, углы HBO и KBO равны, OB — общая, следовательно, треугольники равны. Откуда OH = OK. Аналогично из треугольников KOC и COL получаем, что OK = OL. Таким образом, OH = OK = OL.
Первый случай, AD — одно из оснований. Проведём построения и введём обозначения как указано на рисунке. Рассмотрим треугольники OBH и BOK Рассмотрим треугольники OBH и OBK, они прямоугольные, углы HBO и KBO равны, OB — общая, следовательно, треугольники равны. Откуда OH = OK. Аналогично из треугольников KOC и COL получаем, что OK = OL. Таким образом, OH = OK = OL.
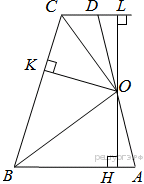 Второй случай, AD — одна из боковых сторон. Несмотря на другую геометрическую конфигурацию, доказательство полностью повторяет доказательство для первого случая.
Второй случай, AD — одна из боковых сторон. Несмотря на другую геометрическую конфигурацию, доказательство полностью повторяет доказательство для первого случая.
Критерии проверки:
Задание 25 № 339625
33.В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD также равны.
Решение.
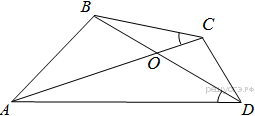 Проведём построения и введём обозначения как показано на рисунке. Рассмотрим треугольники
Проведём построения и введём обозначения как показано на рисунке. Рассмотрим треугольники 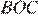 и
и 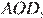 углы
углы 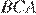 и
и 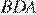 равны по условию, углы
равны по условию, углы 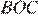 и
и 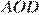 равны как вертикальные, следовательно, треугольники
равны как вертикальные, следовательно, треугольники 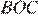 и
и 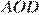 подобны. Откуда
подобны. Откуда 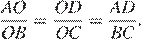 Равенство
Равенство  можно представить в виде
можно представить в виде 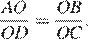 Рассмотрим треугольники
Рассмотрим треугольники 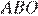 и
и 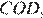 углы
углы 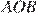 и
и 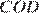 равны как вертикальные и имеется равенство
равны как вертикальные и имеется равенство 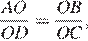 следовательно, треугольники подобны. Поэтому углы
следовательно, треугольники подобны. Поэтому углы 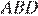 и
и  равны.
равны.
Критерии проверки:
Задание 25 № 340055
34.В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O. Докажите, что площади треугольников AOB и COD равны.
Решение.
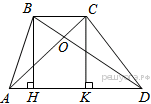 Проведём высоты
Проведём высоты  и
и  они равны. Площадь треугольника
они равны. Площадь треугольника 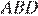 равна
равна 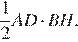 Площадь треугольника
Площадь треугольника 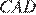 равна
равна 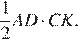 Поскольку высоты
Поскольку высоты 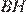 и
и 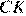 равны, равны и площади треугольников
равны, равны и площади треугольников 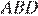 и
и 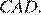 Покажем, что площади треугольников
Покажем, что площади треугольников 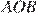 и
и 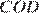 равны:
равны:
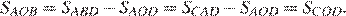
Критерии проверки:
Задание 25 № 340104
35.Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках P и T соответственно. Докажите, что BP = DT.
Решение.
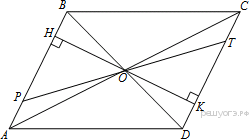 Проведём через точку
Проведём через точку 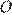 прямую
прямую 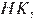 перпендикулярную стороне
перпендикулярную стороне 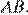 Поскольку стороны
Поскольку стороны 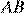 и
и 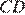 параллельны,
параллельны, 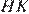 также перпендикулярно и стороне
также перпендикулярно и стороне 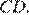 Диагонали параллелограмма точкой пересечения делятся пополам. Рассмотрим треугольники
Диагонали параллелограмма точкой пересечения делятся пополам. Рассмотрим треугольники 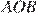 и
и 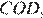
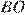 равно
равно 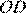 ,
, 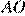 равно
равно 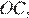 углы
углы 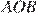 и
и 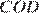 равны как вертикальные, следовательно, треугольники равны. Поэтому равны их соответствующие элементы, то есть
равны как вертикальные, следовательно, треугольники равны. Поэтому равны их соответствующие элементы, то есть  Рассмотрим треугольники
Рассмотрим треугольники 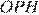 и
и 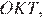 они прямоугольные,
они прямоугольные, 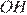 равно
равно 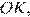 углы
углы 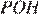 и
и 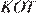 равны как вертикальные, следовательно, треугольники равны, поэтому
равны как вертикальные, следовательно, треугольники равны, поэтому 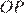 равно
равно 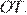 Рассмот<
Рассмот<
