Геометрическая задача на доказательство
Треугольники
Четырехугольники
Окружность
Треугольники и их элементы
Задание 25 № 103
1. 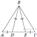 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
Решение.
Так как по условию  то треугольник
то треугольник 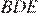 является равнобедренным. Пусть угол при основании этого треугольника равен x, тогда
является равнобедренным. Пусть угол при основании этого треугольника равен x, тогда 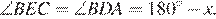 Треугольники
Треугольники 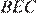 и
и 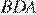 равны по двум сторонам и углу между ними, поэтому
равны по двум сторонам и углу между ними, поэтому 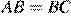 и треугольник
и треугольник  —равнобедренный.
—равнобедренный.
Критерии проверки:
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1305.
Задание 25 № 340341
2.Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
Решение.
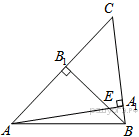 Рассмотрим треугольники
Рассмотрим треугольники 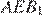 и
и 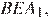 они прямоугольные, углы
они прямоугольные, углы 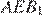 и
и 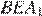 равны как вертикальные, следовательно, треугольники подобны, откуда
равны как вертикальные, следовательно, треугольники подобны, откуда 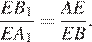 Рассмотрим треугольники
Рассмотрим треугольники 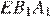 и
и 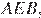 углы
углы 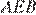 и
и 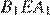 равны как вертикальные,
равны как вертикальные, 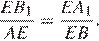 следовательно, эти треугольники подобны, откуда
следовательно, эти треугольники подобны, откуда 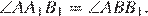
См. также.
Аналогичное задание с тупоугольным треугольником: 340854.
Критерии проверки:
Задание 25 № 340854
3.В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
Решение.
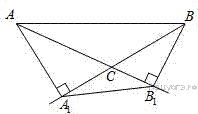
Поскольку угол ACB тупой, основания высот A1 и B1 будут лежать на продолжениях сторон BC и AC соответственно. Диагонали четырёхугольника AA1B1B пересекаются, поэтому он выпуклый. Поскольку ∠AA1B = ∠AB1B = 90°, каждый из прямоугольных треугольников AA1B и AB1B вписан в окружность с диаметром AB. Это означает, что все вершины четырёхугольника AA1B1B лежат на одной окружности. Тогда углы ∠AB1A1 и ∠ABA1 равны как вписанные углы, опирающиеся на дугу A1A. Аналогично, ∠BA1B1 = ∠BAB1. Значит, указанные треугольники подобны по двум углам.
Укажем общую теорему.
Основания двух высот треугольника (остроугольного или тупоугольного) и одна из его вершин образуют треугольник, подобный исходному; коэффициент подобия равен модулю косинуса их общего угла.
См. также.
Аналогичное задание с остроугольным треугольником: 340341.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 26.11.2014 вариант МА90201.
Задание 25 № 340880
4.В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
Решение.
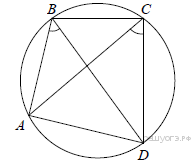 Поскольку ABCD выпуклый и ∠ABD = ∠ACD, получаем, что около четырёхугольника ABCD можно описать окружность. А тогда ∠DAC = ∠DBC как вписанные углы, опирающиеся на одну дугу CD.
Поскольку ABCD выпуклый и ∠ABD = ∠ACD, получаем, что около четырёхугольника ABCD можно описать окружность. А тогда ∠DAC = ∠DBC как вписанные углы, опирающиеся на одну дугу CD.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 26.11.2014 вариант МА90202.
Задание 25 № 340906
5.Окружности с центрами в точках E и F пересекаются в точках C и D, причём точки E и F лежат по одну сторону от прямой CD. Докажите, что CD ⊥ EF.
Решение.
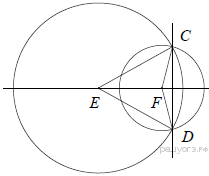 Точка E равноудалена от C и D , поэтому она лежит на серединном перпендикуляре к отрезку CD. То же можно сказать и о F. Значит EF — серединный перпендикуляр к CD, то есть CD ⊥ EF.
Точка E равноудалена от C и D , поэтому она лежит на серединном перпендикуляре к отрезку CD. То же можно сказать и о F. Значит EF — серединный перпендикуляр к CD, то есть CD ⊥ EF.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 26.11.2014 вариант МА90203.
Задание 25 № 341688
6.Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
Решение.
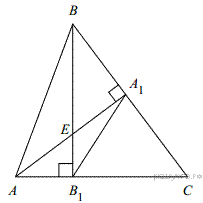
Поскольку диагонали четырехугольника AB1A1B пересекаются, он является выпуклым, а так как 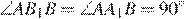 , около него можно описать окружность. Тогда углы AA1B1 и ABB1 равны как вписанные, опирающиеся на одну дугу AB1.
, около него можно описать окружность. Тогда углы AA1B1 и ABB1 равны как вписанные, опирающиеся на одну дугу AB1.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 29.09.2015 вариант МА90103.
Задание 25 № 129
7. 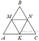 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
Решение.
Так как точки M, N, K - середины сторон и треугольник ABC- равносторонний, то отрезки AM, MB, BN, NC, KC, AK равны. В равностороннем треугольнике все углы равны, таким образом, треугольники AMK, NMB, CNK равны по двум сторонам и углу между ними. Тогда MN=MK=KN, значит треугольник MNK- равносторонний.
Критерии проверки:
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1309.
Задание 25 № 311561
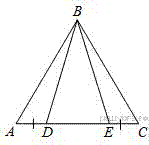
8.На стороне 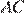 треугольника
треугольника  отмечены точки
отмечены точки 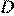 и
и 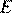 так, что
так, что 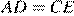 . Докажите, что если
. Докажите, что если 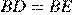 , то
, то 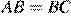 .
.
Решение.
Треугольник 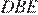 — равнобедренный, поэтому
— равнобедренный, поэтому 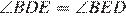 . Значит,
. Значит,  и треугольники
и треугольники 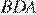 и
и 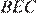 равны по первому признаку равенства треугольников. Значит,
равны по первому признаку равенства треугольников. Значит, 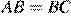 .
.
Критерии проверки:
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)
Задание 25 № 311567
9.На медиане 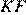 треугольника
треугольника 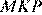 отмечена точка
отмечена точка 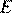 . Докажите, что если
. Докажите, что если 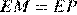 , то
, то 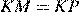 .
.
Решение.
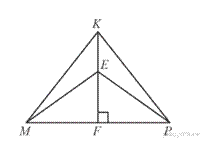
Поскольку треугольник 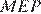 — равнобедренный, получаем, что его медиана
— равнобедренный, получаем, что его медиана 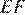 также является высотой. Значит, в треугольнике
также является высотой. Значит, в треугольнике 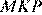 отрезок
отрезок 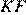 является высотой и медианой. Поэтому треугольник
является высотой и медианой. Поэтому треугольник 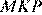 — равнобедренный, то есть
— равнобедренный, то есть 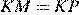 .
.
Критерии проверки:
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
Задание 25 № 311602
10.Докажите, что биссектрисы углов при основании равнобедренного треугольника равны.
Решение.
Имеем: 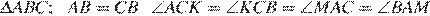
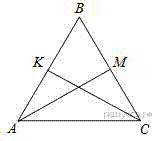
Докажем, что 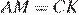 .
.
1) 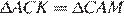 по стороне и двум прилежащим к ней углам:
по стороне и двум прилежащим к ней углам:
а) 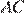 — общая;
— общая;
б) 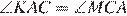 по свойству углов равнобедренного треугольника;
по свойству углов равнобедренного треугольника;
в) 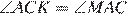 по определению биссектрисы и равенству углов при основании равнобедренного треугольника.
по определению биссектрисы и равенству углов при основании равнобедренного треугольника.
2)  как соответствующие элементы равных треугольников.
как соответствующие элементы равных треугольников.
Критерии проверки:
Источник: ГИА-2012. Математика. Диагностическая работа № 1 (1 вар)
Задание 25 № 311605
11. 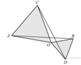 Два равносторонних треугольника имеют общую вершину. Докажите, что отмеченные на рисунке отрезки
Два равносторонних треугольника имеют общую вершину. Докажите, что отмеченные на рисунке отрезки 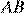 и
и 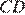 равны.
равны.
Решение.
Рассмотрим треугольники 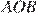 и
и 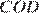 .
.
В них 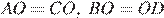 и
и
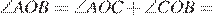 60°
60° 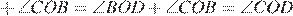 .
.
Следовательно, эти треугольники равны по двум сторонам и углу между ними.
Поэтому  как соответствующие стороны равных треугольников.
как соответствующие стороны равных треугольников.
Критерии проверки:
Источник: ГИА-2012. Математика. Диагностическая работа №2 (2 вар.)
Задание 25 № 311606
12. 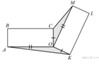 Два равных прямоугольника имеют общую вершину
Два равных прямоугольника имеют общую вершину 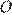 (см. рис.). Докажите, что площади треугольников
(см. рис.). Докажите, что площади треугольников 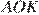 и
и 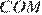 равны.
равны.
Решение.
Две стороны одного треугольника соответственно равны двум сторонам другого:  и
и  . Рассмотрим углы между ними:
. Рассмотрим углы между ними:
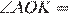 360°
360° 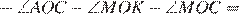 180°
180° 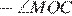 .
.
Поэтому
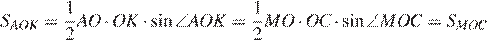 .
.
Критерии проверки:
Источник: ГИА-2012. Математика. Диагностическая работа №2 (3 вар.)
Задание 25 № 311665
13.Докажите, что у равных треугольников  и
и 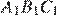 биссектрисы, проведённые из вершины
биссектрисы, проведённые из вершины 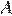 и
и 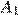 , равны.
, равны.
Решение.
Пусть 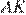 и
и 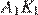 — биссектрисы треугольников
— биссектрисы треугольников  и
и 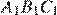 . В треугольниках
. В треугольниках 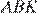 и
и 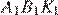 соответственно равны стороны
соответственно равны стороны 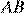 и
и 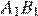 , а также углы
, а также углы 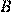 и
и 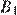 ,
, 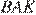 и
и 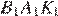 . Следовательно, треугольники равны по второму признаку равенства треугольников. Значит,
. Следовательно, треугольники равны по второму признаку равенства треугольников. Значит, 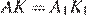 , что и требовалось доказать.
, что и требовалось доказать. 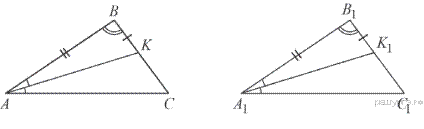
Критерии проверки:
Источник: ГИА-2013. Математика. Тренировочная работа №2.(4 вар)
Задание 25 № 311669
14.В треугольнике  угол
угол 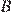 равен 36°,
равен 36°, 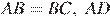 — биссектриса. Докажите, что треугольник
— биссектриса. Докажите, что треугольник 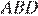 — равнобедренный.
— равнобедренный.
Решение.
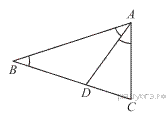 Треугольник
Треугольник  равнобедренный, поэтому
равнобедренный, поэтому 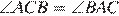 = 72°. Значит,
= 72°. Значит, 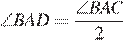 = 36°. Таким образом, углы
= 36°. Таким образом, углы 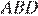 и
и 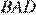 равны, поэтому треугольник
равны, поэтому треугольник 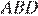 — равнобедренный.
— равнобедренный.
Критерии проверки:
Источник: ГИА-2013. Математика. Пробные варианты от ФИПИ (1 вар.)
Задание 25 № 311773
15.В остроугольном треугольнике ABC угол B равен 60°. Докажите, что точки A, C, центр описанной окружности треугольника ABC и точка пересечения высот треугольника ABC лежат на одной окружности.
Решение.
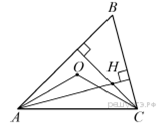
Обозначим центр описанной окружности треугольника ABC черезO, а точку пересечения высот через H. Тогда 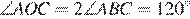 и
и 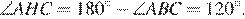 Таким образом, точки A, C, O и H лежат на одной окружности.
Таким образом, точки A, C, O и H лежат на одной окружности.
Критерии проверки:
Источник: МИОО: Диагностическая работа по математике 01.10.2013 вариант МА90101.
Задание 25 № 311969
16.Окружность касается стороны AB треугольника ABC, у которого ∠C = 90°, и продолжений его сторон AC и BC за точки A и B соответственно. Докажите, что периметр треугольника ABC равен диаметру этой окружности.
Решение.
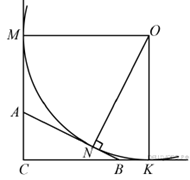
Пусть O — центр окружности, d — её диаметр, а M, N и K — точки касания окружности с прямыми AC, AB и BC соответственно. Радиус OM перпендикулярен AC, а OK перпендикулярен BC. Следовательно, в четырёхугольнике OMCK имеем ∠C = ∠M = ∠K = 90°, а значит, OMCK — прямоугольник. Поскольку OM = OK, прямоугольник OMCK — квадрат. Следовательно, 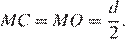
Отрезки касательных, проведённых из одной точки к окружности, равны: AM = AN, BN = BK и CM = CK. Периметр треугольника ABC равен
P = AB + BC + AC = AC + AN + BN + BC =
= AC + AM + BK + BC = MC + CK = 2MC = d.
Критерии проверки:
Источник: МИОО: Тренировочная работа по математике 19.11.2013 вариант МА90202.
Задание 25 № 315062
17. 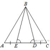 На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
Решение.
Углы 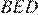 и
и 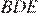 равны, поэтому треугольник
равны, поэтому треугольник 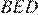 — равнобедренный, то есть
— равнобедренный, то есть 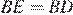
Углы 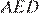 и
и 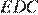 — развёрнутые, поэтому:
— развёрнутые, поэтому:
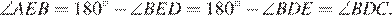
Рассмотрим треугольники 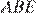 и
и 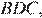
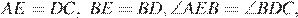 следовательно, эти треугольники равны, а значит,
следовательно, эти треугольники равны, а значит,  то есть треугольник
то есть треугольник  — равнобедренный.
— равнобедренный.
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 25 № 315085
18. 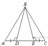 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
Решение.
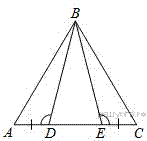
Углы 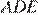 и
и 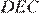 — развёрнутые, поэтому:
— развёрнутые, поэтому:
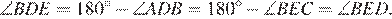
Углы 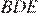 и
и 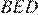 равны, следовательно, треугольник
равны, следовательно, треугольник 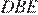 — равнобедренный, значит
— равнобедренный, значит 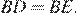
Рассмотрим треугольники 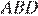 и
и 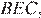
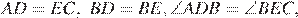 следовательно, эти треугольники равны, а значит,
следовательно, эти треугольники равны, а значит,  то есть треугольник
то есть треугольник  — равнобедренный.
— равнобедренный.
Критерии проверки:
Источник: Банк заданий ФИПИ
Задание 25 № 316244
19.В остроугольном треугольнике ABC точки A, C, центр описанной окружности O и центр вписанной окружности I лежат на одной окружности. Докажите, что угол ABC равен 60°.
Решение.
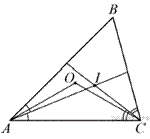 В треугольнике ABC имеем
В треугольнике ABC имеем 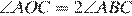 , а
, а 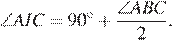
Таким образом, 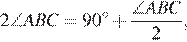 значит,
значит, 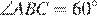
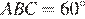
Критерии проверки:
Источник: Диагностическая работа 01.10.2013 Вариант МА90105
Задание 25 № 316334
20.В остроугольном треугольнике ABC угол B равен 60° . Докажите, что точки A, C, центр описанной окружности треугольника ABC и центр вписанной окружности треугольника ABC лежат на одной окружности.
Решение.
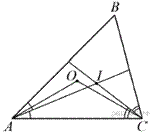 Обозначим центр описанной окружности треугольника ABC через O, а центр вписанной окружности через I.
Обозначим центр описанной окружности треугольника ABC через O, а центр вписанной окружности через I.
Тогда
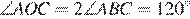
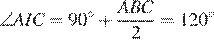
Таким образом, точки A, C, O и I лежат на одной окружности.
Критерии проверки:
Источник: МИОО: Диагностическая работа по математике 01.10.2013 вариант МА90103.
Задание 25 № 333348
21.Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
Решение.
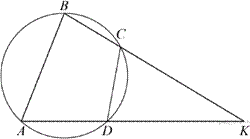 Поскольку четырёхугольник ABCD вписанный, сумма углов ABC и ADC равна 180°.
Поскольку четырёхугольник ABCD вписанный, сумма углов ABC и ADC равна 180°.
Следовательно,
∠KDC =180° − ∠ADC = ∠ABC.
Получаем, что в треугольниках KAB и KCD углы ABK и CDK равны, угол K общий, следовательно, эти треугольники подобны.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 26.11.2014 вариант МА90702.
Задание 25 № 339384
22.Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Решение.
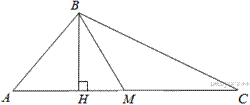 Введём обозначения как показано на рисунке. Проведём медиану
Введём обозначения как показано на рисунке. Проведём медиану 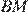 и высоту
и высоту 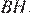 Площадь треугольника
Площадь треугольника 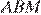
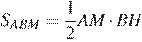 , площадь треугольника
, площадь треугольника 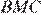
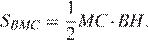 Отрезки
Отрезки 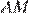 и
и 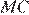 равны, следовательно,
равны, следовательно, 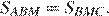
Критерии проверки:
Задание 25 № 340243
23.В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
Решение.
Углы 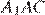 и
и 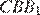 равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники
равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники 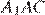 и
и 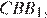 они прямоугольные, углы
они прямоугольные, углы 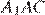 и
и 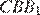 равны, следовательно, эти треугольники подобны, откуда
равны, следовательно, эти треугольники подобны, откуда 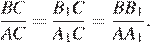 Рассмотрим треугольники
Рассмотрим треугольники 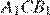 и
и 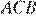 углы
углы 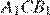 и
и 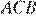 равны как вертикальные,
равны как вертикальные, 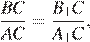 следовательно, эти треугольники подобны.
следовательно, эти треугольники подобны.
Критерии проверки:
Задание 25 № 349266
24.Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
Решение.
 Поскольку четырёхугольник ABCD вписанный, сумма углов ABC и ADC равна 180°.
Поскольку четырёхугольник ABCD вписанный, сумма углов ABC и ADC равна 180°.
Следовательно,
∠KDC =180° − ∠ADC = ∠ABC.
Получаем, что в треугольниках KAB и KCD углы ABK и CDK равны, угол K общий, следовательно, эти треугольники подобны.
----------
Дублирует задание 333348
Задание 25 № 350829
25.В треугольнике ABC с тупым углом BAC проведены высоты BB1 и CC1. Докажите, что треугольники AB1C1 и ABC подобны.
Решение.
Углы 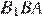 и
и 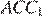 равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники
равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники 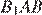 и
и 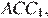 они прямоугольные, углы
они прямоугольные, углы 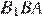 и
и 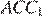 равны, следовательно, эти треугольники подобны, откуда
равны, следовательно, эти треугольники подобны, откуда 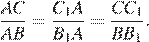 Рассмотрим треугольники
Рассмотрим треугольники 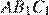 и
и  углы
углы 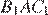 и
и 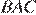 равны как вертикальные,
равны как вертикальные,  следовательно, эти треугольники подобны.
следовательно, эти треугольники подобны.
Задание 25 № 353162
26.В остроугольном треугольнике  проведены высоты
проведены высоты 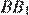 и
и 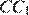 . Докажите, что углы
. Докажите, что углы 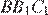 и
и 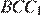 равны.
равны.
