Приближенные развертки развертывающихся поверхностей

Развертки, которые выполняются графически, являются приближенными

Поверхность аппроксимируется вписанным или описанным многогранником с гранями в виде треугольников или четырехугольников

Развертку боковой поверхности прямого кругового конусазаменяют разверткой боковой поверхности прямой правильной многоугольной пирамиды, вписанной в конус.

Построим развертку боковой поверхности кругового конуса, усеченного плоскостью α.

Делим основание конуса на 12 частей и проводим через точки деления образующие конуса, находим точки их пересечения с плоскостью α.

Изображение развертки обозначается специальным знаком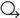

Из произвольной точки S на свободном поле чертежа проводим дугу радиусом, равным длине образующей конуса.

Засекаем последовательно от произвольной точки 1 двеннадцать дуг, хорды которых равны стороне 12-угольника, вписанного в основание конуса.

Проводим образующие конуса. На каждой образующей развертки откладываем натуральную величинудлины отрезка соответствующей образующей конуса от его вершины до точки пересечения с плоскостью α.

Натуральная величина образующих находится вращением вокруг горизонтально проецирующей оси, совпадающей с осью конуса.

Концы отрезков соединяем плавной кривой. Развертка боковой поверхности конуса построена.

Развертку боковой поверхности прямого кругового цилиндразаменяют разверткой боковой поверхности правильной многоугольной призмы, вписанной в данный цилиндр.

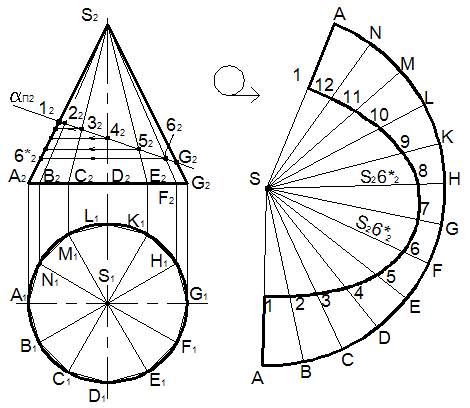
Построим развертку боковой поверхности прямого кругового цилиндра, усеченного плоскостью α.

Делим основание цилиндра на 12 равных частей и проводим через точки деления образующие цилиндра.

На свободном поле чертежа проводим прямую, на которой откладываем последовательно от произвольной точки A равные отрезки A−B, B−C, ... Проводим через точки A, B, C, ... перпендикуляры к прямой и на них откладываем длины соответствующих образующих цилиндра.

Соединив концы образующих, расположенных на участке E−K прямой линией, а на остальных участках – плавной кривой, получаем развертку боковой поверхности усеченного цилиндра.

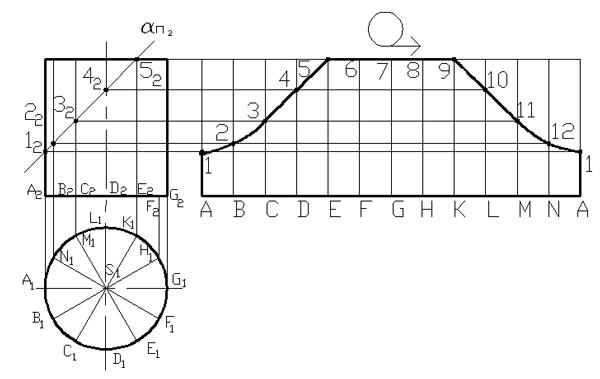
Рассмотрим построение развертки боковой поверхности конуса.

Применяя способ концентрических сфер, строим проекцию линии пересечения заданных конических поверхностей. Сфера минимального радиуса вписывается в больший конус.

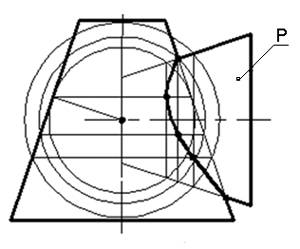
Чтобы построить развертку конуса с линией пересечения заданных поверхностей, вынесем на свободное поле чертежа две проекции конуса, развертку которого мы хотим получить.

Разделим окружность основания конуса на 12 равных частей. Проведем образующие конуса, проходящие через точки деления.

Развертка конуса – это сектор окружности радиусом, равным длине образующей конуса. На дуге окружности, проведенной из произвольной точки S, откладываем участки 1−2, 2−3, 3−4 и т.д., длины которых равны длине соответствующих хорд 1323, 2333 и т.д. окружности основания конуса. Через точки 1, 2, 3, 4 ... проводим образующие конуса, на которых откладываем длины образующих конуса.

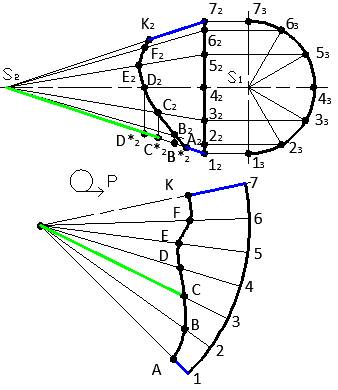
Натуральную величину образующей A конуса определяем по фронтальной проекции конуса – отрезок A212.

Натуральную величину образующей C конуса находим, используя способ вращения вокруг оси, перпендикулярной профильной плоскости проекций Π3 и проходящей через вершину конуса S.

Натуральная величина образующей – отрезок S2C∗. Откладываем эту величину на развертке на образующей C конуса. Натуральные величины остальных образующих находим аналогично