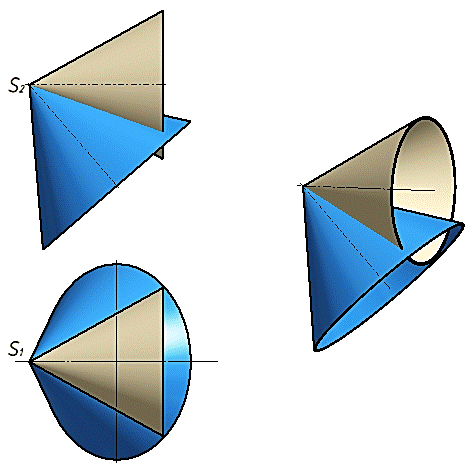
Способ вспомогательных концентрических сфер
Способ применяется при пересечении поверхностей вращения, если их оси в пространстве пересекаются.
Концентрические сферы проводятся из точки пересечения осей поверхностей.
Способ основан на следующих положениях.
Две поверхности вращения с общей осью пересекаются по окружностям, количество которых равно числу точек пересечения главных меридианов поверхностей.
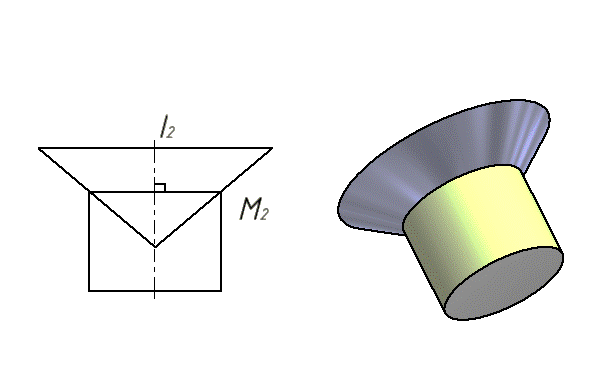
Если центр сферы расположен на оси поверхности вращения, то сфера пересекает данную поверхность по окружностям, которые проецируются на плоскость, параллельную оси, в прямые, перпендикулярные оси поверхности вращения.
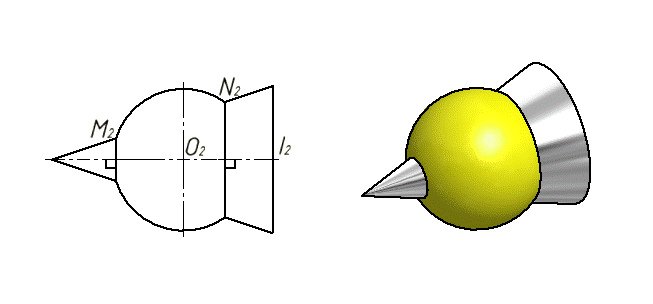
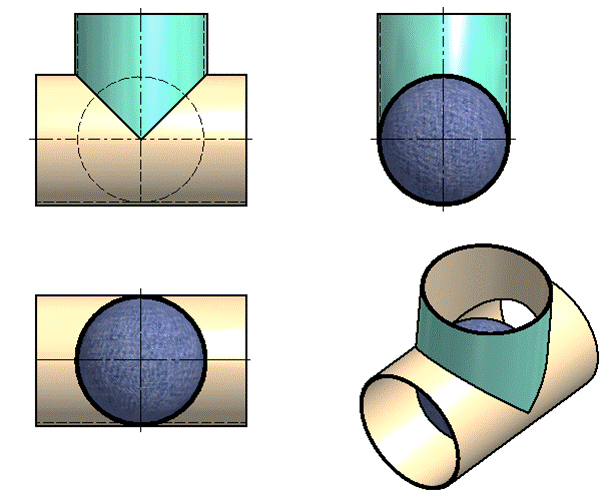
Рассмотрим пересечение цилиндров с пересекающимися осями
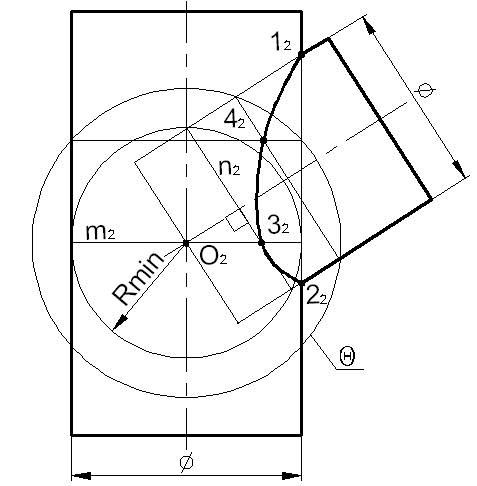

Высшая и низшая точки 1 и 2 линии пересечения определены как точки пересечения очерков обоих цилиндров, поскольку плоскость, проведенная через оси цилиндров, является фронтальной плоскостью уровня.
Точки 3 и 4 получены с помощью двух вспомогательных концентрических сфер. Центр сфер находится в точке O пересечения осей цилиндров. Точка 3 получена с помощью сферы минимального радиуса Rmin. Она касается горизонтального цилиндра по окружности m и пересекает наклонный цилиндр по окружности n. В пересечении фронтальных проекций m2 и n2окружностей получена точка 32. Точка 4 получена аналогично с помощью сферы Θ большего радиуса.
Частные случаи пересечения поверхностей второго порядка
Теорема Г. Монжа
Если две поверхности второго порядка описаны около третьей или вписаны в неё, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания.
Два цилиндра, горизонтально проецирующий и фронтально проецирующий, описаны около одной сферы.
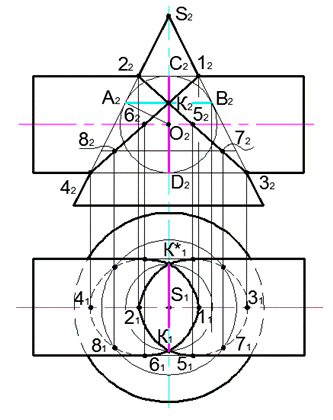
Построим проекции линии пересечения конуса и цилиндра, описанных около одной сферы.
Центр сферы, вписанной в конус и цилиндр, находится в точке О пересечения их осей.
Конус касается сферы по окружности, фронтальной проекцией которой является отрезок (A2 − B2).
Цилиндр касается сферы по окружности, которая на Π2 проецируется в отрезок (C2 − D2).
В пересечении (A2 − B2) и (C2 − D2) получена точка K2. В точку K2 проецируется линия K − K∗, которая соединяет точки касания заданных поверхностей.
Линия пересечения поверхностей распадается на два эллипса, которые на фронтальную плоскость проекций проецируются в прямые, проходящие через точки пересечения очерков конуса и цилиндра –(22 – K2 – 32) и (42 – K2 – 12).
Горизонтальная проекция линий пересечения конуса и цилиндра построена из условия принадлежности линий поверхностям. Точки 5, и 61 принадлежат очерковым образующим конуса и цилиндра и определяют границу видимости на Π1.
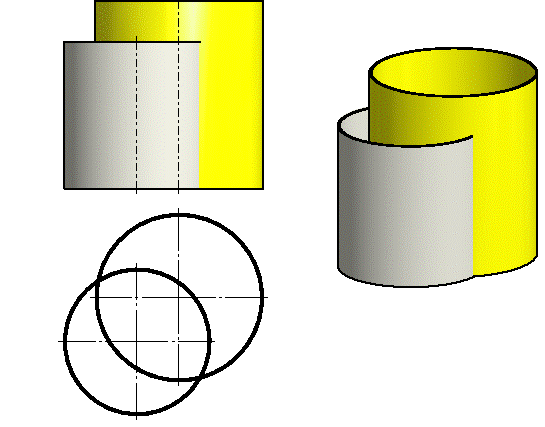
Цилиндры с параллельными осями пересекаются по образующим
Конусы с общей вершиной пересекаются по образующим.