Замена фронтальной плоскости проекций

Расстояние от точки A до плоскости Π1 при замене не меняется:

ZA=const, A1=const. Проекция A4 точки A на плоскость Π4находится на линии проекционной связи, перпендикулярной дополнительной оси X14, на расстоянии ZA от нее, равном расстоянию от точки A до плоскости проекций Π1. ZA определяется из основного чертежа как расстояние от проекции A2 до оси X12.

Замена горизонтальной плоскости проекций

Расстояние от точки B до неизменной плоскости проекций Π2 не изменяется: YB=const, B2=const.

Проекция B5 точки B на плоскость Π5 находится на линии проекционной связи, перпендикулярной новой оси координат X25, на расстоянии YA от нее.

Замена одной из плоскостей проекций не всегда приводит к решению задачи. Иногда приходится заменять две и более плоскостей проекций.

Рассмотрим перевод прямой AB общего положения в проецирующее положение

Выполняется последовательная замена двух плоскостей проекций.

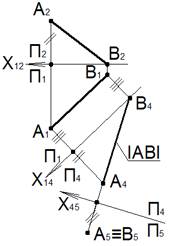
Первая замена

Новая системе плоскостей Π1⊥Π4.

Π4∥AB⇒A4B4=|AB|

На комплексном чертеже ось координат X14∥A1B1.

Линии проекционной связи проводятся перпендикулярно оси X14. При замене плоскости Π2 на плоскость Π4 расстояние всех точек прямой AB до плоскости Π1 (координата Z) не изменилось, поэтому расстояние проекций точек A4 и B4 от оси X14 равно расстоянию проекций точек A2 и B2 от оси X14.

В заданной системе плоскостей одновременно можно заменять только одну плоскость.

Вторая замена

Новая системе плоскостей Π4⊥Π5.

Π5⊥AB⇒A5≡B5

Линии проекционной связи проводятся перпендикулярно оси X45. При замене плоскости Π1 на плоскость Π5 расстояние всех точек прямой AB до плоскости Π4 не изменилось, поэтому расстояние проекций точек A5 и B5 от оси X45 равно расстоянию проекций точек A1 и B1 от оси X45.

Рассмотрим перевод плоскости α общего положения во фронтально проецирующее положение

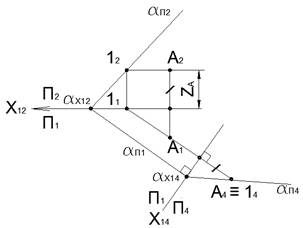
Новая система плоскостей Π1⊥Π4

Π4⊥α⇒X14⊥αΠ1∧X14⊥(11−A4)

Линия проекционной связи A1−A4 проводится перпендикулярно оси X14. При замене плоскостиΠ2 на плоскость Π4 расстояние точки, принадлежащей плоскости α, A∈α, до плоскости Π1(ZA)не изменилось, поэтому расстояние проекций точек A4 и 14 от оси X14 равно расстоянию проекций точек A2 и 12 от оси X12.

Пример

Найти натуральную величину треугольника ABC и угол наклона его плоскости к горизонтальной плоскости проекций Π1.

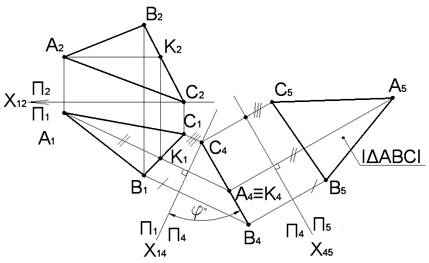
Выберем новую плоскость проекций Π4, перпендикулярную плоскости треугольника ABC, а на комплексном чертеже – перпендикулярную горизонтали AK плоскости треугольника:

Π4⊥△ABC, Π4⊥AK, AK∈△ABC, AK∥Π1

Проводим новую ось координат X14 перпендикулярно A1K1:X14⊥A1K1

Имеем систему взаимно перпендикулярных плоскостей Π1⊥Π4. Плоскость △ABC по отношению к плоскости Π4 будет проецирующей. Проводим линии проекционной связи от точек A1,B1,C1 и откладываем координаты Z вершин треугольника от новой оси X14, получаем проекции точек A4,B4,C4. Проекция треугольника ABC на Π4 – прямая C4B4, составляющая с осью X14 угол, равный натуральной величине угла между плоскостью треугольника и Π1 – угол φ.

Чтобы найти натуральную величину треугольника заменяем плоскость Π1. Вводим новую плоскость Π5, параллельную плоскости треугольника. Параллельно вырожденной проекции треугольника C4B4 проводим новую ось X45. На линиях проекционной связи отложим от новой оси отрезки, равные расстояниям от заменяемых проекций вершин A1B1C1 до заменяемой оси X14. A5B5C5=|△ABC|.