Принадлежность точки и линии плоскости. Главные (особые) линии плоскости

Точка в плоскости выбирается из условия, что она находится на прямой линии этой плоскости.

Прямая линия принадлежит плоскости при условии, если она проходит:

· через две точки плоскости;

· через точку плоскости параллельно любой прямой этой плоскости.

На рисунке плоскость α задана пересекающимися прямыми AB и BC: α(AB∩BC).

Точки A и K расположены на прямых, которыми задается плоскость α:

A∈AB∈α⇒A∈α, K∈BC∈α⇒K∈α

Прямая AK принадлежит плоскости α: AK∈α. Через точку C можно провести прямую CD, параллельную AB. Эта прямая по условию принадлежит плоскости α(AB∩BC).

CD∥AB∈α∧C∈α⇒CD∈α

К главным линиям плоскостиотносят линии уровня плоскости, параллельные плоскостям проекций, и линии наибольшего наклона плоскости к плоскостям проекций.

Горизонталь плоскости – прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций Π1.

Фронтальная проекция горизонтали параллельна оси OX. Фронтальный след горизонтали принадлежит фронтальному следу плоскости α.Горизонтальный след плоскости αΠ1 называетсянулевой горизонталью (Z−0).

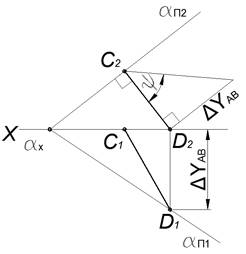
На рисунке показана горизонталь плоскости α⊥Π1.

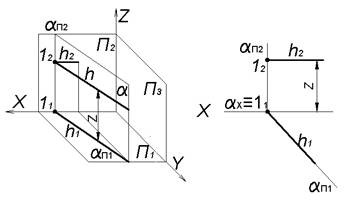
Фронталь плоскости – прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций Π2.

Линия наибольшего наклона плоскости к горизонтальной плоскости проекций Π1(линия ската) – прямая, принадлежащая плоскости и перпендикулярная горизонтали плоскости.

Линия наибольшего наклона плоскости к фронтальной плоскости проекций Π2 – прямая, принадлежащая плоскости и перпендикулярная фронтали плоскости.

В плоскости α общего положения проведены произвольные горизонталь – AB и линия ската – DE:

AB∈α∧AB∥Π1

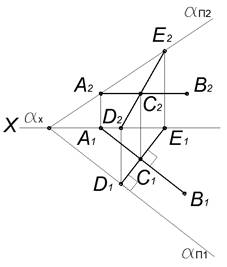
Фронтальная проекция A2B2 горизонтали AB параллельна оси OX, горизонтальная проекция A1B1 параллельна горизонтальную следу плоскости αΠ1. Прямой угол, который линия ската составляет с горизонталью плоскости, проецируется на горизонтальную плоскость проекций Π1без искажения. Фронтальная проекция линии ската D2E2 определяется по условию принадлежности плоскости α:

D1E1⊥A1B1∧D1E1⊥αΠ1, D2∈OX∧E2∈αΠ2.

В плоскости общего положения проведены произвольно фронталь AB и линия наибольшего наклона плоскости α к Π2 – DE.

AB∈α∧AB∥Π2, DE∈α∧DE⊥AB.

Горизонтальная проекция A1B1 фронтали AB параллельна оси координат OX, фронтальная проекция A2B2 параллельна фронтальному следу плоскости αΠ2:

Прямой угол между фронталью и линией наибольшего наклона плоскости α к Π2 проецируется без искажения на фронтальную плоскость проекций Π2. Горизонтальная проекция линии наибольшего наклона D1E1 строится как недостающая проекция из условия принадлежности плоскости

α:D2E2⊥A2B2∧D2E2⊥αΠ2,D1∈αΠ1∧E1∈OX

Главным свойством линии ската является то, что она образует с горизонтальной плоскостью проекций Π1 угол φ, равный углу наклона плоскости α к плоскости проекций Π1. На рисунке использован способ прямоугольного треугольника для определения φ=(1−2)∧Π1=α∧Π1.

Линия наибольшего наклона плоскости α к Π2 наклонена к плоскости проекций Π2 под углом ψ, равным углу наклона плоскости α к плоскости проекций Π2. На рисунке использован способ прямоугольного треугольника для определения ψ=(3−4)∧Π2=α∧Π2.