Взаимное положение геометрических фигур на плоскости

Наблюдения, специальные исследования, опыт работы показы­вают, что умственно отсталые школьники испытывают значительные трудности в установлении взаимоотношения предметов в пространст­ве и на плоскости. Пространственные представления у учащихся развиты слабо. Неполноценность межанализаторных связей, запаз­дывание формирования речи и двигательной активности — это те неблагоприятные условия, в которых формируются представления о пространственных признаках и отношениях окружающих предметов.

Наблюдения на уроках математики показывают, что учащиеся вспомогательной школы, особенно младших классов, испытывают большие затруднения в оценке отношений объектов между собой. Например, стул стоит перед, сзади, слева, справа, около,застолом; точка расположена ниже, выше, наотрезке. Без специального обучения даже учащиеся старших классов вспомогательной школы не понимают, что одна фигура может касаться, пересекаться, принад­лежать или не принадлежать другой. В связи с этим уже на пер­вых годах обучения следует развивать у детей пространственную ориентировку.

В пропедевтический период необходимо учить детей определять положение предметов относительно себя и друг друга. Достигается это путем выполнения школьниками определенных практических действий как на уроках, так и во внеурочное время. Выполнение действий сопровождается объяснением; учитель дает образец выпол­нения практического действия и его комментарий. Начинать следует с живых объектов. Например: «Я стою около Вити. Дети, где я стою? Наташа, встань рядом со мной. Рядом с кем стоит Наташа? Катя встанет между Колей и Сашей. Между кем из ребят стоит Катя? Ва­ня встанет перед (за) Олей. Где встал Ваня? Саша сделал шаг влево (вправо, вперед, назад)...» Учащиеся постепенно овладевают значением предлогов и наречий, указывающих на пространственные отношения предметов. Положительного результата можно добиться путем практических действий, выполняемых самими учениками, про­ведением дидактических и подвижных игр, направленных на разви­тие их пространственных представлений.

Существует зависимость понимания пространственных отношений предметов, а также умения ориентироваться в пространстве от степени владения предлогами и наречиями, обозначающими эти отношения. После того как ученики научатся по заданию учителя ориентироваться в пространстве и определять положение предме­тов относительно себя, следует переходить к формированию понятий о пространственных отношениях между предметами. С этой целью учитель выполняет действие спредметами и сопровождает это действие проговариванием (комментирует). Ученики воспроизводят это действие и тоже сопровождают его речью. Например: «Тетрадь я положу рядом (около, слева, справа и т. д.) с книгой», «Карандаш лежит на тетради».

Далее следует рассматривать взаимное положение геометриче­ских фигур относительно друг друга.

В I, II классах дети знакомятся со следующими геометриче­скими фигурами: точкой, прямой и кривой линиями, отрезком, кру­гом, квадратом, треугольником, прямоугольником.

На этом этапе обучения целесообразно обратить внимание уча­щихся и на взаимное положение фигур относительно друг друга на таблице, наборном полотне, доске, учительском и ученическом столах. Например, точка вышепрямой, круг лежит слеваот тре­угольника, квадрат находится междуотрезком и кругом, треуголь­ник находится внутриквадрата и т. д. Наряду с определением положения фигур относительно друг друга учащиеся должны вы­полнять и практические действия, которые закрепляли бы представ­ления о взаимном положении фигур. Например: «Положи круг слеваот треугольника, квадрат вышекруга, надкругом и т. д.», «На серединулиста бумаги положи круг и обведи его», «Положи рядомдва синих квадрата, междуними положи красный прямоуголь­ник».

Работа выполняется на ученическом столе с моделями фигур, которые дети располагают определенным образом по заданию учи­теля. Упражнения могут носить и занимательный характер. На наборном полотне располагаются геометрические фигуры — в сере­дине круг, а слева и справа от него квадрат и треугольник. Учитель просит внимательно посмотреть и запомнить, как располо­жены фигуры. Затем он говорит: «Подул ветер и все фигуры перемешал. Кто лучше запомнил, как лежали фигуры? Положите их на своем столе в том же порядке и расскажите, как они расположены». Такого типа упражнения полезны тем, что тренируют и развивают память.

Во II классе школьники вычерчивают произвольно треугольники, четырехугольники по точкам. Им могут быть предложены задания ни пересечение прямыми треугольников, четырехугольников, кругов. Например: «Начертите треугольник (круг, квадрат), начертите пря­мую линию так, чтобы она пересекала треугольник (круг, квадрат)».

В III классе рассматривается пересечение прямых (кривых) ли­ний, отрезков. Дети выделяют точку пересечения. Если раньше учащиеся знали, что через одну точку можно провести много прямых, к) в III классе об этих же прямых они скажут, что много прямых

пересекается в одной точке. При пересечении прямой, круга, вы­пуклого многоугольника (IV класс) можно говорить о двух точках пересечения. Если прямая не пересекает круг, многоугольник и не касается их, то она находится (лежит) вне этих фигур.

В V классе учитель знакомит детей с понятием принадлежит (не принадлежит).Точка принадлежит прямой, лучу, отрезку, окруж­ности, кругу, многоугольнику. Понятия принадлежити находится внесопоставляются.

В V классе появляется возможность пополнить знания детей новыми сведениями о положении фигур относительно друг друга и ввести понятие касается.Прямая, луч, отрезок, окружность, круг, многоугольник могут касаться, т. е. иметь одну общую точку.

В V классе дети знакомятся со случаями: 1) касания геомет­рических фигур; 2) пересечения кругов, многоугольников; 3) одна фи­гура принадлежит другой, т. е. одна фигура целиком помещается в другой.

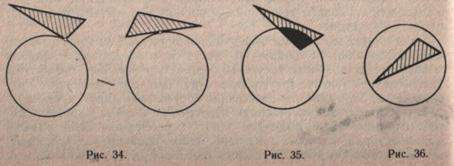
Дети работают с моделями фигур. Учитель дает задание поло­жить две фигуры на плоскости так, чтобы они касались друг друга, т. е. имели общую точку. Например, учащиеся имеют модель круга и треугольника. Они прикладывают их друг к другу так, как показано на рисунке 34.

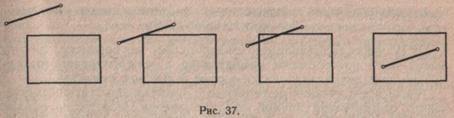
Затем учитель располагает фигуры так, чтобы они пересекались (рис. 35). Учащиеся говорят, что фигуры пересекаются, и объясня­ют, почему они так считают (часть одной фигуры принадлежит другой).

Наконец, учитель показывает, что одна фигура может полностью принадлежать другой, тогда говорят: «Одна фигура находится внутри другой» (рис. 36). В данном случае треугольник принадле­жит кругу или находится внутри его.

Учащиеся работают с моделями фигур. Они прикладывают их друг к другу (фигуры касаются), накладывают друг на друга (фигуры пересекаются или одна фигура принадлежит другой).

Наряду с многоугольниками учащиеся используют и модели угла.

Только после работы с моделями фигур можно переходить к рассмотрению и определению положения фигур относительно друг друга на чертежах.

В дальнейшем при повторении геометрического материала, изу-

ченного в I—V классах, обобщаются все случаи взаимного поло­жения фигур. С этой целью ученикам предъявляются чертежи с геометрическими фигурами, изображенными в разном взаимном по­ложении. Ученики должны рассказать, как расположены фигуры от­носительно друг друга.

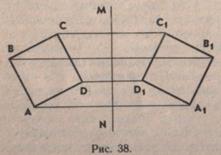
Целесообразно показать чертеж, на котором изображены две геометрические фигуры, касающиеся друг друга. Учитель просит представить себе и рассказать, как еще могут быть расположены эти фигуры относительно друг друга. Или учитель называет две фигуры, а ученики вычерчивают их в различном положении отно­сительно друг друга. Например, даны точка и луч. Ученики вы­черчивают точку вне луча, точку, принадлежащую лучу. Или даны отрезок и прямоугольник. Учитель ставит задачу начертить (рис. 37) отрезок вне прямоугольника; отрезок, пересекающий прямоуголь­ник; отрезок, имеющий с прямоугольником одну общую точку (ка­сается); отрезок, находящийся внутри прямоугольника (принадле­жит).

Учащиеся рассказывают о взаимном положении отрезка и прямо­угольника на каждом чертеже, комментируют свои построения.

Можно предложить школьникам выполнить аналогичные чертежи с кругом и треугольником, а затем рассказать о взаимном положении этих фигур.

Учащиеся знакомятся с пересекающимися прямыми и отрезками. Среди пересекающихся прямых с помощью угольника они находят такие, которые при пересечении образуют четыре прямых угла (взаимно перпендикулярные).Они учатся отыскивать взаимно пер­пендикулярные прямые на чертежах, геометрических фигурах, окру­жающих предметах (крышка стола, классная доска, оконная рама и т. д.), вычерчивать их.

Учащиеся также узнают, что прямые могут быть расположены так, что, сколько бы их ни продолжали, они не имеют общих точек, т. е. прямые параллельные.Расстояние между параллельными равно длине перпендикуляра, опущенного или восстановленного из точки на одной прямой к другой. Причем ученики должны убедиться, что расстояние между двумя данными параллельными прямыми всегда одно и то же. Если оно увеличивается или уменьшается,

то прямые не параллельны, а пересекаются.

Нельзя ограничиваться рассмотрением параллельности только двух прямых. Их может быть и три, и более, расстояние между отдельными парами может быть различным.

6. СИММЕТРИЧНЫЕ И СИММЕТРИЧНО РАСПОЛОЖЕННЫЕ ФИГУРЫ. ОСЬ, ЦЕНТР СИММЕТРИИ

В IV же классе учащиеся узнают о том, что предметы, фигуры могут быть расположены симметричнои несимметричноотноси­тельно друг друга, знакомятся с осьюи центром симметрии.

Чаще всего ученики встречаются с симметричностью предметов, фигур относительно прямой при выполнении заданий на уроках рисования, труда. Копируя действия учителя, они располагают фигу­ры, их элементы симметрично, но не всегда называют признаки симметричных фигур. В повседневной жизни дети нередко слышат о симметрично расположенных домах, окнах в комнате, пуговицах на одежде, картинах на стенах, предметах на рисунке и т. д.

Учитель сначала знакомит школьников с симметричными предме­тами. Он показывает, например, рисунок пирамидки (игрушки), пе­регибает его так, чтобы совпали правая и левая части. Расправив рисунок, учитель показывает линию сгиба, проводит по этой линии прямую — ось рисунка, просит сравнить правую и левую части пирамидки. Учащиеся делают вывод, что они одинаковые.

Учитель говорит детям, что такой предмет называется симмет­ричным. Его можно разделить на две одинаковые части. Прямая, ко­торая делит рисунок на две одинаковые части или на две половин­ки, называется осью симметрии.

Рассматриваются рисунки яблока, груши, арбуза и др. на проз­рачной бумаге. Путем перегибания рисунка по оси симметрии уста­навливается, что предметы, изображенные на рисунке, симметричны.

Затем учитель предлагает школьникам взять рисунки различных предметов (на прозрачной бумаге) и отобрать из них такие, на которых изображены симметричные предметы. Ученики должны доказать правильность выбора рисунка.

От изображений симметричных и несимметричных предметов следует перейти к рассмотрению самих предметов, например листа дерева, форменного фартука, рубашки мальчика, пионерского галсту­ка. Все перечисленные предметы легко сложить так, чтобы убедиться, что их половины совпадают, т. е. равны, следовательно, эти предметы симметричны.

Затем рассматриваются геометрические фигуры. Учащиеся должны определить, какие из известных им фигур симметричны, найти оси симметрии. Например, берут круг, перегибают его по диаметру, половины круга совпали. Следовательно, круг — фигура симметричная, ось симметрии круга — диаметр.

Но в круге можно построить не один диаметр, а много. Школь­ники должны убедиться в том, что круг имеет бесконечное коли­чество осей симметрии.

Учащиеся получают равносторонний треугольник. Перед ними снова ставится задача установить, является ли данная фигура сим­метричной. Перегибая модель треугольника, учащиеся убеждают­ся, что равносторонний треугольник — симметричная фигура, а осью симметрии является прямая, проходящая через вершину треуголь-

ника и середину противоположной стороны. Учитель предлагает учащимся перегнуть треугольник по прямой, проходящей через дру­гую вершину и середину противоположной ей стороны треугольника, и т. д. Дети делают вывод, что в равностороннем треугольнике можно провести три оси симметрии.

Аналогичные действия школьники проделывают с равнобедрен­ными и равносторонними треугольниками, они убеждаются, что равнобедренный треугольник имеет всего одну ось симметрии, про­ходящую через его вершину и середину основания, а разносторон­ний треугольник не имеет осей симметрии, т. е. разносторонний треугольник — фигура несимметричная.

Наконец, предлагается установить, являются ли симметричными известные учащимся четырехугольники (прямоугольник, квадрат, параллелограмм, ромб), и определить их оси симметрии. В этом случае учащиеся должны проявить максимум самостоятельности, использовать свой опыт, знания и сделать соответствующие выводы. Перегибанием прямоугольника учащиеся находят две его оси симметрии и приходят к выводу, что прямоугольник — симметричная фигура.

Так же, чисто практически, школьники устанавливают, что па­раллелограмм — несимметричная фигура, а ромб — симметричная фигура, всякий другой параллелограмм (не являющийся ни прямо­угольником, ни ромбом) не имеет ни одной оси симметрии.

Особо интересная фигура — квадрат. Поскольку он является и прямоугольником и ромбом, то имеет такие же оси симметрии, как любой прямоугольник (оси симметрии проходят через середины противоположных сторон), и такие же, как любой ромб (оси сим­метрии проходят через противоположные вершины).

На уроке, обобщающем знания детей о симметричных и не­симметричных фигурах, следует предложить учащимся модели, чер-тежи геометрических фигур для того, чтобы они отыскивали оси симметрии, устанавливали, какие фигуры являются симметричными (относительно прямой), какие нет. Учитель может поставить задачу развить пространственное воображение учащихся, задавая им такие вопросы: «Не перегибая фигур, ответьте на вопросы: является ли диагональ осью симметрии прямоугольника, квадрата, параллело­грамма, ромба? Если провести прямую через середины противо­положных сторон ромба, будет ли она являться осью симметрии? Сколько осей симметрии в квадрате? Какая из четырех фигур: ромб, прямоугольник, параллелограмм, квадрат — несимметрич­ная?»

На обобщающем уроке следует предложить учащимся модели, чертежи геометрических фигур с целью нахождения среди них симметричных и определения в них осей симметрии.

После изучения симметричных фигур следует рассматривать сим­метрично расположенные предметы и фигуры. Например, на рисун­ке — ель, ствол которой изображен в виде отрезка прямой, а по обе стороны на равном расстоянии от нее два одинаковых дома. Если перегнуть рисунок ствола дерева, то изображения домов совпадут.

Про эти дома можно сказать, что они симметрично расположены относительно ствола дерева. Учитель помещает на доску рисунок и просит учащихся два других рисунка поместить симметрично первому; ставит стул и просит два других поставить симметрично первому и т. д.

Затем учитель предлагает детям провести на листе бумаги пря­мую, перегнуть лист по этой линии, на некотором расстоянии от линии сгиба проткнуть бумагу булавкой. Полученные точки (следы прокола) симметричны относительно прямой — оси симметрии.

Учащимся дается задание вычертить одинаковым радиусом с центрами в точках прокола круги на правой и левой половинах листа бумаги. Согнуть лист так, чтобы круги совместились. Линия сгиба — это ось симметрии, сообщает учитель, а круги симметричны относительно этой оси.

Учитель знакомит школьников со способом получения многоуголь­ника, симметричного данному. На листе бумаги изображается много­угольник и ось симметрии. Лист сгибается по оси. Булавкой прокалы­ваются вершины многоугольника. Затем точки, полученные на про­тивоположной половине листа, соединяются. Таким образом получил­ся многоугольник, симметричный данному.

Школьникам могут быть предложены чертежи одинаковых геомет­рических фигур, а также парные рисунки одинаковых предметов. Дети должны совместить фигуры или рисунки предметов и получить ось симметрии. Если фигуры (рисунки) совмещаются, значит, они симметрично расположены относительно оси.

Симметрично и несимметрично расположенные предметы отыски­ваются в окружающей обстановке (в классе, столовой, физкуль­турном зале, учебной мастерской). Такие задания выполняются на глаз.

В IV классе учащиеся знакомятся с новым понятием — центром симметрии и рассматривают предметы, фигуры, симметричные от­носительно центра симметрии.

На прямой выделяется цветом точка О — центр симметрии. На одинаковом расстоянии, по обе стороны от точки О, на прямой отмечаются точки А и В. Учитель указывает на то, что точки А, В, О принадлежат одной прямой. Измеряются отрезки АО и ОВ. Ученики убеждаются, что АО = ОВ, делается вывод, что точки А и В симметричны относительно центра симметрии О.

На доске (или таблице) изображены еще две точки — С и D, они не соединены отрезком. Учитель просит учащихся сказать, являются ли точки С и D симметричными относительно центра симметрии О. Мнения учащихся расходятся. Учитель объясняет: «Для того чтобы ответить на поставленный вопрос, нужно соединить точки С и D отрезком. Пусть отрезок CD проходит через точку О. Далее надо измерить расстояние от точки О до точек С и D. Если отрезки СО и CD имеют одинаковую длину, то точки С и D сим­метричны относительно центра симметрии О».

Предлагается еще пара точек М и К. Школьники должны определить, являются ли точки симметричными относительно точки О.

Учащиеся уже знают, что точки М и К надо соединить отрезком, оказывается, что отрезок МК не проходит через точку О. Учитель помогает школьникам сделать вывод, что точки М и К несимметричны относительно точки О.

Новая пара точек — Е и S — соединяется отрезком. Отрезок ES проходит через точку О, но, измеряя отрезки ЕО и OS, дети устанавливают, что они не равны, следует вывод, что точки Е и S несимметричны относительно точки О.

После этого учитель может предложить каждому ученику карточ­ку, на которой изображена.точка О, а вокруг неё несколько пар точек. Каждая пара точек, которую будут исследовать школьники, изображается одним цветом (две красные точки, две зеленые, две синие и т. д.). Учащиеся определяют, точки какой пары являются симметричными относительно точки О — центра симметрии.

Некоторые учащиеся вспомогательной школы с большим трудом запоминают геометрические термины, выражения, у них медленно формируются представления о возможных взаимных положениях фигур, предметов (фигуры касаются, пересекаются, принадлежат одна другой, находятся вне друг друга) и относительно оси и центра симметрии (симметричные, несимметричные). Поэтому необ­ходимо изготовить таблицу, на которой изображены различные варианты расположения геометрических фигур относительно друг друга, относительно оси и центра симметрии, с соответствующими краткими текстами.

Когда большинство учащихся свободно ориентируется в понятиях расположения фигур, не нуждается в таблице, она убирается. Для отдельных школьников по мере необходимости изготавливается копия такой таблицы для индивидуального пользования.

В VII классе в соответствии с требованиями программы знания детей о симметричных фигурах расширяются.

При повторении знаний о фигурах, симметричных относительно оси, для изображений следует использовать плоскость, которую нельзя перегнуть: вычерчиваются фигуры (точки, отрезки, круги, многоугольники) на классной доске, на листе фанеры. Учитель ставит перед детьми задачу: определить, являются ли, например, точки А и В, изображенные на доске, симметричными относительно оси. Учитель выслушивает ответы учащихся и подводит их к выводу: чтобы определить, являются ли точки А и В симметричными относительно оси, надо: 1) соединить их отрезком, который пересечет ось симметрии в точке О; 2) проверить с помощью угольника, является ли отрезок АВ перпендикуляром к оси симметрии; 3) из­мерить расстояние от точек Л и Б до точки О, т. е. установить, равны ли отрезки АО и ОВ. Если все эти условия выполнены, то точки А и В являются симметричными относительно оси сим­метрии. Значит, симметричными относительно оси симметрии являются такие точки, расстояние (по перпендикуляру) от которых до оси симметрии одинаковое.

Дети должны усвоить порядок действий, который необходимо

выполнять, чтобы установить, являются ли точки симметричными.

Для этого нужно рассмотреть случаи: 1) точки принадлежат одному отрезку, но отрезок, соединяющий их, не перпендикулярен оси; 2) точки находятся на перпендикуляре к оси симметрии, но на разном от нее расстоянии.

Учащимся предлагаются разные виды упражнений, в которых требуется установить, являются ли пары точек симметричными относительно оси.

Например, исследуется пара точек, изображенных одним цветом, и ось симметрии. Требуется установить, являются ли они симметрич­ными относительно данной оси симметрии. Для того чтобы ответить на вопрос, дети соединяют точки, отмечают точку пересечения полученного отрезка с осью симметрии. Проверяют, является ли отрезок перпендикуляром к оси, на одинаковом^- ли расстоянии находятся точки от оси симметрии. После этого школьники делают вывод, являются ли данные точки симметричными относительно оси симметрии.

Симметричными относительно прямой могут быть и другие гео­метрические фигуры. Так, два отрезка симметричны, если их концы являются симметричными отрезками.

Учитель показывает треугольники, квадраты, прямоугольники и т.д., симметричные относительно оси. Дети устанавливают сим­метричность относительно оси их вершин, тождественность сим­метричных фигур (равенство сторон, углов).

Круги одного радиуса будут симметричными только в том случае, если симметричны их центры.

В VII, VIII классах учитель знакомит учеников с построением фигур, симметричных относительно точки. Начать следует с построе­ния точки, симметричной данной относительно центра симметрии. Даны центр симметрии О и точка А. Нужно построить прямую, проходящую через точки Л и О, и измерить отрезок О А. На этой прямой отложить отрезок ОВ, равный ОА. Конец отрезка ОВ — точка В — симметричен точке А.

Затем учащиеся знакомятся с построением точки (отрезка, много­угольника, круга), симметричной относительно оси симметрии данной точке (отрезку, многоугольнику, кругу).

Например, дана точка А. Нужно построить точку В, ей симмет-

ричную относительно оси симметрии CD. Построение: 1) из точки А восставить перпендикуляр к оси симметрии CD и продолжить его; 2) обозначить точку пересечения перпендикуляра с осью симметрии буквой О; 3) измерить расстояние ОА; 4) от точки О отложить циркулем отрезок ОВ, равный ОА. Точка В симметрична точке А.

Для построения окружности, симметричной данной, необходимо построить точку, симметричную ее центру, а затем вычертить новую окружность того же радиуса.

Если дан отрезок АВ и необходимо построить отрезок, симмет­ричный ему, строятся точки А₁ и В₁ симметричные точкам А и В; соединив точки А₁ и В₁, получим искомый отрезок А₁В₁.

Для построения квадрата A₁B₁C₁D₁, симметричного данному квадрату ABCD относительно оси симметрии MN, нужно построить 4 точки (вершины), симметричные вершинам данного квадрата относительно оси симметрии (рис. 38).

В дальнейшем полезно выполнять задания, в которых требуется установить, являются ли геометрические фигуры симметричными относительно прямой — оси симметрии.

С построением геометрической фигуры (точки, отрезка, много­угольника, круга), симметричной относительно точки, следует по­знакомить учащихся VIII класса.

Например, нужно построить точку А_1, симметричную точке А относительно центра симметрии — точки О. Для этого нужно через точку О — центр симметрии и точку А провести прямую. Измерив циркулем расстояние от точки О до точки А, отложить его на прямой по другую сторону от точки О. Получим точку А₁. А и А₁ — симметричные точки относительно центра симметрии О.

Если две точки А и В, симметричные относительно точки О, принять за центры окружностей и построить две окружности с одинаковыми радиусами, то получим две симметричные окружности относительно центра симметрии О.

В этом можно убедиться, если через центр симметрии построить перпендикуляр к прямой АВ. Этот перпендикуляр является осью симметрии точек А и В и окружностей с центрами в точках А и В.

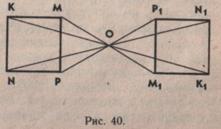
Квадрат K₁M₁P₁N₁ симметричен квадрату KMPN относительно центра симметрии О.

Таким образом, изучение вопросов взаимного положения геометрических фигур на плоскости продолжается в течение всех лет обучения школьников математике, уточнение и рас­ширение знаний учащихся про­исходит постепенно от класса к классу.

Знания, полученные при изуче­нии данных вопросов, будут способствовать формированию пространственных и геометрических

представлений, развитию воображения учащихся вспомогатель­ной школы и позволят им быстрее адаптироваться в окружающей среде.

ГЕОМЕТРИЧЕСКИЕ ТЕЛА

В I и II классах учащиеся знакомятся с шаром, кубом, брусом, их внешним видом, названием, рассматривают геометрические тела как целое, не выделяя его элементов. Эти геометрические тела учащиеся различают, они знакомы детям по игровой деятельности, однако названия геометрических тел долгое время не запоминаются детьми и не используются в активном словаре, чаще всего они употребляют бытовые названия этих тел: шарик, кубик, домик, столбик и др.

Знакомство с каждым геометрическим телом, даже если дети уже знают его название, следует проводить постепенно, сопоставляя геометрическое тело со сходной геометрической фигурой.

Например, при знакомстве с шаром учитель приносит в класс модели шаров различных цветов и размеров, изготовленных из разных материалов, предметы, по форме напоминающие шар,— клубок ниток, воздушный шар, апельсин и т. д. Шар сравнивается с уже известной учащимся геометрической фигурой — кругом. Уча­щиеся кладут круг и шар на почти горизонтальную плоскость. Шар катится, круг не катится. Дети берут в ладошки шар, круг. Они лепят шар из пластилина, а круг обводят по шаблону, раскра­шивают, вырезают. Зрительно и на ощупь дети чувствуют различие шара и круга. Чтобы учащиеся дифференцировали названия круга и шара, полезно сделать плакат, на одной половине которого прикреплен (нарисован) круг, а на другой — шар. Под кругом и шаром учащиеся прикалывают соответственно рисунки предметов; напоминающих круг и шар.

Аналогично проходит знакомство детей с кубом, который со­поставляется с квадратом, а во II классе — с брусом (брус со­поставляется с прямоугольником).

Следует обратить внимание учащихся на те предметы, которые имеют форму шара, куба, бруса. Так, демонстрируя некоторые предметы, учитель задает вопрос учащимся: «Какую форму имеют арбуз, мяч, коробка и т. д.?» Или: «Это шар. Посмотрите вокруг и назовите предметы, которые имеют форму шара». В следующих классах следует развивать наблюдательность детей, сопоставляя предметы, имеющие форму куба и бруса, в обстановке вне класса, рассматривая уже не мелкие предметы, которые можно взять в руки, а крупные, такие, как поленницы дров, различные строения и т. п., а также отдельные части предметов, например кузов грузовика и т. д. В V классе учащиеся знакомятся с элементами куба и бруса: грань, ребро, вершина. Грань — непривычное для учащихся слово, они часто называют грань стороной куба, 6pyca. Следует пре­дупредить такого рода ошибку, помогая учащимся многократной

постановкой вопросов: «Покажи грани. Где грани? Пересчитай все грани... Какой геометрической фигурой является каждая грань куба? ... Какой геометрической фигурой является каждая грань бруса?» И т.д.

Чтобы учащиеся могли показать, не пропуская, все грани куба, бруса (не указывая больше одного раза на каждую грань), сле­дует предложить учащимся ту последовательность показа граней, которой они будут всегда придерживаться (и в старших классах). Такой последовательностью может быть перечисление сначала ос­нований (нижнего, верхнего), затем боковых граней. Этот же порядок сохраняется при показе ребер и вершин. Так, первыми показываются ребра нижнего, затем верхнего оснований, наконец, боковые ребра. Далее выделяются вершины нижнего, затем верхнего оснований. Порядок показа элементов геометрических тел может быть и другой, но важно его сохранить одинаковым для всех лет обучения уча­щихся данного класса.

Познакомив учащихся с гранями, ребрами, вершинами бруса и куба, а также их количеством и вооружив их приемами практичес­кой деятельности и организацией этой деятельности при опреде­лении количества элементов этих тел, учитель переходит к объяс­нению свойств граней и ребер.

В младших классах целесообразно использовать индуктивный путь познания. Учитель предлагает учащимся поставить брус (куб) на страницу тетради, принимая за основание то одну, то другую грань, и последовательно обвести каждую грань, просит определить, какие фигуры получились. Учитель дает задание сравнить все грани куба. Последовательно прикладывая грани куба к полученным квад­ратам, учащиеся убеждаются, что все грани куба — квадраты равны между собой. Эта работа носит характер небольшого исследования.

Далее определяется форма граней бруса. Устанавливается фор­ма нижней и верхней граней. Они сравниваются наложением бруса на чертеж. Затем устанавливаются форма и размеры боковых граней бруса. Необходимо показать такие брусы, в основании которых лежат и квадраты.

На основании практических работ, измерений, наблюдений уча­щиеся самостоятельно должны сделать вывод о форме и размерах граней бруса. «Грани бруса — прямоугольники, в том числе квад­раты». Необходимо требовать от учащихся развернутых ответов, умения обосновать правильность вывода путем выполнения практи­ческих работ.

Аналогично изучаются свойства ребер куба и бруса. По одному из ребер изготовляется мерка, с помощью этой мерки измеряются другие ребра, устанавливается, что противоположные ребра равны, равенство ребер увязывается с равенством граней.

Очень трудно для учащихся V класса вспомогательной школы рассматривать ребро как результат пересечения двух граней, а вершину как результат пересечения трех его граней. Поэтому луч­ше обратить внимание учащихся на принадлежность каждого реб­ра двум граням. Они смогут показать ребро и грани, которым это ребро принадлежит. Также им вполне доступно показать одну из вершин и три ребра, которым она принадлежит.

1 13

Учащиеся должны твердо знать, что ребра — это отрезки, вер­шины — точки. На предметах, имеющих форму куба, бруса, дети должны научиться выделять грани, ребра, вершины.

Опыт учащихся в изучении геометрических тел следует рас­ширять за счет сравнения различных кубов и брусов. Кубы отли­чаются друг от друга размерами, однако количество элементов в каждом кубе остается постоянным. Свойства граней, ребер куба также неизменны — все это существенные признаки куба. Размеры, материал, из которого он сделан, положение куба в пространстве меняются — это несущественные признаки. Учащиеся должны на­учиться дифференцировать существенные и несущественные при­знаки куба. Это требует от учителя подбора кубов разнообразных как по размерам и цвету, так и по материалам, из которых они изготовлены, а также предметов обихода, имеющих форму куба (тумбочка, шкатулка, аквариум, ящик). Ученики убеждаются, что число граней, ребер и вершин остается постоянным, грани всех кубов — квадраты, ребра — отрезки, равные между собой.

Тут же рассматриваются различные по размеру, цвету, материалу брусы: каждый ученик рассматривает 2—3 разных бруса. Учи­тель просит назвать признаки, одинаковые для всех брусов: ко­личество граней, ребер, вершин, а также признаки, которыми брусы могут отличаться друг от друга (длина ребер).

Оборудование таких уроков потребует больших усилий со сто­роны педагога, так как каждый ребенок должен получить модели геометрических тел для практической работы по измерению и изу­чению свойств их элементов. Учителю, преподающему математику в V классе, могут помочь учащиеся старших классов, которые изго­товят модели кубов и иных прямоугольных параллелепипедов на уроках труда в картонажно-переплетной мастерской.

В VII классе школьников знакомят со смежными и противо­положными гранями. Дети уже знают, что каждое ребро куба (бруса) принадлежит двум граням, значит, ребро у них общее. Две грани, имеющие общее ребро, называются смежными гранями. Учащимся могут быть предложены следующие задания: показать ребро и две грани, для которых оно является общим, назвать эти грани; показать две смежные грани и их общее ребро; показать грань и все грани, с ней смежные. «Вот грань,— говорит учи­тель,— покажите и подсчитайте грани, смежные с ней. Сколько граней, смежных с данной, и почему?» Значит, признаком смежных граней является наличие общего для них ребра. Отсюда очень легко вывести определение противоположных граней — это грани, которые не имеют общих ребер. Самостоятельно найти такие грани учащимся трудно. Учитель показывает грань и просит найти грань, ей противо­положную (по аналогии с противоположными сторонами прямо­угольника).

На каждой грани нужно записать ее «номер». Например, нижнее основание — № 1, верхнее — № 2, боковые грани — № 3, 4, 5, 6.

В этом случае учителю легче вести беседу со школьниками. Так, он просит найти грань № 3 (боковая грань) и назвать грани, с ней смежные (№ 1, 2, 4, 6), или назвать грань, противоположную грани № 3 (грань № 5). Ученики должны показывать смежные и противоположные стены класса, заранее установив, что они явля­ются гранями бруса (куба).

При изучении прямоугольника учащиеся научились различать смежные и противоположные стороны этих фигур. А при изучении геометрических тел (куба, бруса) они знакомятся со смежными и противоположными гранями. Проводятся упражнения на диффе­ренциацию смежных и противоположных сторон, граней.

Смежные стороны имеют общую вершину, смежные грани имеют общее ребр