Построение отрезков заданной длины
Сначала учащиеся учатся строить отрезки заданной длины с помощью масштабной линейки, не имеющей оцифровки. Последовательность работы: 1) провести прямую; 2) отметить на ней точку — начало отрезка; 3) нулевое деление линейки совместить с этой точкой и, отсчитав от нее заданное количество сантиметров, отметить точку — конец отрезка; 4) соединить точки по линейке цветным карандашом и назвать длину полученного отрезка. Когда учащиеся научатся вычерчивать отрезки заданной длины, можно будет приступить к работе с масштабными линейками, где сантиметровые деления обозначены числами.
Учащиеся показывают на линейке указанное учителем число сантиметров и приступают к построению отрезка. Перед выполнением задания всегда обсуждается ход работы. Так, если требуется измерить отрезок, то один или двое учеников рассказывают, как это задание выполняется. Нужно приложить край линейки к отрезку так, чтобы нулевой штрих линейки совместился с началом отрезка. Затем посмотреть, сколько сантиметров содержится в отрезке. Если предстоит построить отрезок заданной длины, то учащиеся находят на линейке нулевое деление и деление, соответствующее заданной длине. Показывают эти деления на линейке, изображают точками на произвольной прямой начало и конец отрезка, а затем соединяют эти точки с помощью линейки (более жирной линией).
Упражнения по измерению и построению отрезков должны быть на этом этапе повседневными.
Уже в начале обучения в I классе дети знакомятся с понятиями: столько же, одинаковые, равные. При работе с отрезками эти понятия закрепляются. Учащимся предлагаются задания (II класс):-«Построить отрезок, в котором уложится столько же сантиметров, сколько в данном; начертить отрезок, равный данному (или такой же длины)».
Для построения таких отрезков (одинаковых, равных) может быть использован циркуль в качестве измерителя. Учащиеся раздвигают ножки циркуля на длину отрезка, а затем на произвольной прямой ставят ножку циркуля в произвольную точку (начало отрезка) и грифелем отмечают конец отрезка; убрав циркуль, соединяют полученные точки по линейке (усиливая изображение отрезка).
Во II классе большинство детей должно овладеть приемами вычерчивания отрезков и измерения их с помощью масштабной линейки.
На втором году обучения работа с линейкой продолжается. Следует расширить практику использования линейки не только при построении и измерении отрезков большой длины, но и новых вариантов отсчета заданного расстояния (наиболее часто в трудовой, учебной деятельности линейка бывает необходима для отсчета заданного расстояния от края листа бумаги, от края куска ткани и т. д.).
Поэтому во II классе наряду с повторением всех уже известных учащимся приемов работы следует предложить и новые, например отсчет заданного количества сантиметров от края детали, имеющей форму квадрата, любого прямоугольника (построение рамки, стороны которой параллельны краям заданного квадрата, прямо угольника). Для этого потребуется обучить учащихся отсчитывать заданное количество сантиметров от данного деления справа налево, сверху вниз, снизу вверх (рис. 2). Например, учитель просит найти и показать по линейке штрих, обозначенный числом 15, а затем отсчитать Назад (по направлению к нулю) несколько сантиметров; определить, сколько сантиметров содержится между штрихами 15 см и 12 см, 15 см и 10 см и т. д.
После того как учащиеся научатся отсчету сантиметров в обратном направлении (к нулю), учитель предлагает детям отметить самим на квадрате или прямоугольнике от каждой стороны по 3 см: I см от правой боковой стороны (3 см — 0 см), 3 см от нижней стороны вверх (0 см — 3 см) и 3 см от верхней стороны вниз (0 см — 3 см). Через полученные точки проводятся прямые.
Задания по изучению действий с отрезками следует связывать с арифметическим материалом. Например, построить один отрезок длиной 6 см, а другой — на 3 см длиннее (короче) — II класс, в 3 раза длиннее (короче) — III класс. Учащиеся вычисляют длину второго отрезка и чертят его под первым. Для проверки правильности построения надо сравнить длины двух отрезков.
Ломаная линия
В IV классе учащиеся знакомятся с ломаной линией.
Чтобы они лучше запомнили термин ломаная линия, можно взять палочку и переломить ее 1—2 раза или сложить несколько раз узкую полоску бумаги — получили ломаную линию. Ломаная линия состоит из двух или большего количества отрезков, расположенных так, что конец одного отрезка служит началом другого. Удобно показать ломаную, согнув в нескольких местах проволоку или раздвинув складной метр. Затем следует показать ломаную линию на чертеже. Элементами ломаной линии являются отрезки и вершины, углы. Отрезки,


 из которых состоит ломаная линия, могут иметь различную длину и положение.
из которых состоит ломаная линия, могут иметь различную длину и положение.
Для сознательного усвоения признаков ломаной линии можно предложить учащимся работу с таблицами, например с таблицей, на которой изображена ломаная линия из пяти отрезков и пять отдельных отрезков, которые равны звеньям ломаной линии и имеют те же положения на плоскости. Закрывая на таблице все звенья ломаной, кроме одного, учитель показывает детям, что ломаная состоит из отрезков. Они пересчитывают отрезки. После этого учитель обращает внимание учеников на пять отдельных отрезков, расположенных в том же положении, что и отрезки ломаной линии. Дети пересчитывают их. Отрезков тоже пять. Количество отрезков одинаковое, и если отрезки ломаной и данные отрезки соответственно равны по длине, то длина ломаной и сумма длин отдельных отрезков равны. Учитель просит определить сходство и различие между ломаной линией из пяти отрезков и пятью отрезками.
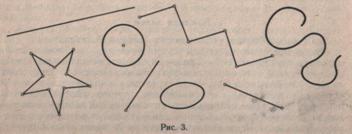
После знакомства с ломаной линией ученикам предлагаются задания на дифференциацию известных им линий. На таблицах (рис. 3), на доске, на поверхности окружающих предметов учащиеся выделяют и называют линии. Разного вида линии вычерчиваются в тетрадях.
В IV классе учащиеся знакомятся с замкнутыми и незамкнутыми линиями. Незамкнутая ломаная линия имеет начало и конец (так же как отрезок прямой), замкнутая не имеет ни начала, ни конца. Учитель сообщает учащимся, что если соединить начало и конец незамкнутой ломаной линии отрезком, то получится замкнутая ломаная линия. Если дана замкнутая ломаная линия, то достаточно отбросить один отрезок, чтобы она стала незамкнутой.
Учащиеся приводят примеры замкнутых и незамкнутых линий на окружающих их предметах.
Особое внимание следует уделить изучению многоугольников. На моделях и чертежах границы многоугольников выделяются цветом. Учащиеся убеждаются, что границы многоугольников — это замкнутые ломаные линии. Поэтому уместно проводить работу по определению числа отрезков в ломаных линиях, по конструированию ломаных линий из палочек, меняя вид линий и количество от-
|
резкое, из которых они состоят. Полезно ставить вопросы, развивающие пространственное воображение учащихся, например: «Представьте себе треугольник. Какая фигура образуется, если убрать одну сторону? Как нужно изменить чертеж треугольника, чтобы из треугольника получить четырехугольник?» И т. д.
Параллельно с замкнутыми, незамкнутыми ломаными учитель знакомит школьников с замкнутыми, незамкнутыми кривыми линиями.
Необходимо проводить упражнения на дифференциацию замкнутых и незамкнутых ломаных и кривых линий. Например, окружность, овал — кривые замкнутые линии, границы многоугольников — ломаные замкнутые линии, дуга — незамкнутая кривая линия.
Для вычерчивания кривых целесообразно пользоваться чертежными лекалами, которые могут быть изготовлены в школьных мастерских.
В V классе впервые вводится буквенное обозначение отрезков, ломаных линий и многоугольников. Для этого отбираются те латинские буквы, которые пишутся и произносятся одинаково с буквами русского алфавита (A, D, О, М, К, Е), а также буквы В, С, S, Р, К, V.