Связь геометрического материала в курсе математики с материалом других учебных предметов

Как уже говорилось выше, на уроках наглядной геометрии учи­тель развивает пространственные и геометрические представления учащихся, учит различать геометрические фигуры, знакомит с их свойствами, учит решать задачи геометрического содержания. Не­обходимо, чтобы геометрические знания учащиеся могли использо­вать в повседневной жизни, при изучении других учебных предме­тов, на уроках ручного и профессионального труда, в своей будущей трудовой деятельности.

Учитывая, что умственно отсталые дети испытывают большие трудности в использовании знаний в новой ситуации, в практической и трудовой деятельности, на уроках математики при изучении гео­метрического материала надо создавать ситуации, близкие к жизнен­ным, где учащиеся могли бы актуализировать имеющиеся геомет­рические знания и правильно их применять.

С одной стороны, при изучении почти каждого общеобразователь­ного предмета во вспомогательной школе можно найти применение знаниям по наглядной геометрии. С другой стороны, в содержание занятий по наглядной геометрии нужно включать материал из дру­гих учебных предметов, т. е. из других областей знаний

Изучение геометрического материала должно быть тесно связано, в первую очередь, с арифметическим материалом.

Например, уже в I классе при изучении чисел первого десятка

при знакомстве с образами геометрических фигур учитель может широко использовать эти фигуры в качестве дидактического мате­риала для счета, закрепляя при этом их названия.

Во II классе, когда учащиеся работают над различением элемен­та фигур, можно начать моделировать фигуры из палочек.

В III классе учащиеся получают представление о сантиметре Как единице измерения длины и знакомятся с измерением отрезков и сантиметрах. Полоску длиной 10 см, разделенную на 10 равных частей, можно использовать в качестве пособия для формирования представлений о натуральном числе и участке натурального ряда чисел (числовой луч). Масштабная линейка длиной 20 см (II класс), а затем и 100 см (III класс) может быть также использована в ка­честве пособия при формировании представлений о натуральных числах и их свойствах, числовом луче в пределах 20 и 100.

При формировании представлений о долях единиц, о дробях ши­роко используются геометрические фигуры и тела — круг, прямо­угольник, отрезок, куб, шар. Геометрическая фигура или тело при­нимается за единицу и делится на равные части, каждая из которых — доля, несколько долей — дробь.

При решении арифметических задач геометрические фигуры (от­резок, прямоугольник, круг и др.) служат средством наглядности для демонстрации зависимости между данными, а также между дан­ными и искомой величинами. Составляются схемы, графики, диаг­раммы, иллюстрирующие содержание математических задач.

При изучении геометрических величин (длина, площадь, объем) объектами измерений становятся геометрические фигуры.

Измеряются отрезки, стороны многоугольников, ребра геомет­рических тел. Учащиеся убеждаются в том, что длина отрезка — это число, полученное при укладывании единичного отрезка (1 мм, 1 см, I дм, 1 м). Это же относится и к измерению расстояний.

Учащиеся должны получить понятие о том, что площадь фигуры измеряется площадью единичного квадрата, принятого за единицу измерения площади, и число таких квадратов, которое уложится на данной фигуре, есть площадь фигуры. Объем же геометрического тела измеряется с помощью единичного куба, причем это тоже чис­ло; оно показывает, сколько единичных кубов уложилось в данном геометрическом теле. Учащиеся должны получить значительный опыт такого непосредственного измерения длины, площади, объема с по­мощью единиц измерения, прежде чем перейти к знакомству с фор­мулами вычисления площадей геометрических фигур и объемов геометрических тел.

Как измерять длину, площадь, объем, следует показать на следую­щих единицах измерения: 1 см, 1 см², 1 см³ или 1 дм, 1 дм², 1 дм . В этом случае учащиеся без особых затруднений осуществляют пере­нос полученных знаний и навыков на новые единицы измерения.

На уроках рисования учащиеся используют знания формы, вза­имного расположения предметов, а также представления о точке, линиях, их пересечении с целью более глубокого изучения предме­тов и правильного выполнения рисунка и расположения его на листе бумаги.

Особенно широко знания геометрического материала приме­няются в декоративном рисовании, где учащиеся выполняют орна­менты в фигурах различной формы — квадрате, круге, прямоугольни­ке, бордюры из геометрических фигур. На этих уроках учитель имеет возможность закрепить знания названий геометрических фигур, их свойств, расположения одной фигуры относительно другой.

Например, в V классе учащиеся рисуют орнамент в круге — на перпендикулярных диаметрах круга предусматривается построение четырех овалов-лепестков. Прежде чем выполнять такой рисунок, учитель рисования обязательно должен восстановить сведения о круге, овале, рассказать, как найти центр круга, если он рисуется по трафа­рету, сравнить окружность и овал.

С другой стороны, на уроке математики учитель должен обяза­тельно попросить детей вспомнить тот рисунок, который они выпол­няли на уроке рисования. Желательно, чтобы они в этот момент от­крыли альбом по рисованию. Надо, чтобы учащиеся выделили на рисунке все знакомые им геометрические фигуры, т. е. дали полный анализ рисунка с использованием своих геометрических знаний: по­казали плоскость, линии, точки, отрезки, назвали другие фигуры. При таком проведении уроков ученики убедятся во взаимосвязи знаний, полученных ими при изучении различных учебных предметов. На уроках физкультуры также можно использовать геометри­ческие знания, закреплять их и совершенствовать. Например, за­крепить пространственные представления учащихся, выражаемые словами: налево, направо, вперед, назад, вверх, вниз, далеко, близко и т. д.

На уроках географии также используются и закрепляются гео­метрические знания, умения и навыки.

Изучение формы Земли, понятия масштаба, плана, вычерчива­ние плана невозможно без геометрических знаний, без овладения измерительными и чертежными умениями и навыками, умением пользоваться линейкой, циркулем.

Например, от учащихся требуется начертить план класса. Они устанавливают, какую форму имеет пол классной комнаты. С этой целью измеряется длина и ширина класса, следовательно, актуали­зируются знания о четырехугольниках (квадрате, любом прямо­угольнике) и их свойствах. Далее выбирается масштаб, устанавли­ваются размеры прямоугольника, и учащиеся приступают к его по­строению.

Геометрические знания используются и на уроках естествозна­ния. Например, без знания учащимися геометрии учитель естест­вознания не сможет им объяснить, какую форму имее1 i рядка, клумба для цветов, газон и т. д.

На уроках ручного и профессионального труда учащиеся встре­чаются с различными геометрическими фигурами, пользуются ли­нейкой, чертежным треугольником, транспортиром циркулем.

Как правило, работа над любым изделием начинается с черте­жа, а в основе любого чертежа лежит прямоугольник, в частности квадрат, иногда круг. Чертеж может создаваться на бумаге (изготовление выкройки), на плоской поверхности заготовки (разметка).

Квадрат и прямоугольник вычерчиваются приемами, не зависящими от формы того куска плоскости, на котором создается чертеж; не­редко, наоборот, опорой для построения чертежа (отправными точками) служат края листа бумаги, края заготовки (когда их форма прямоугольная, в частности квадратная). В первом случае учащиеся не могут обойтись без чертежного треугольника, во втором случае им недостаточно одной линейки, когда они от всех сторон предложенного им листа (пластины, плитки) прямоугольной формы откладывают заданное количество сантиметров (миллиметров) (см. с 51, рис. 2). После построения прямоугольника (квадрата) дети проверяют точность построения чертежа, измеряя стороны, углы или перегибая (если возможно) чертеж по диагонали, например салфетку квадратной формы.

При создании выкроек на занятиях по швейному делу не всегда требуется построение прямоугольника (квадрата), иногда достаточно построить прямой угол, на сторонах которого от вершины откладываются заданные отрезки. Например, для построения на чертеже линии горловины учащиеся от вершины прямого угла откладывают равные отрезки, соединяют по линейке их концы, находят середину отрезка (измеряют его длину и делят полученное число на два), а затем проводят луч из вершины угла через полученную точку (се­редину), т. е. получают биссектрису прямого угла (рис. 1).

Во многих случаях линии чертежа (отрезки) делятся пополам, на 3, 4 равные части (швейное, столярное дело). Встречаются также параллельные и перпендикулярные прямые линии (проводятся «на одном и том же расстоянии друг от друга» или «под прямым углом Друг к другу»).

В швейном, слесарном, столярном деле встречаются изделия, имеющие форму круга (салфетка), цилиндра (коробка цилиндри­ческой формы, изделия, получаемые при работе на токарном станке) и др. Чертежи таких изделий выполняются с помощью циркуля (ок­ружность, круг).

С предметами, имеющими ту или иную геометрическую форму, учащиеся имеют дело в слесарной, столярной, картонажно-переплетной мастерских. Так, учащиеся изго­тавливают куб, любой прямоугольный па­раллелепипед, конус, пирамиду, т. е. все re тела, которые должны изучаться на уроках геометрии.

Программы ручного, профессионального труда содержат геометрический ма­териал, который есть и в программе по математике, но изучается он не в одно и то же время. Чаще всего на уроках труда учащиеся встречаются с теми или иными геометрическими знаниями, рань­ше, чем на уроках математики. На­пример, с геометрическими телами учащиеся работают на уроках слесарного дела в VIIклассе, тогда как на уроках математики более подробно изучают эти тела в VIII классе.

В связи с этим преподаватели труда должны строго придерживаться методики, терминологии, единых приемов построения и обозначения чертежей, правил при использовании измерительных и чертежных инструментов, принятых в математике, чтобы оградить изложение материала от логических дефектов и избежать угрозы переучивания учащихся в VIII классе.

Программа по слесарному делу содержит материал, который выходит за пределы геометрических сведений, включенных в програм­му по математике. Разумеется, эти сведения носят не столько тео­ретический, сколько прикладной характер. Например, вычисляется конусность детали: разность диаметров усеченного конуса делится на длину образующей конуса. Эти сведения носят специфический характер, поэтому они должны изучаться исключительно на заня­тиях по слесарному делу.

Для установления более тесной взаимосвязи между уроками ма­тематики и уроками труда учитель математики, в свою очередь, дол­жен чаще использовать наглядные пособия, измерительные инстру­менты, которые применяются на уроках труда, приводить больше примеров, задач, связанных с деятельностью детей на этих уроках.

Например, на урок математики учитель приносит изделия, из­готовленные учащимися на уроках труда (салфетку, наволочку, во­ротничок, коробку, деталь и т. д.). Учащиеся должны в этих пред­метах узнать уже знакомые им геометрические формы, установить их размеры, определить, сколько материала пошло на их изготовле­ние, и т. д. Для снятия размеров они используют линейку, нулевой штрих которой совпадает с началом линейки, слесарный и столяр­ный угольник, измеритель и т. д.

5. ОСНОВНЫЕ СРЕДСТВА, МЕТОДЫ И ПРИЕМЫ
ИЗУЧЕНИЯ ГЕОМЕТРИЧЕСКОГО МАТЕРИАЛА.
ПУТИ ФОРМИРОВАНИЯ ГЕОМЕТРИЧЕСКИХ ПРЕДСТАВЛЕНИЙ

Успех обучения наглядной геометрии во вспомогательной школе, преодоление трудностей в усвоении геометрического материала уча­щимися во многом зависит от правильного использования средств, методов и приемов обучения.

Обучение геометрии во вспомогательной школе должно быть на­глядным и действенным. Формирование пространственных и геомет­рических представлений у учащихся вспомогательной школы воз­можно только через непосредственное восприятие материальных моделей геометрических фигур, предметов окружающей действитель­ности. Переход к использованию чертежей и таблиц должен осу­ществляться постепенно и в доступной, упрощенной форме.

Все это требует от учителя вспомогательной школы необходи­мого оснащении уроков математики, особенно тех, на которых изу­чаются вопросы наглядной геометрии, наглядными пособиями и ди­дактическим материалом.

В качестве наглядных средств могут использоваться модели геометрических фигур и тел разных размеров, цвета, изготовленные из

различных материалов (картонные, бумажные, пластмассовые, деревянные, металлические и т. д.), плакаты с изображением фигур, реальные конкретные предметы, которые по форме тождественны или имеют сходство с изучаемыми геометрическими фигурами, чертежи всех изучаемых геометрических фигур и тел, единицы мер длины площади, объема (там, где возможно, в натуральную величину), таблицы соотношения единиц мер, таблицы измерения площадей, объемов, площадей боковых и полных поверхностей фигур, наборы игр (геометрические мозаики, домино, лото, конструкторы и т. д.), диафильмы.

Преподавание элементов геометрии невозможно сделать действенным, если учащиеся только наблюдают работу учителя или одного из товарищей с наглядными пособиями. Каждый ученик должен на уроке математики самостоятельно работать с раздаточным гео­метрическим материалом. Поэтому необходимо, чтобы наборы раздаточного дидактического материала находились и у учащихся, и у учителя. Наряду с геометрическими фигурами и телами в качестве раздаточного материала используются полоски бумаги, палочки раз­ной длины, пластилин.

При изучении геометрического материала широко применяются измерительные и чертежные инструменты (как классные, так и индивидуальные): линейка, рулетка, циркуль, чертежный треугольник, транспортир. При изучении отдельных тем полезно использовать модели раздвижного угла, многоугольников, единиц измерения пло­щади, объема и др.

Выбор методов и приемов, применяемых при изучении геомет­рического материала, должен определяться его характером, индиви­дуальными возможностями умственно отсталых детей и коррекционными задачами учебно-воспитательного процесса во вспомогатель­ной школе.

В младших классах вспомогательной школы учащиеся должны накопить определенный запас геометрических представлений. Это­му способствует использование метода наблюденийпри ознакомле­нии с геометрическими образами. Учащиеся рассматривают модели геометрических фигур, разнообразные предметы, имеющие форму них геометрических фигур, их изображения.

Объекты наблюдений должны быть ясно видны каждому ученику класса, существенные признаки фигур выделены цветом, модели фи­гур или чертежи тщательно выполнены. Они должны вызывать поло­жительные эмоции у учащихся, т. е. не должна быть забыта эсте­тическая сторона при восприятии учебного материала на уроках.

Выбор объекта наблюдений определяется целями урока. Напри­мер, чтобы сформировать представление о круге, в качестве объек­та наблюдения выбирается сначала круг, имеющий признаки, одинаковые с данным образцом, затем круги, отличающиеся от образца несущественными признаками (цветом, размером, материалом, из ко­торого они изготовлены).

Чтобы учащиеся могли выделить круг из числа других геометрических фигур, объектами наблюдений следует брать не только кру­ги, но и другие геометрические фигуры.

Используя метод наблюдения при сообщении новых знаний, учи­тель заранее определяет, что учащиеся должны наблюдать, на ка­кие признаки они должны обратить внимание, и на основе органи­зации наблюдения ведет их к определенным выводам. Желательно, чтобы в формулировке выводов принимали участие сами учащиеся. Учитывая, что наблюдательность у умственно отсталых школьни­ков снижена, достичь желаемых результатов возможно лини, при руко­водстве наблюдениями учащихся, т. е. в случае, когда учитель своими вопросами организует и направляет наблюдения школьников на те существенные признаки, которые отличают одну фигуру от другой. Таким образом, метод наблюдений сочетается с методом беседы. Руководящая роль учителя при организации наблюдении неоди­накова в младших и старших классах. Чем старше дети, тем выше их самостоятельность и активность.

Специальные психологические и педагогические исследования и опыт обучения учащихся вспомогательной школы показывают, что практическая деятельностьребенка (его работа руками) е предме­том позволяет глубже и более разносторонне изучить его призна­ки, лучше запомнить характерные особенности, чем голыш при зри­тельном и слуховом восприятии. Следовательно, метод наблюденияпри изучении геометрических фигур надо сочетать со словом учи­теля и практической деятельностью самихучащихся. На уроках ма­тематики при изучении геометрического материала оправдали себя следующие виды практической деятельности: аппликационные работы, лепка, обводка, раскрашивание, штриховка, вырезывание из бумаги, работы по конструированию и моделированию. Из палочек учащиеся выкладывают геометрические фигуры треугольник, четырехуголь­ник и другие многоугольники, из геометрических фигур моделируют домик, дерево, флаг, машину, вертолет и пр. Школьники выполняют измерения, построения и т.д. Самостоятельность и интимность уча­щихся должны быть максимальными.

При изучении геометрического материала во вспомогательной школе большое место отводится дидактической игрекак методу обу­чения. (Перова М. Н. Дидактические игры и занимательные упражнения на уроках математики во вспомогательной школе. - М , 1976.) Игры повышают интерес к изучаемому материалу, разнообразят виды заданий и упражнений, способствуют закреплению названий фигур, их систематизации и глубокому изучению свойств, закреплению их существенных признаков. Игра позволяет преподнести изучаемый материал в занимательной форме, снижает детскую утомляемость. Наиболее часто употребляемые дидактические игры геометри­ческие лото, домино, мозаика, игры с конструктором, игры вида «Что изменилось?», «Какая фигура спрятана в мешочке?", "Угадай, какую фигуру я спрятала», «Дострой фигуру», зрительные и слуховые диктанты в занимательной форме и т.д.

Метод работы с учебникомпри изучении геометрического мате­риала остается основным методом обучения как и младших, так и в старших классах. Учебник нередко выступает в качестве источника знаний. По учебнику подбираются задачи и другие задания, которые способствуют закреплению знаний, выработке практических уме­нии и навыков.

При обобщении изученного материала можно дать учащимся задание по учебнику найти сходство, различие в определении двух фигур, сравнение их, вычисление периметра, площади, объема и т. д. Изучение свойства геометрических фигур должно проходить вначале опытным путем.Работая с разнообразными предметами геометрической формы, моделями фигур, измеряя, накладывая одну фигуру на другую, сравнивая их, учащиеся выявляют их существенные признаки, не зависящие от материала, цвета, размера, массы, положения на плоскости или в пространстве и т.д.

Учитель строит работу так, чтобы у учащихся формировались навыки индуктивного мышления, воспитывалось умение делать простейшие индуктивные умозаключения на основе наблюдений и активной практической деятельности. Осуществляется это через фор­мирование приемов умственных действий, таких, как анализ и синтез, сравнение, абстрагирование, обобщение. Уже при первоначальном ознакомлении с геометрическими фигурами дети выполняют умствен­ные операции анализа и синтеза. В этот период они знакомятся с анализом фигур, выделяя существенные и несущественные признаки. Например, для прямоугольника существенно то, что он — четырех­угольник (четыре угла) и все углы у него — прямые. Несущественно его положение на плоскости листа бумаги, классной доске, размеры сторон. Следовательно, положение его на плоскости надо постоянно и сменять, предъявлять прямоугольники с различной длиной сторон. Очень важно при изучении геометрических фигур варьировать несущественные признаки геометрических фигур, подчеркивая при лом, что существенные признаки остаются неизменными. Напри­мер, при изучении свойств квадрата с учащимися проводится лабораторно-практическая работа, которая состоит в следующем.

Каждый ученик получает модель квадрата: учитель обращает внимание детей на то, что каждый из них получил разные по цвету, размеру, изготовленные из разного материала четырехугольники. Предлагается установить вид углов четырехугольника (квадрата), Устанавливается, что, несмотря на то что у всех школьников квад­раты разные, углы всех фигур прямые. Далее учитель просит из­мерить стороны. Учащиеся убеждаются, что стороны одного и того же квадрата равны. Затем учитель показывает квадраты разных цветов (желтые, зеленые и т. д.), разных размеров (большие и маленькие), изготовленные из разных материалов (деревянные, пластмассовые и т.д.), в разном положении и обращает внимание на то, что все несу­щественные признаки не влияют на основные свойства фигуры. Однако если изменить хотя бы один существенный признак в квадрате (и в любой другой фигуре), то получится уже другая фигура. На модели квадрата, сделанной из палочек одинаковой длины, учащиеся пыта­ются изменить существенные признаки, например длину одной или двух сторон, величину угла. Получается уже новая фигура. Различные упражнения по моделированию фигур из палочек, полосок бумаги помогают учащимся лучше усвоить основные свойства фигур, понять существенные признаки, которые лежат в основа определения фигур.

Полезно вначале давать упражнения и задания практического характера. Например, предложить учащимся из палочек выложить прямоугольник и выполнить такие операции: «Сделайте острым один из углов прямоугольника. Какая фигура получилась? Почему эту фигуру нельзя назвать прямоугольником?» Еще например: "Возьмите модель раздвижного треугольника (остроугольного) и измените угол в остроугольном треугольнике так, чтобы треугольник стал угольным (тупоугольным)». После этого учители может спросить учеников, опираясь только на их воображение, как при изменении того или иного признака изменилась фигура. Например: " Если в равностороннем треугольнике сделать короче одну сторону, то какой треугольник получится?»

Важно, чтобы и сами учащиеся, особенно в старших классах, варьировали несущественные признаки при постоянстве существенных признаков и приводили примеры, когда изменение существенных признаков приводит к замене вида фигуры. В этих случаях полезны упражнения с моделями фигур, выполненными из проволоки. На них можно быстро изменить меру угла, длину стороны. Учащиеся смогут наблюдать, как изменения свойств фигуры отражаются на фигуре в целом. Полезны практические упражнения с палочками на достраивание фигур.

На занятиях по геометрий необходимо работать с конструктором Эта работа развивает воображение, смекалка, пространственные представления.

Учитывая несовершенство мыслительных процессов анализа и синтеза у умственно отсталых детей, им следует помочь создать определенную схему анализа фигур. Например: вид и число углов, длина сторон и их число, название фигуры.

В старших классах, кроме умения выделим. подсчитать число элементов фигуры, от учащихся требуется описать свойства этих фигур (равенство всех сторон и всех углов квадрата, равенство противоположных сторон и всех углов — в любом прямоугольнике и т. д.). Пользуясь такой схемой, учащиеся запоминают ее, и им уже не требуется задавать дополнительных вопросов. В старших классах учащиеся должны уметь назвать линии, которые можно провести в фигуре (радиус, хорду, диаметр, диагональ, высоту и т.д.).

Одна из задач методики изучения геометрического материала состоит в систематическом осуществлении первоначального ознакомления учащихся с классификациейфигур.

Таким образом, при ознакомлении с новым материалом учитель подводит учащихся к обобщению. Обобщение это может выражаться в выводе правила, формулировке свойства и т.д.

Широко используется и дедуктивный путь познания: подведение частного положения под общее. Например, чтобы определить периметр той или иной геометрической фигуры, нужно опираться на знание общего характера: периметр — это сумма длин сторон той или иной фигуры. Зная это определение, учащиеся должны уметь использовать его при вычислении (посредством измерения сторон) периметра любой конкретной фигуры.

Подведение частного факта под правило представляет большую трудность для умственно отсталых учащихся.

Преодолению этих трудностей способствует требование учителя самим приводить примеры, делать зарисовки, чертежи, подбирать наглядный материал для иллюстрации того или иного правила, свойст­ва, общей формулы и т.д.

Значительное место при изучении наглядной геометрии как в младших, так и в старших классах отводится приему сравнения. Со­поставляются и противопоставляются плоские фигуры (круг —мно­гоугольник, квадрат — треугольник, круг — окружность и т. д.), а также плоские и пространственные (квадрат — куб, круг — шар, прямоугольник — параллелепипед, их свойства и т. д.) из множества фигур выделяется множество многоугольников, множество линий и т. д. Это позволяет уточнить свойства фигур, их классификацию.

Приему сравнения надо учить. Целесообразно дать школьникам план, по которому они могут сравнивать фигуры.

Надо учитывать, что умственно отсталые дети нередко произ­водят сравнение не по соотносимым признакам, поэтому план помо­жет им правильно и последовательно осуществить сравнение фигур, не пропустить какого-либо признака.

Обучение сравнению должно пройти через несколько этапов.

На I этапе учитель проводит сравнение, а учащиеся лишь слу­шают и повторяют за учителем.

На II этапе учитель начинает сравнение, а учащиеся его продол­жают.

На III этапе сравнение ведется по плану под руководством учи­теля; план дается в форме вопросов.

На IV этапе сравнение проводится учащимися по плану самосто­ятельно.

На V этапе — самостоятельное сравнение.

К старшим классам учащиеся должны научиться осуществлять самостоятельное сравнение фигур.

Например, сравнение треугольников разных видов.

I этап.Сравнение проводит учитель. Он показывает модели разно­стороннего и равностороннего треугольников и говорит: «Эта гео­метрическая фигура имеет три угла и три стороны (показ первой фигуры). Эта фигура имеет тоже три угла и три стороны (показ вто­рой фигуры). Эти фигуры похожи. Это треугольники.

Сравниваю треугольники по длине сторон. Измеряю стороны пер­вого треугольника. Сравниваю длину сторон. Все стороны этого тре­угольника имеют разную длину. Измеряю стороны второго треуголь­ника. Сравниваю длину сторон. Две стороны имеют одинаковую длину.

Стороны первого треугольника имеют разную длину, а две стороны второго треугольника имеют одинаковую длину. Этим они непохожи. Первый треугольник разносторонний, второй — равнобедренный.

Сравниваю треугольники по видам углов. Определяю с помощью чертежного треугольника виды углов первого треугольника. Все углы острые. Определяю виды углов второго треугольника. Все углы острые. Этим треугольники похожи. Они оба остроугольные».

II этап.Учитель начинает сравнение, а ученик его продолжает: «Эта геометрическая фигура имеет три угла и три стороны, а эта... Этим фигуры... Это...»

Сравниваем треугольники по длине сторон. Длина сторон первого треугольника... Длина сторон второго треугольника... Этим треуголь­ники... Первый треугольник называется разносторонним, второй...

Сравниваем треугольники по видам углов. Первый треугольник имеет все острые углы, второй... Этим треугольники... Первый тре­угольник — остроугольный, второй...»

III этап.Сравнение ведется по плану под руководством учителя.
«Сколько углов у первой фигуры, сколько сторон? Сколько углов у второй фигуры, сколько сторон? Как называются эти фигуры?

Измерим длину сторон первого треугольника. Что можно сказать о длине его сторон? Измерим длину сторон второго треугольника. Что можно сказать о длине его сторон? Как называется первый тре­угольник, как называется второй треугольник?

Определим виды углов первого треугольника. Что можно ска­зать об его углах? Определим виды углов второго треугольника. Что можно сказать об его углах? Как называется первый треугольник, как называется второй треугольник?»

IV этап.Сравнение проводится учащимися самостоятельно по плану.

1) Стороны треугольников (количество, длина). Виды треуголь­ников.

2) Углы треугольников (количество, вид). Виды треугольников.

V этап. Сравнение проводится учащимися самостоятельно.

1) Сходство треугольников разных видов.

2) Различие треугольников разных видов.

При сравнении плохо дифференцируемых учащимися свойств прямоугольника и любого другого параллелограмма в IV классе можно предложить учащимся такую схему:

1) вид многоугольника; 2) углы, их число и свойства; 3) вер­шины, их число; 4) стороны, их число и свойства; 5) диагонали, их число и свойства; 6) высоты.

Характеризуя элементы фигур, их свойства, учащиеся должны назвать признак сходства или различия. Например: «У прямоуголь­ника, как и любого параллелограмма, 4 угла. В этом сходство фигур. У прямоугольника все углы прямые, у параллелограмма любого дру­гого вида два противоположных угла тупые, а два других острые. В этом различие прямоугольника и параллелограмма. У прямоуголь­ника и параллелограмма по 4 вершины. В этом их сходство. У прямо­угольника и параллелограмма другого вида по 4 стороны, противо­положные стороны этих фигур равны и параллельны. В этом сходст­во». И т. д.

Сравнение используется для дифференциации сходных по форме

фигур, для сопоставления и противопоставления видов одной и той же фигуры, например видов углов, треугольников, параллелограммов.

Известно, что в соответствии с требованиями программы, начиная С V класса, учащиеся знакомятся с буквенной символикой. Они обоз­начают буквами отрезки, углы, стороны фигур. Введение буквенной символики не только помогает различить фигуры и их элементы, Но и является одним из средств формирования обобщений, навыков сравнения. Учащиеся сравнивают с помощью буквенной символики отрезки, углы, устанавливая между ними отношения равенства и неравенства. Например, запись: 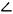АВС<90° — означает, что 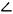АBC может быть любым углом, меньше прямого, т. е. любым острым углом. Здесь уже присутствует элемент обобщения.

Формированию обобщений у учащихся вспомогательной школы способствует и введение буквенной символики при обозначении пе­риметра, площади, объема, площади полной и боковой поверхности. Учащиеся старших классов овладевают приемами вычислений пери­метра, площади геометрической фигуры (параллелограмма, треуголь­ника), площади полной и боковой поверхности геометрического тела (параллелепипеда и др.).

Обучение учащихся элементам геометрии невозможно представить без систематической работы, обеспечивающей формирование навыков использования измерительных и чертежных инструментов, построения геометрических фигур, умения описывать процессы и ре­зультаты работ.Важным условием реализации является обеспечение сознательности выполнения действий учащимися и лишь на основании этого — достижение автоматизированных действий.

Учитель вспомогательной школы должен хорошо понимать, что успех в выработке любого навыка у умственно отсталого школь­ника может быть достигнут лишь при огромной затрате усилий как ученика, так и учителя. Автоматизация навыков требует системати­ческих ежедневных упражнений на уроках не только математики, но и других учебных предметов.

У большинства учащихся вспомогательной школы отмечается несовершенство моторики вследствие так называемых стертых ком­пенсированных паретических состояний, а нередко и явных физичес­ких недостатков (параличи, парезы, тремморы рук). Это затрудняет овладение навыками черчения и работы с измерительными и чер­тежными инструментами.

Учитель вспомогательной школы должен с I класса терпеливо, настойчиво и систематически проводить с учащимися работу по фор­мированию умений и навыков работы с инструментами. Например, в I классе учащиеся знакомятся с линейкой, учатся чертить прямые линии произвольной длины с помощью линейки.

Учитель должен показать, как держать линейку, как приложить ее к измеряемому объекту, от какого штриха производить измерение линейкой. Здесь недостаточно однократного фронтального показа приемов работы. Нужно подойти к каждому ребенку, буквально взять его руку и учить правильно держать линейку. Сначала учащиеся чертят произвольные прямые по линейке в разных положениях, затем

учатся с помощью линейки проводить прямую через одну точку, соединять точки, проводить прямую через две точки, затем изме­рять отрезки в сантиметрах и вычерчивать отрезки заданной длины. Во II классе навыки работы с линейкой совершенствуются, предъ­являются требования к качеству выполнения чертежей, учащиеся учатся чертить с помощью линейки по данным вершинам (точкам) геометрические фигуры (любой прямоугольник), а с помощью чер­тежного треугольника — углы.

Предварительно обсуждается последовательность выполнения практической работы, т. е. составляется план работы. Затем уча­щиеся выполняют построение. После этого они должны рассказать (дать отчет), как выполнили работу.

На последующих годах обучения учитель должен повышать тре­бования к качеству выполняемых чертежей, к точности построения. Например, уже в V классе учащиеся выполняют построение фигур по заданным размерам в миллиметрах. Формирование прочных навы­ков по измерению и построению фигур готовит учащихся к занятиям по профессиональному труду, к более успешному овладению трудо­выми навыками.

Чрезвычайно важно, чтобы объектами для измерения на уроках математики были не только модели геометрических фигур, чертежи, но и предметы окружающей действительности, предметы или детали предметов, взятые с уроков труда, изготовленные самими учащи­мися или их старшими товарищами. Это позволит теснее осуществлять межпредметные связи и связь преподавания математики с жизнью.

Выработка измерительных и чертежных навыков должна соче­таться с формированием умственных действий у учащихся. При этом любое действие ученика должно быть доведено до автомати­зированного навыка, однако каждое действие должно быть и объяс­нено учащимся.

При формировании измерительных и чертежных навыков можно выделить несколько этапов:

I этап— показ действия учителя с комментированием его вы­полнения;

II этап— выполнение этого действия учеником совместно с учителем или под его руководством и «проговаривание» приемов его выполнения в громкой речи;

III этап— самостоятельное выполнение действия учеником с последующим контролем учителя, умение объяснить (с помощью наводящих вопросов) приемы работы;

IV этап— автоматизация навыков путем многократного пов­торения действия. Умение самостоятельно объяснять приемы работы.

Выполнение измерительных и чертежных работ необходимо соче­тать с закреплением знаний учащихся. Этой цели служат задания, связанные с построением фи<