Основные надписи (гост 2104-80)

Оформление чертежей.

Форматы ( гост 2301-68)

ГОСТ 2.301-68 устанавливает размеры и обозначения форматов, на которых выполняются конструкторские документы.

Основных форматов 5, в обозначении формата входит буква А и арабская цифра, которая указывает сколько раз был разделен больший из форматов для получения данного.

Наибольший формат А0 - 1189х841; А1 - 594х841; А2 - 594х420; А3 - 297х420; А4 - 297х210.

Масштабы (гост 2302-68)

Масштабы. Отношения линейных размеров изображения на чертеже к действительным размерам называется масштабом. ГОСТ 2.302-68 устанавливает след.масштабы: уменьшения (1:2,1:2.5,1:(4,5,10,15,20,25,40,50,75,100,200,400,500,800,1000)), увеличения (2,2.5,4,5,10,20,40,50,100):1.

Линии черчежа(гост 2303-68)

Линии. ГОСТ 2.303-68 устанавливает 9 типов линий:Сплошная толстая основная, сплошная тонкая, сплошная волнистая, штриховая, штрих-пунктирная тонкая, штрих-пунктирная утолщенная, разомкнутая, сплошная тонкая с изломами, штрих-пунктирная с двумя точками тонкая.

Шрифт (гост 2304-81)

Шрифты. ГОСТ 2.304-81 устанавливает след. типы шрифтов: тип А- с наклоном и без, Б- с наклоном и без. Все надписи на чертеже наносятся под углом 75 градусов. h шрифтов- высота прописных букв, h письменных букв определяется h предыдущего меньшего шрифта. Существуют след.размеры шрифтов:2.5,3.5,5,7,10,14,20,28,40.

Основные надписи (гост 2104-80)

Страница 17,18 – лагерь.

Основные правила нанесения размеров (гост 2307-68)

Размеры 2.307-68

Нанесение размеров. Размерные числа наносят над размерной линией примерно посередине. На концах размерной линии наносят стрелки. Расстояние между размернымим линиями должна быть минимум 7мм, а от линии внешнего контура 10мм. размеры указываются в миллиметрах, без обозначения ед. измерения

При нанесении нескольких параллельных или концентрических размерных линий на небольшом расстоянии друг от друга размерные числа распологают в шахмотном порядке.

Размерные линии наносят вне контура изображеия и не допускают их пересечения. Нельзя использовать в качестве рамерных линий контуры, осевые, центровые и выносные линии

Не допускается повторять размеры одного и того же элемента на разных изображениях и надписях чертежа. ОБщее количество размеров должно быть минимальным, но достаточным для изготовления и контроля изделия.

Применять простые дроби для размерных чисел не допускается, за исключением рамеров в дюймах.

Кроме простых длин, наносятся и другие размерности, такие как: угловые рамеры, диаметры, радиусы, сферы,дуги, фаски, квадраты, уклоны и конусности. Для перечисленных размерностей перед самим размером ставится определенное графическое обозначение, соответствующее данному размеру.

Геометрические построения.

Сопряжения

Принято называть плавный переход одной линии в другую (прямой в дугу или дугу в др. дугу).

Общая для этих линий точка называется точкой сопряжения. Дуга окружности, при помощи которой осущесвляется плавный переход называется дугой сопряжения, а ее радиус - радиусом сопряжения.

В общем случае построение 2 сопряженных линий при заданном r сопряжения состоит из след.этапов:

1) проводят линию, параллельную данной, на расстоянии r сопряжения.

2) проводят линию, на расстоянии r сопряжения параллельную второй прямой.

3) отмечают точку пересечения проведенных линий (центр дуги сопряжения).

4) определяют точки сопряжения на 1-ой и 2-ой из сопряженных линий, при этом, если сопрягается прямая и дуга окружности для определения точки сопряжения нужно из центра дуги опустить перпендикуляр на прямую.

Если сопрягаются 2 дуги, то для определения точки сопряжения следует соединить прямой линией центры этих дуг. То на пересечении с 1-ой из дуг получится точка.

Построение уклонов и конусностей.

Уклон- наклон одной прямой линии к другой. Уклоном i прямой BC относительно AB называют отношение разности выот двух точек А и В к горизонтальному расстоянию l между ними или отношение катета AD к катету BC. i = h/l= AC/BC=tg(альфа)

Уклон обозначается знаком угла в обратную сторону и острый угол которого всегда расположен в сторону уклона.

КонусностьК - отношение разности диаметров D-d двух поперечных сечений конуса к расстоянию между ними l.

ПОстроение конусности 1:n относительно данной оси сводится к построению уклона 1:2n с каждой стороны оси. Конусность обозначается равнобедренным треугольником, лежащим на боку, острый угол которого направляют в сторону вершины конуса.

Изображение предметов на черчежах.

Виды.

Лагерь:173-180

Новичихина:66-80

Разрезы.

Разрезы разделяются, в зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций, на:

горизонтальные – секущая плоскость параллельна горизонтальной плоскости проекций.

вертикальные – секущая плоскость перпендикулярна горизонтальной плоскости проекций ;

наклонные –секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого .

В зависимости от числа секущих плоскостей разрезы разделяются на:

простые – при одной секущей плоскости ;

сложные – при нескольких секущих плоскостях.

Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций , и профильным, если секущая плоскость параллельна профильной плоскости проекций.

Разрезы называются продольными, если секущие плоскости направлены вдоль длины или высоты предмета и поперечными, если секущие плоскости направлены перпендикулярно длине или высоте предмета.

У начала и конца линии сечения, а при необходимости и у мест пересечения секущих плоскостей ставят одну и ту же прописную букву русского алфавита. Буквы наносят около стрелок, указывающих направление взгляда, и в местах пересечения со стороны внешнего угла.

Разрез должен быть отмечен надписью по типу «А-А» (всегда двумя буквами через тире).

Фронтальным и профильным разрезам, как правило, придают положение, соответствующее принятому для данного предмета на главном изображении чертежа. Горизонтальные, фронтальные и профильные разрезы могут быть расположены на месте соответствующих основных видов.

При ломаных разрезах секущие плоскости условно повертывают до совмещения в одну плоскость, при этом направление поворота может не совпадать с направлением взгляда

Разрез, служащий для выяснения устройства предмета лишь в отдельном, ограниченном месте, называется местным

Местный разрез выделяется на виде сплошной волнистой линией или сплошной тонкой линией с изломом. Эти линии не должны совпадать с какими-либо другими линиями изображения

Часть вида и часть соответствующего разреза допускается соединять, разделяя их сплошной волнистой линией или сплошной тонкой линией с изломом. Если при этом соединяются половина вида и половина разреза, каждый из которых является симметричной фигурой, то разделяющей линией служит ось симметрии

сложные – при нескольких секущих плоскостях

Сложные разрезы бывают ступенчатые, если секущие плоскости параллельны (например, ступенчатый горизонтальный разрез Б-Б, рис. 6), и ломанным, если секущие плоскости пересекаются (например, разрезы А-А).

Положение секущей плоскости указывают на чертеже линией сечения. Для линии сечения должна применяться разомкнутая линия. При сложном разрезе штрихи проводят также у мест пересечения секущих плоскостей между собой. На начальном и конечном штрихах следует ставить стрелки, указывающие направление взгляда

У начала и конца линии сечения, а при необходимости и у мест пересечения секущих плоскостей ставят одну и ту же прописную букву русского алфавита. Буквы наносят около стрелок, указывающих направление взгляда, и в местах пересечения со стороны внешнего угла.

Разрез должен быть отмечен надписью по типу «А-А»

При ломаных разрезах секущие плоскости условно повертывают до совмещения в одну плоскость, при этом направление поворота может не совпадать с направлением взгляда.

Если совмещенные плоскости окажутся параллельными одной из основных плоскостей проекций, то ломаный разрез допускается помещать на месте соответствующего вида . При повороте секущей плоскости элементы предмета, расположенные за ней, вычерчивают так, как они проецируются на соответствующую плоскость, с которой производится совмещение.

Сечения.

Новичихина: с 68стр.

Лагерь: с 190 стр.

Сечения - фигура, расположенная в плоскости, входит в стостав разреза или самосотоятельного изображения.

Сечения бывают вынесенные и наложенные. Наложенное сечение в виде детали и обводжят его тонкой линией, вынесенное сечение оформляют так же как и простой разрез, т.е. указывают направление взгляда стрелкой по типу А-А, Б-Б.

Аксонометрия( гост 2317-69)

Прямоугольная диметрия

Прямоугольная диметрия характеризуется тем, что коэффициенты искажения, определенные из выражения (1), и = w = 0,94, a v = 0,47. Определяют их следующим образом:

u²+(u/2)²+u²=2;

u² =8/9; u = w = (8/9)^1/2=0,94; v = 0,47.

В соответствии с ГОСТ 2.317—69 практические построения в прямоугольной диметрии следует выполнять пользуясь приведенными коэффициентами искажения: u = w=1и v = 0,5.

Расположение осей стандартной прямоугольной диметрии показано на рис. 162. Аксонометрический масштаб для прямоугольной диметрии будет М^A 1,06 : 1.

В прямоугольной диметрии равные окружности диаметра d, лежащие в координатных плоскостях хОу и уО, проецируются в равные эллипсы, большая ось которых 2а = 1,06d, а малая — 2b = 0,35d, если пользуемся приведенными коэффициентами искажения. Окружность, расположенная в плоскости xOz, проецируется в эллипс с осями: большая ось которых 2а¹ = 1,066d, малая ось — 2b¹ = 0,95d (рис. 163). Диаметры.окруж-

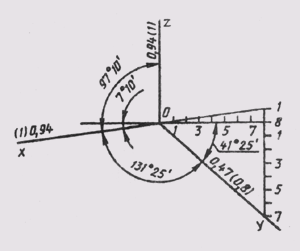
Рис. 162

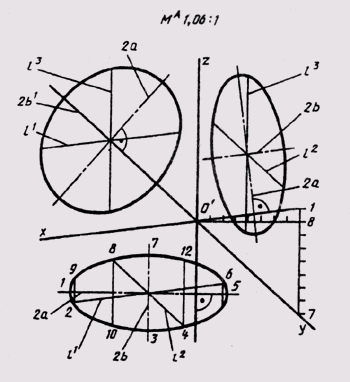
Рис. 163

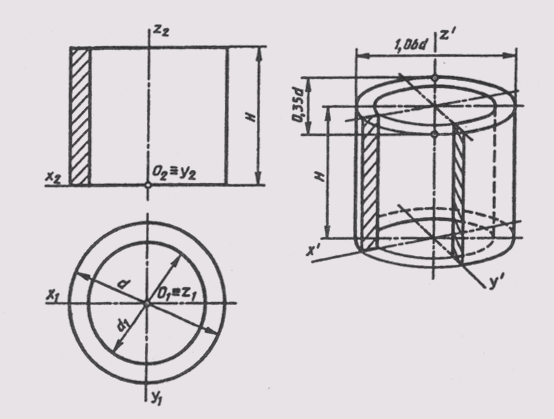
Рис. 164

ности, параллельные координатным осям, спроецируются в отрезки, параллельные осям диаметрии l¹ = l² = d; l = 0,5d, при этом || Ох; l² ||Оу; l³ || Oz.

Можно построить кроме указанных точек еще четыре точки, симметричные точкам, ограничивающим проекции диаметров, параллельных координатным осям. Тогда эллипс, как диметрию окружности, можно построить по его двенадцати точкам.

Изображение геометрических поверхностей в прямоугольной диметрии рассмотрим на примере построения стандартной прямоугольной диметрии прямого кругового цилиндра. На рис. 164 приведен пример комплексного чертежа полого цилиндра высотой Н c наружным d и внутренним d1диаметрами. Цилиндр расположим в натуральную величину в натуральной системе координат Oxyz, относительно которой построим диметрическую его проекцию. Как и в случае построения окружностей в изометрии, в диметрии также начнем построение фигуры с эллипсов верхнего и нижнего оснований цилиндра, которые являются изометрическими проекциями окружностей этих оснований. Окружности основания расположены в плоскостях, параллельных горизонтальной плоскости проекций, поэтому, пользуясь приведенными ранее правилами, определим, что большие оси эллипсов будут перпендикулярны оси Oz. Малые оси эллипсов совпадут с направлением оси Oz. Центры осей эллипсов нижнего и верхнего оснований расположены на расстоянии Я. Величины осей определяем в зависимости от величины наружного и внутреннего диаметров цилиндров. Построив эллипсы, приведем очерковые линии, касательные к внешним эллипсам.

Для наглядности построим вырез четверти цилиндра, построение которого видно из рис. 164. Направление штриховки выреза выберем, как показано на рис. 200. Невидимые линии покажем штриховыми линиями. Для наглядности такими же линиями покажем линии вырезанной части цилиндра. Видимые контурные линии наводят нужной толщиной.

162.gif

163.gif

164.gif

Начертательная геометрия.

Метод проекций

ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ

Основными видами проецирования являются центральное и параллельное. Центральное проецирование представляет собой общий случай проецирования геометрических образов из некоторого центра на плоскость.

Пусть задана плоскость П₁ и кривая линия k с точками А, В, С (рис.1.1).

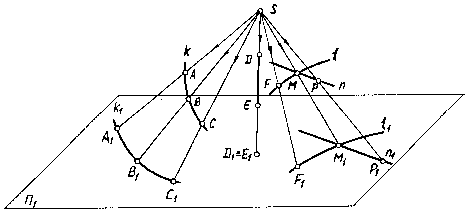Рис.1.1

Возьмем некоторую точку S, не лежащую в плоскости П₁. Через точку S и точки А, В, С кривой k проведем прямые до пересечения с плоскостью П₁ в точках A₁, B₁, C₁. Проведя таким образом через S и каждую точку кривой k прямые, получим в плоскости П₁ изображение k₁кривой k.

В соответствии с описанным построением введем следующие понятия:

S - центр проекций; П₁ - плоскость проекций; кривая k с точками А, В, С - объект проецирования; SА, SВ, SС - проецирующие лучи;A₁,B₁,C₁ - центральные проекции точек А, В, С; k₁ - центральная проекция кривой k. Рассматривая каждую пространственную фигуру как совокупность точек, можно сказать, что проекция фигуры представляет собой множество проекций ее точек.

Свойства центрального проецирования:

1. Любая точка (кроме S) проецируется на плоскость проекций в единственную точку (рис.1).

2. Каждой точке (A, B, C, D,...), принадлежащей какой-либо линии (кривой или прямой), соответствует проекция (A₁, B₁, C₁, D₁, ...) этой точки на проекции данной линии (рис.1).

3. Кривая в общем случае проецируется в кривую, а прямая - в прямую. Если прямая совпадает с проецирующим лучом, например DE (рис.1), то она проецируется в точку D₁ E₁. Плоскость, проходящая через центр проекций, проецируется в прямую и называется проецирующей. Кривая, все точки которой принадлежат проецирующей плоскости, проецируется в прямую.

4. Точка пересечения линий проецируется в точку пересечения проекций этих линий (рис.1).

Центральное проецирование обладает большой наглядностью и применяется в строительном черчении, в архитектуре, в живописи и т.п. Недостатком центрального проецирования является сложность построения изображения предмета и определения истинных размеров. Поэтому оно имеет ограниченное применение в техническом черчении.

ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

Параллельное проецирование можно рассматривать как частный случай центрального проецирования с бесконечно удаленным центром проекций. Осуществляется оно пучком параллельных проецирующих лучей заданного направления. Пусть требуется построить параллельную проекцию кривой k на плоскость П₁(рис.1.2).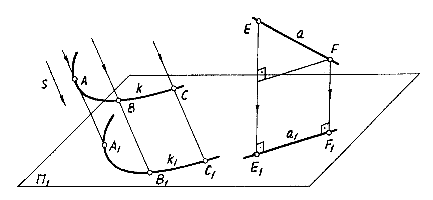

Рис. 1.2 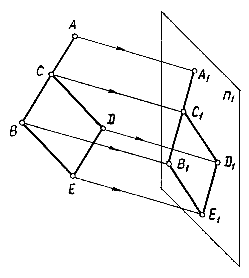Рис.1.3

Спроецируем в направлении s все точки кривой k на плоскость П₁. Чтобы спроецировать точки указанной кривой, например А, В, С, нужно провести через них прямые, параллельные направлению s, до пересечения с плоскостью П₁. Точки пересечения A₁,B₁,C₁ проецирующих лучей с плоскостью П₁ и будут параллельными проекциями точек А, В и С. Таким образом можно построить проекции множества точек кривой k. В зависимости от направления проецирования по отношению к плоскости проекций П₁ различают два вида параллельных проекций: косоугольную, когда проецирующие лучи не перпендикулярны к плоскости П₁ (рис. 1.2, кривая k), и прямоугольную (или ортогональную), когда проецирующие лучи перпендикулярны к плоскости проекций (рис.1.2, прямая а). Несмотря на то, что параллельное проецирование по сравнению с центральным дает меньшую наглядность, параллельные проекции, особенно ортогональные, обладают удобоизмеримостью и простотой построения. Поэтому ортогональное проецирование широко распространено в технике и является основным методом начертательной геометрии.

Комплексный чертеж точки

Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д

Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.

Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П₁. Проекции элементов

Рис. 60

Рис. 61

пространства на ней будем обозначать с индексом 1 : А₁, а₁, S₁ ... и называть горизонтальными проекциями (точки, прямой, плоскости).

Вторую плоскость расположим вертикально перед наблюдателем, перпендикулярно первой, назовем еевертикальной плоскостью проекций и обозначим П₂. Проекции элементов пространства на ней будем обозначать с индексом 2: А₂, <a₂, S₂ и называть фронтальными проекциями (точки, прямой, плоскости). Линию пересечения плоскостей проекций назовем осью проекций.

Спроецируем точку А ортогонально на обе плоскости проекций:

АА₁_|_ П₁;AА₁ ^П₁=A₁;

АА₂_|_ П₂;AА₂ ^П₂=A₂;

Проецирующие лучи АА₁ и АА₂ взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА₁АА₂, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.

Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П₁ с фронтальной плоскостью П₂ вращением вокруг оси П₂/П₁ (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П₂/П₁. Прямая А₁А₂, соединяющая горизонтальную А₁ и фронтальную А₂проекции точки, называется вертикальной линией связи.

Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.

Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА₁ =h) и глубиной f(AA₂ =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А₂ чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f. Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.

Комплексный чертеж прямой.

Учитывая то, что прямую линию в пространстве можно определить положением двух ее точек, для построения ее на чертеже достаточно выполнить комплексный чертеж этих двух точек, а затем соединить одноименные проекции точек прямыми линиями. При этом получаем соответственно горизонтальную и фронтальную проекции прямой.

Профильную проекцию прямой можно построить с помощью профильных проекций точек А и В. Кроме того, профильную проекцию прямой можно построить, используя разность расстояний двух ее точек до фронтальной плоскости проекций, т. е. разность глубин точек (рис. 69, в). В этом случае отпадает необходимость наносить оси проекций на чертеж. Этот способ, как более точный, и используется в практике выполнения технических чертежей.

Главные линии плоскости.

Главные линии плоскости — прямые уровня и линии наибольшего наклона плоскости к плоскостям проекций.

Линии уровня плоскости — прямые, параллельные плоскостям проекций и лежащие в данной плоскости (горизонтали, фронтали, профильные прямые плоскости).

Горизонтали плоскости — прямые, лежащие в плоскости и параллельные горизонтальной плоскости проекций.

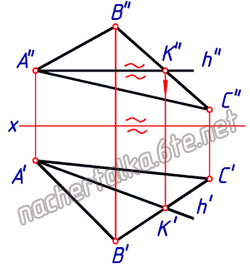
Свойства горизонтали:

— горизонтальная проекция горизонтали параллельна горизонтальной проекции горизонтального следа плоскости;

— фронтальная проекция горизонтали параллельна оси проекций.

Фронтали плоскости — прямые, лежащие в плоскости и параллельные фронтальной плоскости проекций.

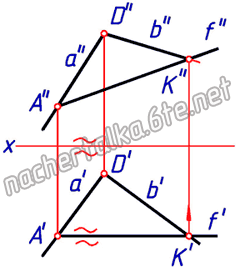
Свойства фронтали:

— фронтальная проекция фронтали параллельна фронтальной проекции фронтального следа плоскости;

— горизонтальная проекция фронтали параллельна оси проекций.

Профильные прямые плоскости — прямые, лежащие в плоскости и параллельные профильной плоскости проекций.

Линии наибольшего наклона плоскости к плоскостям проекций — прямые, лежащие в данной плоскости и перпендикулярные или к горизонталям плоскости, или к её фронталям, или к её профильным прямым. В первом случае определяется угол наклона плоскости к плоскости π1, во втором — к плоскости π2, в третьем — к плоскости π3. Линия наибольшего наклона плоскости к плоскости π1 называется линией ската плоскости.

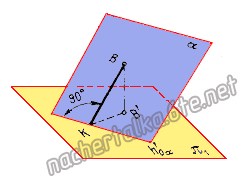
BK — линия ската плоскости α.

Свойства принадлежности.

Основные свойства принадлежности точек и прямых

1 . Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

2 . Через любые две точки можно провести прямую, и только одну.

Основные свойства взаимного расположения точек на прямой и на плоскости

1 Из трех точек на прямой одна и только одна лежит между двумя другими.

2 . Прямая разбивает плоскость на две полуплоскости.

принадлежность прямой плоскости

Сформулируем условие принадлежности прямой плоскости как аксиомы:

Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.

Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.

Проиллюстрируем примерами использование этих аксиом.

Задача. Дана плоскость (n,k) и одна проекция прямой m2 (рис.53).

Требуется найти недостающие проекции прямой m, если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.

Проекция прямой m2 пересекает проекции прямых n2 и k2 в точках В2 и С2 соответственно. Для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек, лежащих на прямых n и k соответственно.

Таким образом, точки В и С принадлежат плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит, согласно аксиоме 1, прямая принадлежит этой плоскости.

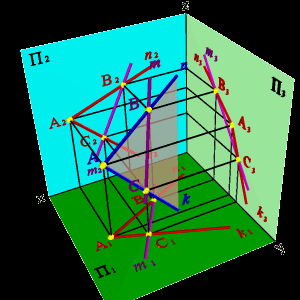
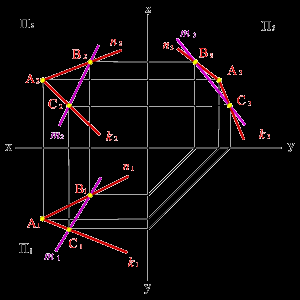
а) модель б) эпюр

Рисунок 53. Прямая и плоскость имеют две общие точки

Задача. Через точку В провести прямую m, если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k (рис.54).

Пусть точка В принадлежит прямой n, лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В2 проведем проекцию прямой m2 параллельно прямой k2, для нахождения недостающих проекций прямой необходимо построить проекцию точки В1, как точки лежащей на проекции прямой n1 и через неё провести проекцию прямой m1 параллельно проекции k1.

Таким образом, точка В принадлежит плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме 2 прямая принадлежит этой плоскости.

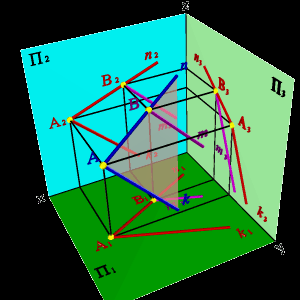
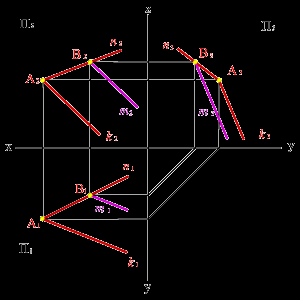
а) модель б) эпюр

Рисунок 54. Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости

10.Определение натуральной величины прямой общего положения( 2 способа)

Определение длины отрезка прямой линиии углов наклона прямой к плоскостям проекций.

Длину отрезка АВ можно определить из прямоугольного треугольника АВС |AС|=|A₁B₁|, |BС|= , угол угол наклона отрезка к плоскости П₁, угол наклона отрезка к плоскости П₂. Для этого на эпюре (рис.3.17) из точки B₁ под углом 90⁰ проводим отрезок _₁*, полученный в результате построений отрезок A₁B₁*и будет натуральной величиной отрезка АВ, а угол B₁A₁B₁* =α. Рассмотренный метод называется методом прямоугольного треугольника.

Однако все построения можно объяснить, как вращение треугольника АВСвокруг стороны AС до тех пор, пока он не станет параллелен плоскости П₁, в этом случае треугольник проецируется на плоскость проекций без искажения. Подробнее вращение вокруг оси параллельной плоскости проекций рассмотрены в разделе «Методы преобразования ортогональных проекций»

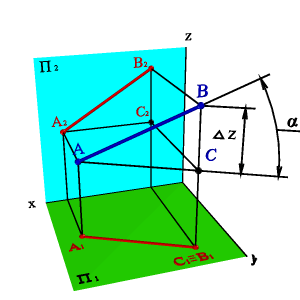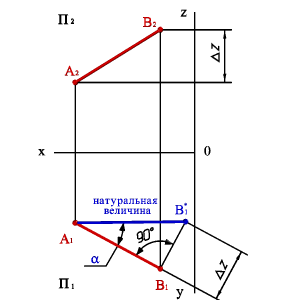а) модель	б) эпюр

Метод замены плоскостей

зменение взаимного положения изучаемого объекта и плоскостей проекций достигается путем замены одной из плоскостей П₁ или П₂ новой плоскостями П₄ (рис. 148). Новая плоскость всегда выбирается перпендикулярно оставшейся плоскости проекций.

Для решения некоторых задач может потребоваться двойная замены плоскостей проекций (рис. 149). Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

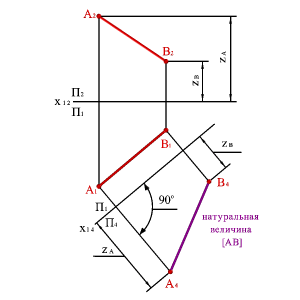
Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 148). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.

Выберем новую плоскость проекций П₄, параллельно отрезку АВ и перпендикулярно плоскости П₁. Введением новой плоскости, переходим из системы плоскостей П₁П₂ в систему П₁П₄ , причем в новой системе плоскостей проекция отрезка А₄ В₄ будет натуральной величиной отрезка АВ.

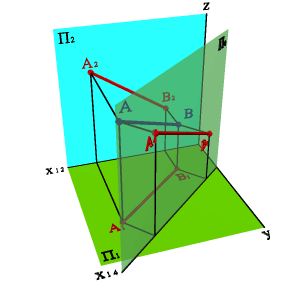а) модель	б) эпюр
Рисунок 148. Определение натуральной величины отрезка прямой методом замены плоскостей проекций

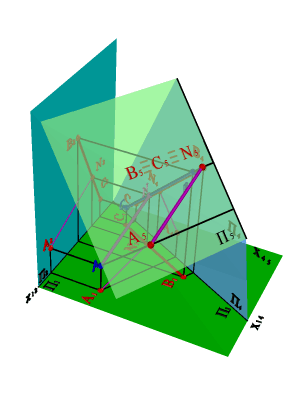
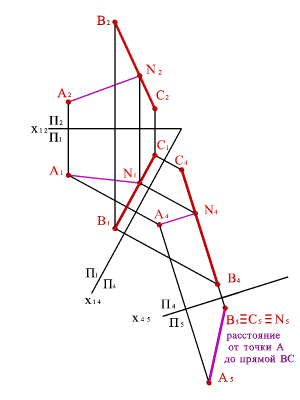
Задача 2: Определить расстояние от точки А до прямой общего положения, заданной отрезком ВС (рис._149).

Понятие многогранника.

Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Вершины и стороны многогранников являются вершинами и ребрами многогранников. Они образуют пространственную сетку. Если вершины и ребра многогранника находятся по одну сторону плоскости любой из его граней, то многогранник называют выпуклым, все его грани – выпуклые.

Из всего многообразия многогранников наибольший практический интерес представляют призмы, пирамиды, правильные многогранники и их разновидности.

Многогранник, две грани которого n-угольники в параллельных плоскостях, а остальные n-граней - параллелограммы, называется n-угольной призмой. Многогранники являются основаниями призмы, а параллелограммы – боковыми гранями призмы.

Многогранник, у которого одна из граней – произвольный многоугольник, а остальные грани – треугольники, имеющие общую вершину, называются пирамидой. Грань–многоугольник называют основанием призмы, а треугольники – боковыми гранями пирамиды. Общая вершина треугольников называется особой вершиной пирамиды (обычно, просто вершиной).

Если пирамиду отсечь плоскостью параллельной основанию, то получим усеченную пирамиду.

Многогранник называется метрически правильным, если все его грани являются правильными многоугольниками. К ним относятся куб, тетраэдр, октаэдр, икосаэдр, додекаэдр.

Под изображением многогранников на чертеже будем понимать изображение ограничивающей его многогранной поверхности, т.е. изображение совокупности составляющих ее многогранников. Графически простую многогранную поверхность удобно задавать проекциями ее сетки.

Построение проекций:

Построение проекций многогранников

Построение проекции многогранника на некоторой плоскости сводится к построению проекций точек. Например, проецируя пирамиду SABC на пл.я₂ (рис. 256, слева), мы строим проекции вершин S, А, В и С и, как следствие, проекции основания ABC, граней SAB, SBC, SAC, ребер SA, SB и др.

Также, проецируя трехгранный угол ') с вершиной S (рис. 256, справа), мы, помимо вершины S, берем на ребрах угла по одной точке (К, М, N) и проецируем их

на пл. я₂; в результате получаем проекции ребер и граней (плоских углов) трехгранного угла и В целом самый угол.

На рис. 257 изображены многогранное тело ACBB₁D... (т. е. часть пространства, ограниченного со всех сторон плоскими фигурами — многоугольниками) и его проекция на пл. я₁ — фигура A'C'F [E[DID'E'F'. Каждая точка, расположенная внутри очерка этой фигуры (т. е. линии, ограничивающей ее), является проекцией по крайней мере двух точек поверхности этого тела. Например, точка с двойным обозначением М' и N' служит проекцией точек М и N, лежащих на общей для них проецирующей прямой.

Точка, лежащая на самом очерке проекции, является проекцией или одной точки (например, А' есть проекция точки А), или нескольких, а иногда и множества точек (например, В' является проекцией не только точки В, но и множества точек грани ABC, расположенных на проецирующей прямой В В').

Проецирующие прямые, проходящие через все точки очерка проекции, в своей совокупности образуют проецирующую поверхность, внутри которой, касаясь ее, заключено данное тело. Для тела, изображенного на рис. 257, проецирующая поверхность состоит из плоскостей о^, а₂, а₃ и т. д. Линия касания проецирующей поверх-

') В данном случае выпуклый, т. е. такой, который весь расположен по одну сторону от плоскости каждой из его граней, неограниченно продолженной.

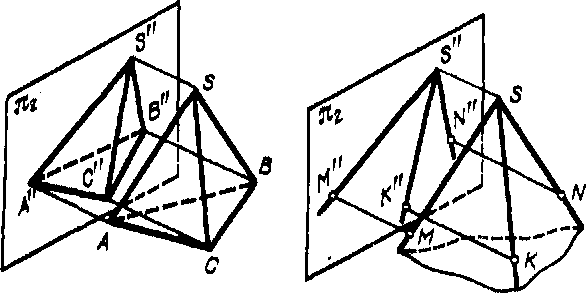
Рис. 256

Рис. 256

ности и тела называется контуром тела по отношению к выбранной плоскости проекций. На рис. 257 таким контуром служит ломаная ACF₁E₁D₁DEFA ¹).

Проецирующей поверхностью при параллельном проецировании является, как это указывалось в § 1, поверхность цилиндрическая. Если контур тела по отношению к плоскости проекций содержит прямолинейные отрезки, то проецирующая поверхность для каждого такого участка обращается в плоскую.

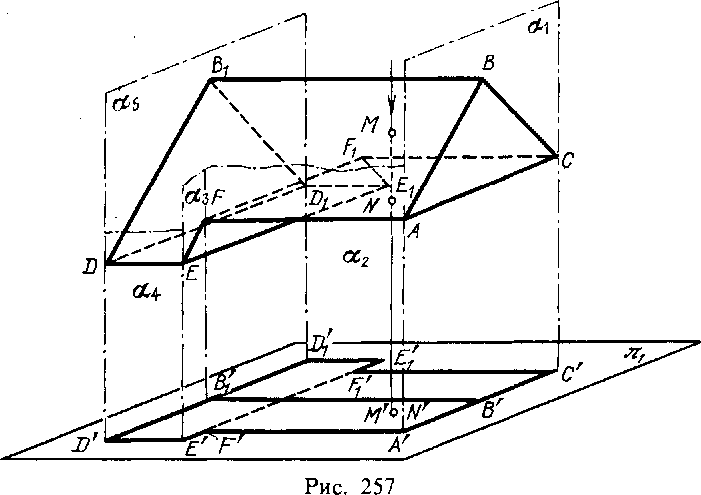
Проведенная на проекции прямая В'В{ является проекцией ребра BB_V видимого по отношению к пл. п₁. Показ на проекции тела всех видимых его ребер является обязательным.

Проекция отрезка FF₁ получается внутри очерка проекции; она показана штриховой линией, так как, по условиям видимости, точки отрезка FF_i при проецировании на пл. невидимы.

Построение проекции гранной поверхности также сводится к построению проекций некоторых точек и прямых линий этой поверхности. Проекция поверхности, ограничивающей какое-либо тело, имеет очерк, общий с очерком проекции этого тела. В случае изображения бесконечно простирающейся поверхности отделяют линиями некоторую ее часть и тем устанавливают условный контур по отношению к плоскости проекций.

Многогранник называется правильным, если его грани - правильные многоугольники, причем в каждой его вершине сходится равное число таких многоугольников.

Заметим, что число многоугольников, сходящихся в одной вершине - 3 или больше. Возьмем три пятиугольника - они действительно образуют уголок "шапочку". Три шестиугольника уже лежат в плоскости, а вот три семиугольника - не влезут. =>грани правильных многогранников не более, чем шести угольны. Т.е. правильный многогранник может быть с гранями треугольными, квадратными и пятиугольными. Причем в одной вершине может сходиться три квадрата или три пятиугольника, или три, четыре или пять треугольников.

Вариант первый. Грани многогранника - квадраты (в каждой вершине сходится три квадрата). Пусть число вершин такого многогранника - В. => число граней 3В/4. Заметим, что в каждой вершине ребер сходится столько же, сколько и граней. Число ребер такого многогранника 3В/2. Мы знаем, что В+Г-Р=2. Составим уравнение: В+3/4 В-3/2 В=2. В=8. Т.е. у такого многогранника 8 вершин, 6 граней и 12 ребер. Т.е. это куб.

Вариант второй. Грани многогранника правильные пятиугольники (в каждой вершине сходится по три пятиугольника). Г=3В/5. Р=3В/2. В+Г-Р=2. В=20. Г=12. Р=30. Это додекаэдр.

Вариант третий. Треугольники, по три. Г=3В/3=В. Р=3В/2. =>В=4=Г, Р=6. Это тетраэдр.

Вариант четвертый. Треугольники, по четыре. Г=4В/3, Р=4В/2=2В. => В=6, Г=8, Р=12. Это октаэдр.

Вариант пятый. Треугольники, по пять. Г=5В/3, Р=5В/2 => В=12, Г=20, Р=30. Это икосаэдр.

Других правильных многогранников нет.

Поверхности.

КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ

В зависимости от формы образующей и закона ее перемещения в пространстве поверхности можно разделить на отдельные группы, которые указаны на рис.3.4.
Линейчатые поверхности - поверхности, которые могут быть образованы с помощью