Тема 7. Пересечение поверхностей вращения плоскостью

И прямой линией

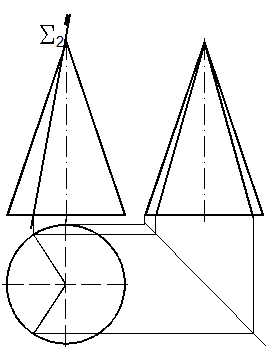
63. Построить линию пересечения конуса и фронтально проецирующей плоскости Σ (рис. 123).

63.1. Проецирующая плоскость пересекает конус через вершину и основание. Поэтому линия пересечения должна совпадать с образующей кону-са, т. е. будет в виде двух пересекаю-щихся прямых.

64. Построить линию пересечения конуса и фронтально проецирующей плоскости Σ (рис. 124).

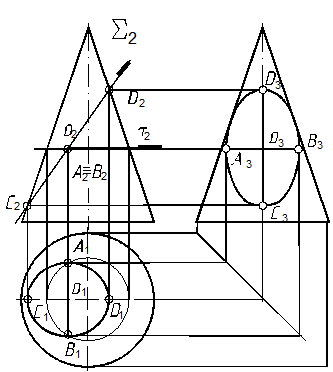64.1. Угол между секущей плоскостью и осью конической поверхности больше угла наклона образующей конической поверх-ности к его оси (рис. 124), поэ-тому в сечении получим замкну-тую линию – эллипс[72]. Определим проекции его осей.

64.2. Большая ось эллипса на П₂ проецируется в натуральную величину. Ее проекции высшей точки – D₂ и низшей – С₂. Ее горизонтальную проекцию опре-деляем по линиям связи (п. 1.3). Профильные проекции строим по правилу построения третьей проекции точки по двум известным (см. задачу 7).

Рис. 124

64.3. Малая ось эллипса на П₂ проецируется в точку, расположенную на середине отрезка между высшей и низшей точками. Через середину эллипса (точки А₂ºВ₂ проводим проецирующую плоскость t перпендикулярно оси конусной поверхности. Так как точки вращаются вокруг оси, то их траектории будут окружности (параллели) и линия пересечения плоскости, перпендикулярной к оси вращенияt любого тела, будет окружность[71], которую показываем на П₁ (тонкая линия с центром, совпадающим с проекцией оси конуса). Проводим линию связи (п. 1.3) для точек проекций центра симметрии эллипса О₁—О₂ и О₂—О₃ и определяем горизонтальную проекцию малой оси (точки А₁ и В₁ – пересечение линий связи, О₁—О₂ и окружности) Определяем ее профильную проекцию (см. задачу 7).

64.4. Строим эллипс известным способом.

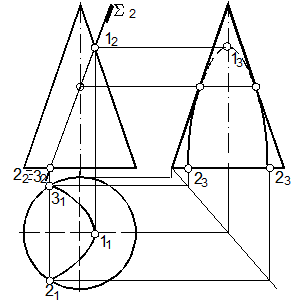65. Построить линию пересечения конуса и фронтально проецирующей плоскости Σ (рис. 125).

65.1. Секущая плоскость имеет угол наклона, одинаковый с углом наклона образующей к этой оси. Поэтому в сечении получится парабола [72], вершина которой на поверхности будет наивысшей. Находим горизонтальную проекцию линии пересечения Σ с основанием конуса ‑ 2‑3.

65.2. Определяем проекции экстремальных точек(опорные точки [73]: самая левая, правая, нижняя, верхняя, ближняя, дальняя), принадлежащих линии пересечения. По фронтальной проекции самую верхнюю (1) и нижнюю (2 и 3), самую правую (1) и левые (2 и 3) проекции точки.

65.3. По линиям связи (1.3) показываем горизонтальные проекции экстремальных точек.

65.4. По известным двум проекциям точек строим третью.

65.5. Используя опорные точки, строим проекции параболы на трех плоскостях проекций, известными способами.

66. Построить линию пересечения конуса и фронтально проецирующей плоскости Σ (рис. 126).

66.1. Так как угол наклона секущей плоскости к оси конической поверхности меньше угла наклона образующей конической поверхности, то плоскость Σ пересечет поверхность конуса по гиперболе [73], нижняя ветвь которой показана на чертеже, а верхняя (на чертеже не показана) будет зеркальным отображением нижней.

66.2. Построение проекций гиперболы аналогично построениям точек в задачах 65,

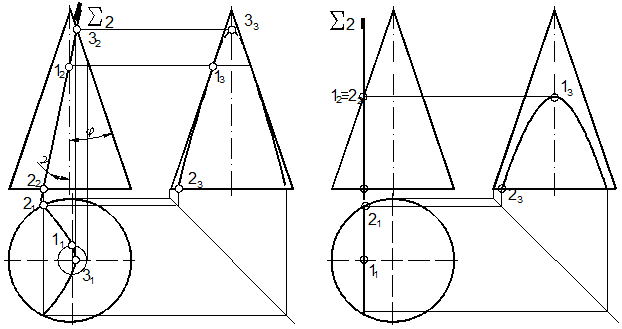
Рис. 126

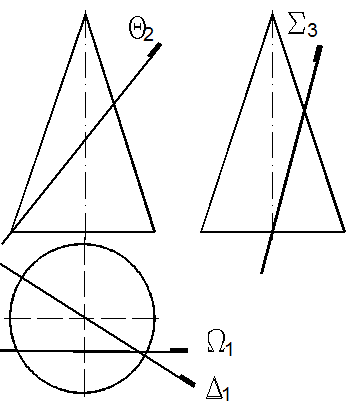
63 – 66, а. Построить недостающие проекции линии пересечения конуса и проецирующих плоскостей Σ, Q, D и W (рис. 127).

Рис. 127

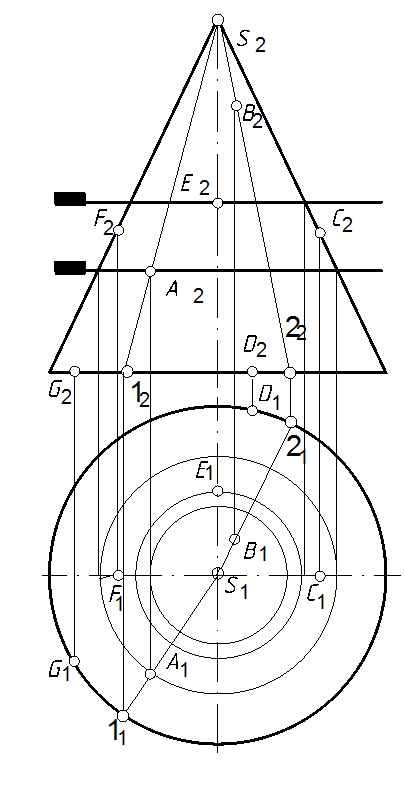
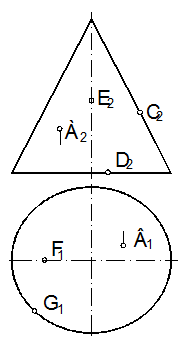
67. На конической поверхности показать два способа определения недостающих проекций точек А, В, С, D, E, F и G (рис. 128, а).

а

б

Рис. 128

67.1. Первый способ: проводим фронтально проецирующую плоскость, перпендикулярную оси вращения, через проекции точек А, Е. Линия пересечения конуса с этой плоскостью будет окружность (п. 64.3), проекцию которой показываем на горизонтальной плоскости проекций. Точка пересечения последней и линии связи будет горизонтальной проекцией точки (А, Е₂) (рис. 128, б).

67.2. Так как точка D принадлежит основанию конуса, то ее горизонтальную проекцию определим по линии связи на горизонтальной проекции основания конуса.

67.3. Фронтальная проекция точки С расположена на правой образующей, а горизонтальная – на диаметре параллельном оси Х.

67.4. Второй способ: проводим прямую, проходящую через вершину конуса проекцию точки, до пересечения с проекцией основания конуса. Находим вторую проекцию данного меридиана (линия пересечения поверхности плоскостью проходящей через ось поверхности вращения) по линиям связи (п. 1.3) определяем недостающие проекции точек.

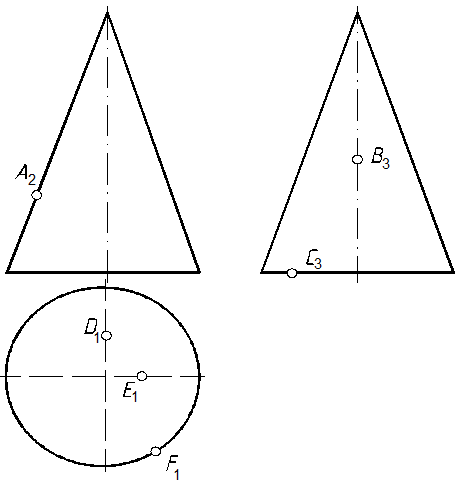67, а. На конической поверхности показать два способа определения недостающих проекций точек А, В, С, D, E, F и G (рис. 129).

Рис. 129

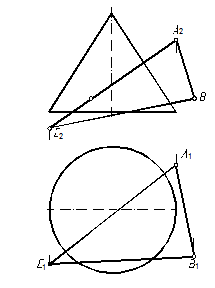68. Построить проекции линии сечения конической поверхности плоскостью Σ(ΔАВС) (рис. 130).

68.1. Чтобы упростить решение задачи, осуществим замену плоскости П₂ плоскостью П₄, перпендикулярной к П₁ (рис. 131). Дополнительную плоскость проекций выбираем таким образом, чтобы по отношению к ней секущая плоскость Σ заняла проецирующее положение (см. задачу 51, 56)

Рис. 130

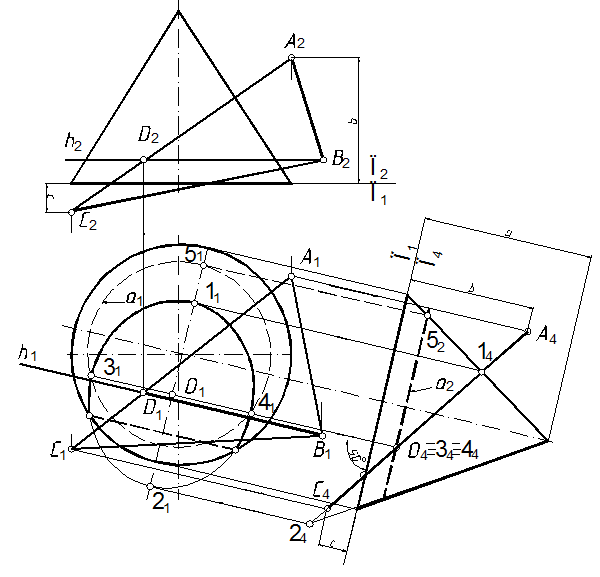Рис. 131

68.2. Спроецируем на плоскость П₄ коническую поверхность и плоскость Σ(ΔАВС). Выполненные преобразования позволили свести решение задачи к случаю, рассмотренному ранее (см. зад. 64). Линией пересечения конуса и плоскости является эллипс. Большая ось которого 12, а малая 34. На плоскости проекции П₄ – 1₄2₄ и 3₄4₄ соответственно. Определяем проекции осей эллипса на горизонтальную плоскость проекций – 1₁2₁ и 3₁4₁ (см. зад. 64). По известным проекциям малой и большой чертим эллипс известным способом.

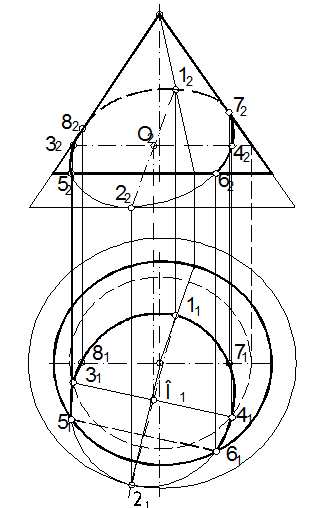68.3. Используя проекции на плоскость П₁ определяем фронтальную проекцию линии пересечения (рис. 132). Для построения фронтальной проекции сечения определяем опорные точки: 5 и 6 – нижние точки, лежащие на основании конуса; 1 и 2 – крайние точки большой оси эллипса (точка 1 принадлежит действительной линии сечения, точка 2 к обрезанной, плоскостью основания конуса, части эллипса). Кроме этих точек, определяем точки границы видимости фронтальной проекции линии, которые расположены на левой и правой образующей конуса – 7 и 8. Точки 5 и 6 – крайние точки малой оси эллипса.

Рис. 132

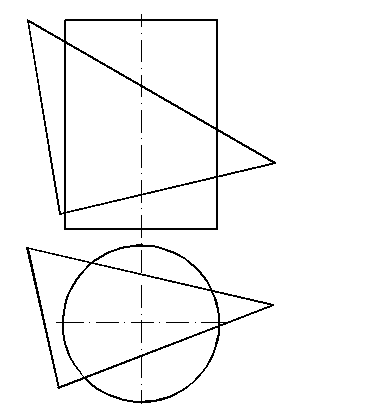68, а. Построить линию пересечения цилиндра и плоскости (рис. 133).

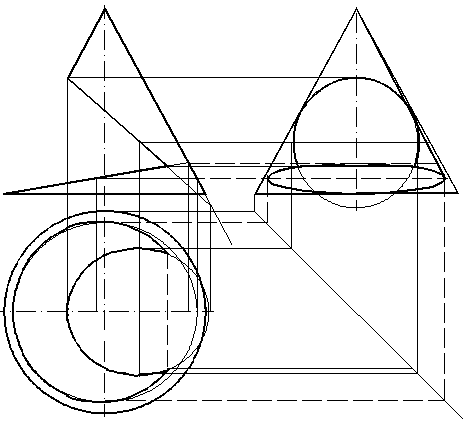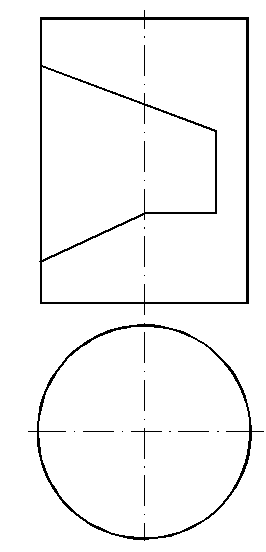
69. Построить горизонтальную и профильную проекции конической поверхности с вырезом (рис. 134).

Рис. 134

69.1. Необходимо построить линию пересечения конической поверхности с двумя фронтально проецирующими плоскостями, т. е. задача сводится к одной из задач, рассмотренных ранее (62–65).

69.2. Определяем проекции линии пересечения двух проецирующих плоскостей (63) (рис. 134).

69.3. Выделяем проекции линии принадлежащие конусу.

69.4. Строим профильную проекцию конуса с вырезом и показываем видимость линии выреза.

69, а. Построить горизонтальную и профильную проекции цилиндрической поверхности с вырезом (рис. 135).

Рис. 135

70. Построить горизонтальную и профильную проекции поверхности вращения с призматическим отверстием (рис. 136).

70. 1. Для наклонных граней отверстия (рис. 136)строим гиперболу (см. зад. 65), оставляя те части ее, которые ограничены фронтально проецирующими прямыми (см. зад. 20).

70.2. Для горизонтальной плоскости уровня получаем окружность (63.3).

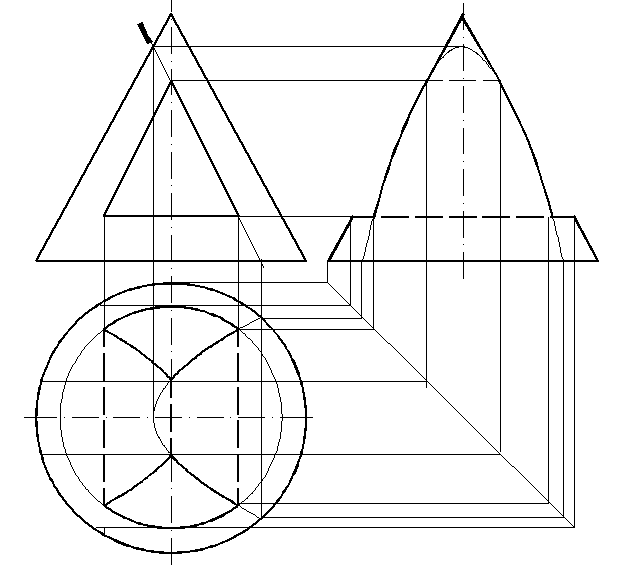
70.3. Строим профильную проекцию (см. задачу 7).

Рис. 136

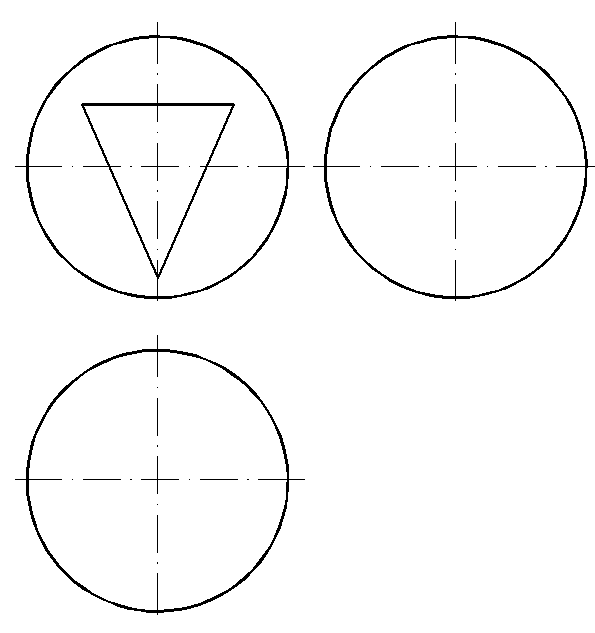70, а. Построить линию пересечения сферы с призматическим отверстием (рис. 137).

Рис. 137

Контрольные вопросы

1. Перечислить и показать возможные случаи пересечения конической поверхности и плоскости.

2. Что такое меридиан и параллель? Показать на примере.

3. Что такое опорные (экстремальные) точки)?