Способом замены плоскостей проекций

50. Преобразовать чертеж таким образом, чтобы отрезок АВ стал проецирующим (рис. 96, а).

50.1. Показываем (рис. 96, б) линию пересечения плоскости П₁ и дополнительной плоскости проекций П₄, расположенной перпендикулярно к первой плоскости проекции (способ замены плоскостей проекций).

Отрезок АВ по отношению к новой плоскости будет прямой уровня (см. задачу 10 – 12). Определим проекцию отрезка на дополнительную плоскость [53]. Для этого покажем линию пересечения плоскостей проекций П₁/П₂ и П₁/П₄ (базы отсчета[53]). Перпендикулярно этим линиям будут располагаться линии связи и проекция оси Z на плоскость П₂ и П₄. Вдоль линии связи (п. 1.3) А₁–А₄ и В₁–В₄ откладываем координаты Z_А и Z_В, измеренные на плоскости проекций П₂. Находим проекцию отрезка на эту плоскость.

50.2. Проводим плоскость П₅таким образом, чтобы по отношению к отрезку она была перпендикулярна, т. е. линии связи проекций точек отрезка на плоскость П₄ и П₅ должны быть перпендикулярна линии пересечения плоскостей проекций П₄ и П₅.

50.3. Находим проекцию отрезка на эту плоскость. От базы П₄/П₅ вдоль линии связи А₄‑А₅ откладываем значение расстояния от точки А или В до плоскости П₄ (на рис. 96, б – b).

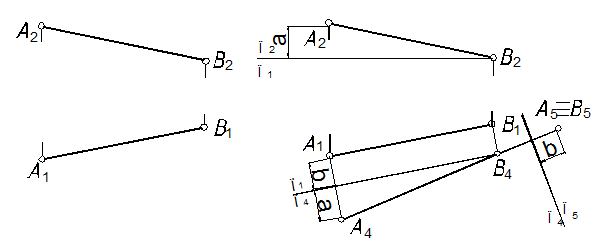а б

Рис. 96

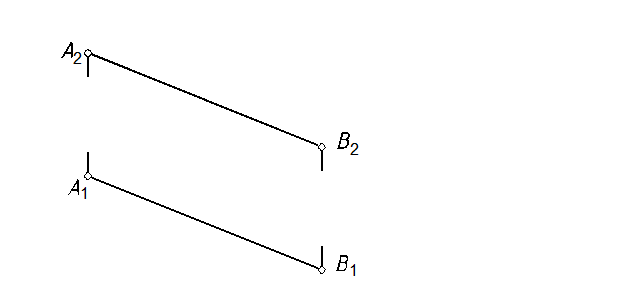50, а. Преобразовать чертеж (рис. 97)таким образом, чтобы отрезок АВ стал проецирующим. Дополнительную плоскость проекций показать перпендикулярно фронтальной плоскости проекций.

Рис. 97

51. Заменой плоскостей проекций треугольник АВС (рис. 98, а) сделать проецирующим (см. задачи 31 – 33).

51.1. В том случае, когда любая прямая, принадлежащая плоскости DАВС, будет перпендикулярна плоскости проекции, треугольник будет проецирующим на эту плоскость. Строим горизонталь h (зад. № 10), перпендикулярно которой показываем линию пересечения плоскости проекций и плоскости П₄ (рис. 98, а).

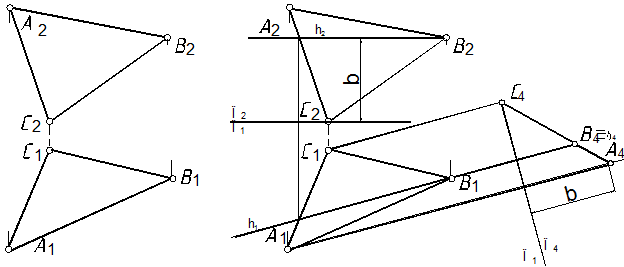51.2. Строим проекцию треугольника на плоскость П₄ (см. задачу 50).

а б

Рис. 98

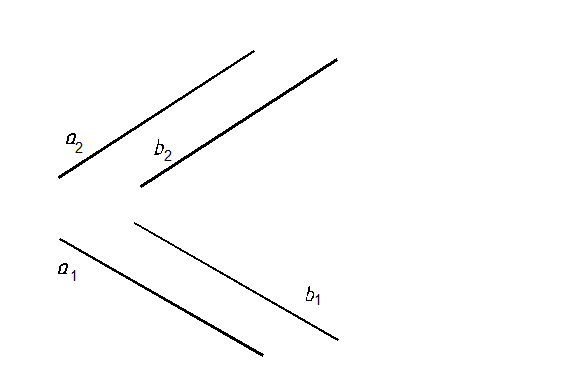51, а. Заменой плоскостей проекций сделать плоскость S(аIIb) проецирующей (рис. 99).

Рис. 99

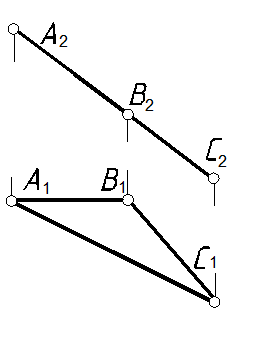52. Определить натуральную величину DАВС и центр окружности, описанной около DАВС (рис. 100).

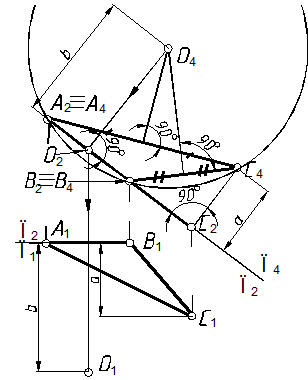
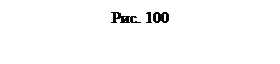52.1. Дополнительную плоскость проекций выбираем параллельно плоскости треугольника (рис. 101). На плоскость, параллельную плоскости треугольника АВС, последний будет проецироваться в натуральную величину. Дополнительную плоскость проекций П₄ проведем перпендикулярно П₂ и параллельно плоскости DАВС. Линию пересечения плоскостей П₂/П₄ показываем совпадающей с проекцией треугольника АВС, а линию пересечения горизонтальной и фронтальной плоскостей проекций (П₁/П₂) совпадающей с горизонтальной проекцией стороны АВ треугольника АВС. Определяем проекцию треугольника на плоскость П₄, которая будет являться натуральной величиной DАВС.

52.2. Центр описанной окружности лежит на пересечении перпендикуляров, восстановленных к серединам сторон треугольника.

52.3. Путем обратных преобразований находим проекции центра окружности на П₂, а затем на П₁.

Рис. 101

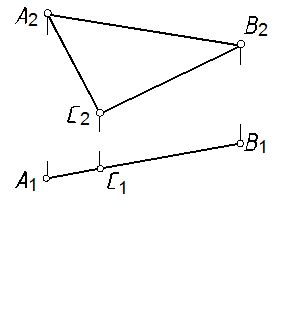52, а. Определить натуральную величину DАВС и центр окружности, описанной около DАВС (рис. 102).

Рис. 102

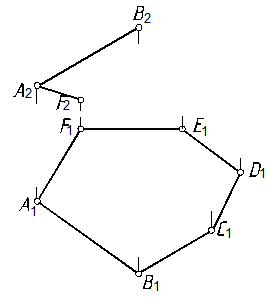53. Достроить горизонтальную проекцию многоугольника ABCDEF и определить его натуральную величину (рис. 103).

53.1. Определение горизонтальной проекции многоугольника (см. задачу 29).

53.2. При определении натуральной величины многоугольника необходимо произвести преобразование комплексного чертежа дважды. В результате первого преобразования многоугольник относи-тельно дополнительной плоскости должен быть проецирующим (см. задачу 42). Для этого необходимо плоскость П₄ провести перпендикулярно горизонтали – EF (см. зад. 10), рис. 104. Далее см. задачи 51, 52.

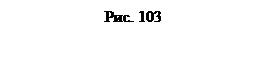
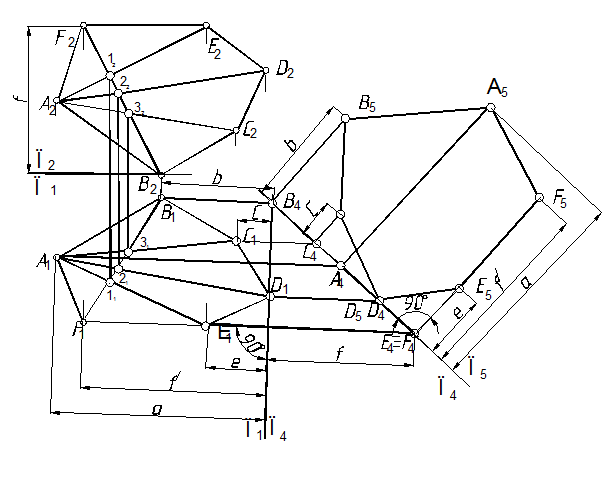
53.3. Плоскость проекции П₅ необ-ходимо провести параллельно плоскости многоугольника (плоскость уровня – задачу 34). Далее решение аналогично задачам 51, 52.

Рис. 104

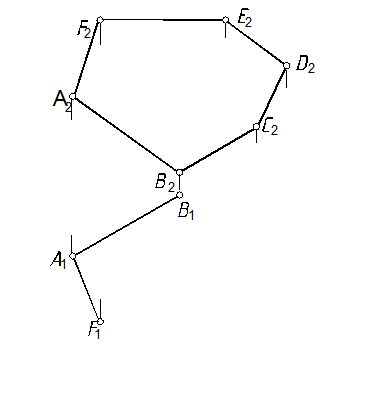
53, а. Достроить горизонтальную проекцию многоугольника ABCDEF и определить его натуральную величину (рис. 105).

Рис. 105

Контрольные вопросы

1. Цель преобразования комплексного чертежа.

2. Сущность метода замены плоскостей проекций.

3 Что такое база отсчета?

4 Какие размеры переносятся на дополнительную плоскость проекций?

Тема 6. Многогранники

54. Построить горизонтальную и профильную проекции линии пересечения пирамиды с плоскостью t (рис. 106).

54.1. Решаем способом ребер[62]:

1 показываем фронтальные проекции точек пересечения ребер с плоскостью t (см. задачу 43), рис. 106;

2 по линиям связи (п. 1.3) определяем горизонтальные и профильные проекции точек пересечения

3 соединяем соответствующие проекции точек пересечения и показываем проекции линии пересечения одновременно обозначая видидмость.

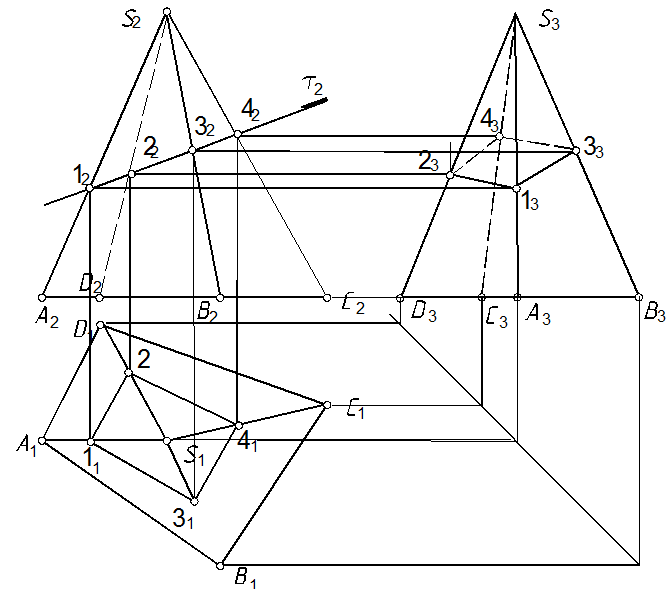
Рис. 106

Рис. 106

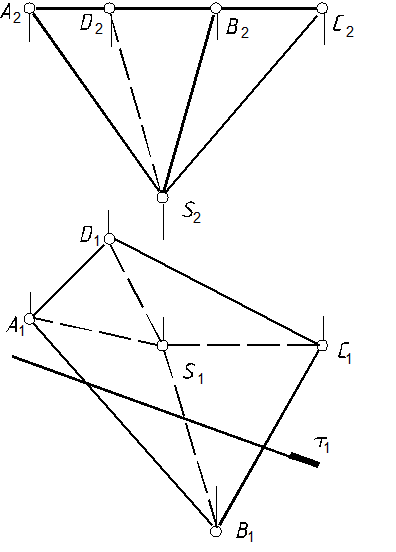54, а. Построить фронтальную и профильную проекции линии пересечения пирамиды с плоскостью t (рис. 107).

Рис. 107

55. Построить линию пересечения призмы с плоскостью S(f´h), рис. 108.

55.1. Находим точки пересечения ребер с плоскостью f´h, (см. задачу 44). В качестве проецирующих плоскостей выбираем фронтально проецирующие плоскости. Необходимо учесть, что горизонтальные проекции линий пересечения проецирующих плоскостей с плоскостью S(f´h) будут параллельны (рис. 108).

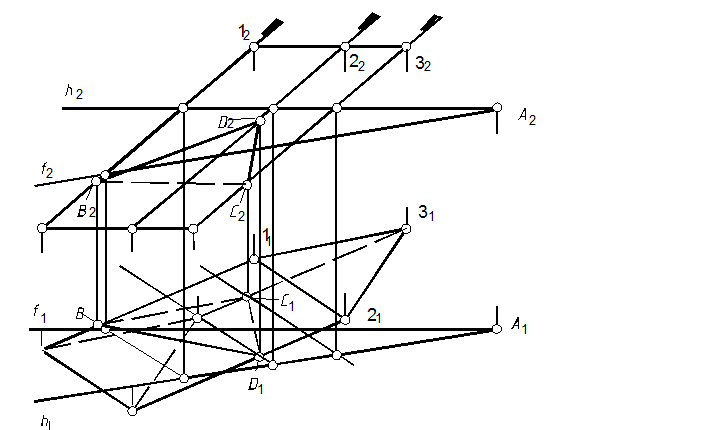Рис. 108

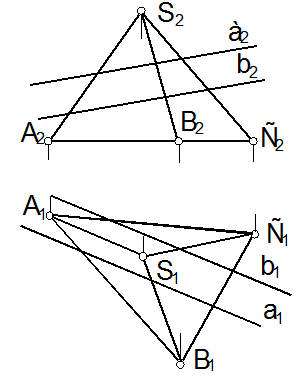55, а. Определить линию пересечения пирамиды с плоскостью общего положения W(aIIb) (рис. 109).

Рис. 109

56. Способом преобразования комплексного чертежа (гл. 5) определить линию пересечения пирамиды с плоскостью DАВС(рис. 110).

56.1. Необходимо преобразовать комплексный чертеж таким образом, чтобы плоскость DАВС стала проецирующей (см. задачу 51)

56.2. Проекции точек линии пересечения 1, 2 определяем способом ребер (рис. 112).

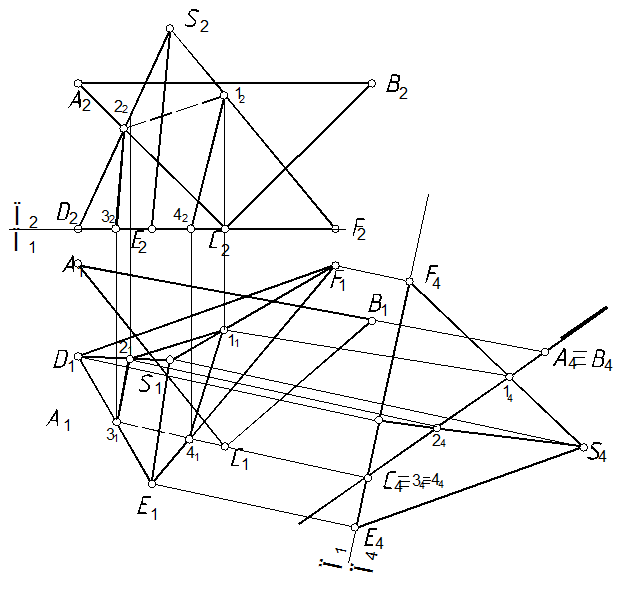
56.3. Проекции отрезка 34 точек определяем способом граней[62]: находим линию пересечения двух плоскостей – заданной D(АВС) и основания (грани) пирамиды DEF, как двух проецирующих плоскостей (см. задачу 42).

Рис. 110

56, а. Способом преобразования комплексного чертежа (гл. 5) определить линию пересечения призмы с плоскостью DАВС (рис. 111).

Рис. 111

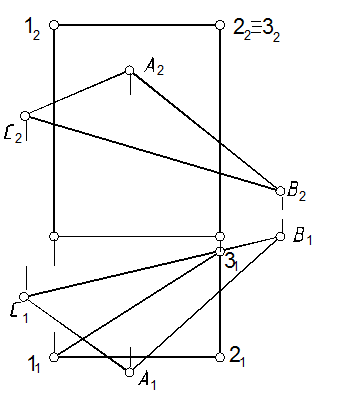
57. Определить точки встречи прямой l с многогранником и видимость участков прямой (рис. 112).

57.1. По фронтальной проекции определяем точки встречи прямой с призмой и по линиям связи (1.3) определяем горизонтальные проекции точек пересечения. Видимость определяем по конкурирующим точкам 1(2) и 3(4) (см. задачу 6 и п. 44.3).

Рис. 112

58. Определить точки встречи прямой l с пирамидой и участки видимости прямой (рис. 113, а).

58.1. Проводим фронтально проецирующую плоскость через прямую l (рис. 113, б). Определяем линию пересечения проецирующей плоскости с пирамидой (см. задачу 54). Точки пересечения прямой с этой линией будут точками пересечения прямой с многогранником.

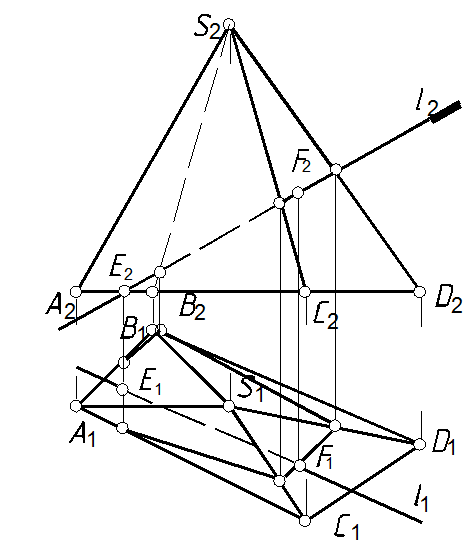
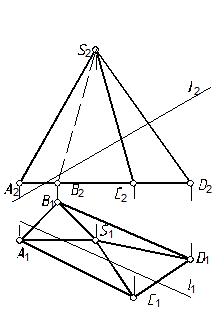
58.2. Определяем видимость прямой, см. задачи 6, 57 и п. 44.3.

а

б

Рис. 113

59. Определить точки встречи прямой линии а с многогранником и видимость участков прямой (рис. 114, а).

59.1. См. задачу 58. Определяем проекции линии пересечения (D123) призмы со вспомогательной горизонтально проецирующей плоскостью t (см. задачу 54) (рис. 114, б), на которой отмечаем проекции точек пересечения прямой с многогранником – А и В (см. задачи 55, 58).

59.2. По точкам 4(5) (см. задачи 6 и п. 44.3) определяем видимость на горизонтальной проекции, а по точкам 6(1) на фронтальной проекции.

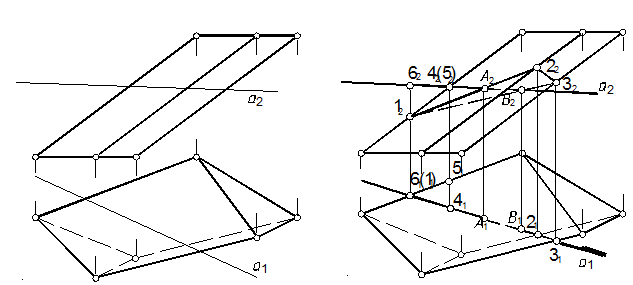
а б

Рис.114

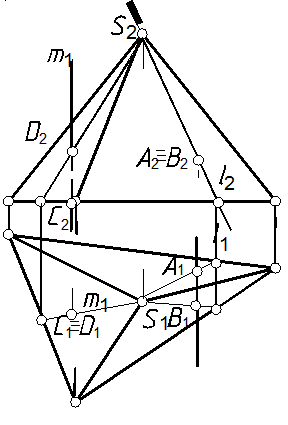60. Определить точки встречи прямой m и n с пирамидой и видимость участков прямой (рис. 115, а).

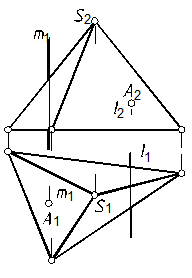60.1. Для прямой т (рис. 115, б) целесообразно на горизонтальной проекции провести проекцию прямой, прохо-дящей через проекции: вершины пирамиды, прямой т и проекцию основания пирамиды.

а б

Рис. 115

Далее показываем фронтальную проекцию этой прямой и определяем верхнюю точку пересечения. Проекция нижней точки находится на основании пирамиды.

60.2. Для прямой l (рис. 115, б) целесообразно через фронтальную проекцию вершины пирамиды провести фронтально проецирующую плоскость, пересекающую основание пирамиды и включающую прямую а. Далее см. задачу 54

59, 60, а. Определить точки встречи прямых l, n и m с призмой и их видимость (рис. 116).

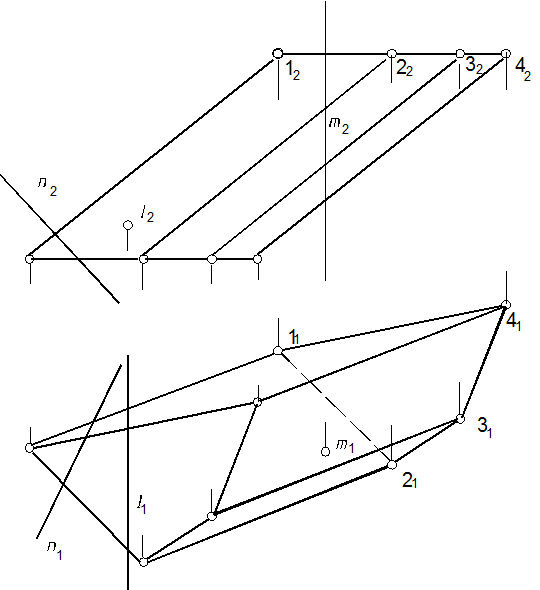Рис. 116

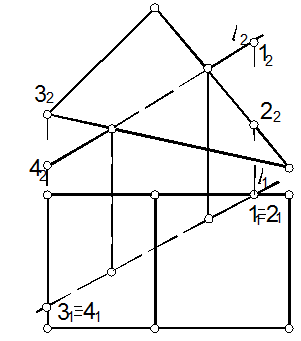
61. Построить горизонтальную и профильную проекции пирамиды с вырезом (рис. 117).

61.1. Строим профильную проекцию пирамиды (рис. 118) (см. задачу 7).

61.2. Строим линии пересечения пирамиды с двумя фронтально проецирующими плоскостями (см. зад. 42).

61.3. Определяем линии пересечения фронтально проецирующих плоскостей и показываем их на чертеже. Определяем видимость.

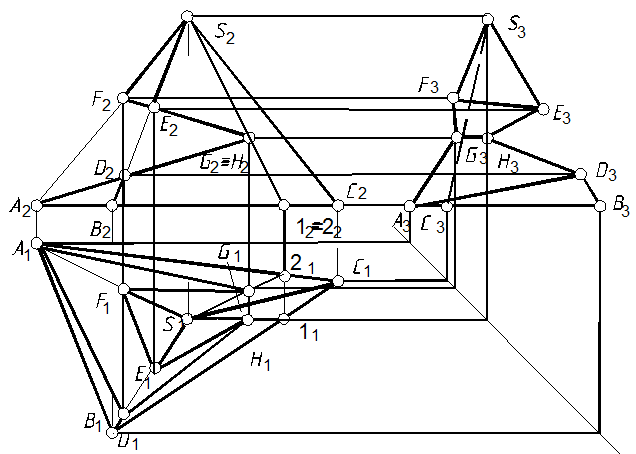
Рис. 117

Рис. 118

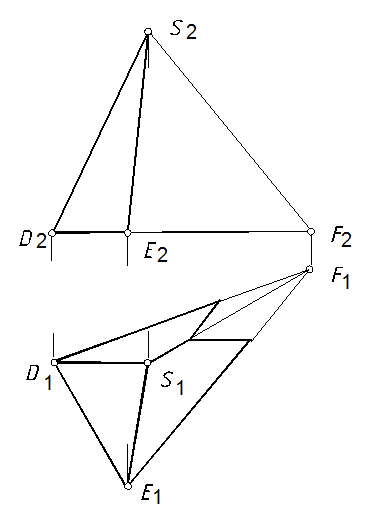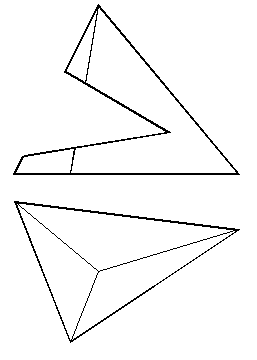
61, а. Построить горизонтальную и профильную проекции пирамиды с вырезом (рис. 119).

Рис. 119

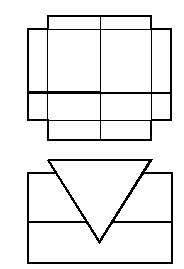62. Построить фронтальную и профильную линию пересечения призм (рис. 120).

Рис. 120

62.1. Строим (рис.121) профильную проекцию многогранников по точкам (см. задачу 7).

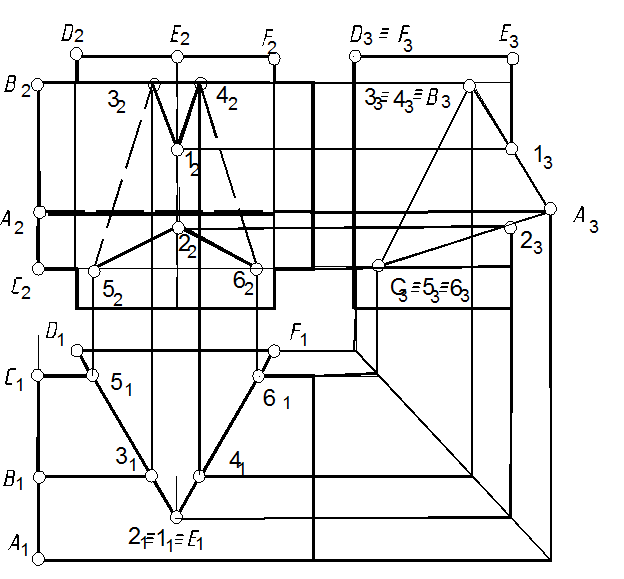
62.2. По линиям связи (п. 1.3) показываем точки пересечения проецирующих граней одной призмы с ребрами другой призмы (см. задачу 41). Соединяем их и определяем видимость линий.

Рис. 121

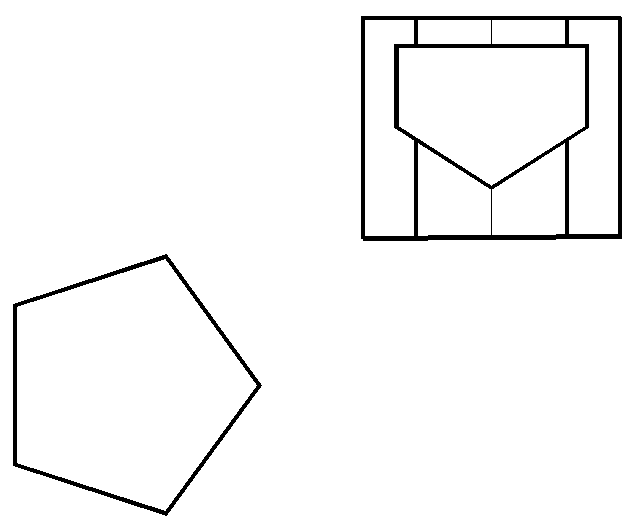
62, а. Построить фронтальную и горизонтальную проекции многогранника с призматическим вырезом (рис. 122).

Рис. 122

Контрольные вопросы

1. Что называют многогранником?

2. Как определятся линия пересечения многогранника с проецирующей плоскостью.

3. Как определяется линия пересечения многогранника с плоскостью общего положения (метод граней, метод ребер и способом замены плоскостей проекций)?

4. Как определяются точки пересечения многогранника с прямой линией?

5. Как определяется линия пересечения многогранников?