Тема 1. Комплексный чертеж точки

Тема 6. Многогранники

54. Построить горизонтальную и профильную проекции линии пересечения пирамиды с плоскостью t (рис. 106).

54.1. Решаем способом ребер[62]:

1 показываем фронтальные проекции точек пересечения ребер с плоскостью t (см. задачу 43), рис. 106;

2 по линиям связи (п. 1.3) определяем горизонтальные и профильные проекции точек пересечения

3 соединяем соответствующие проекции точек пересечения и показываем проекции линии пересечения одновременно обозначая видидмость.

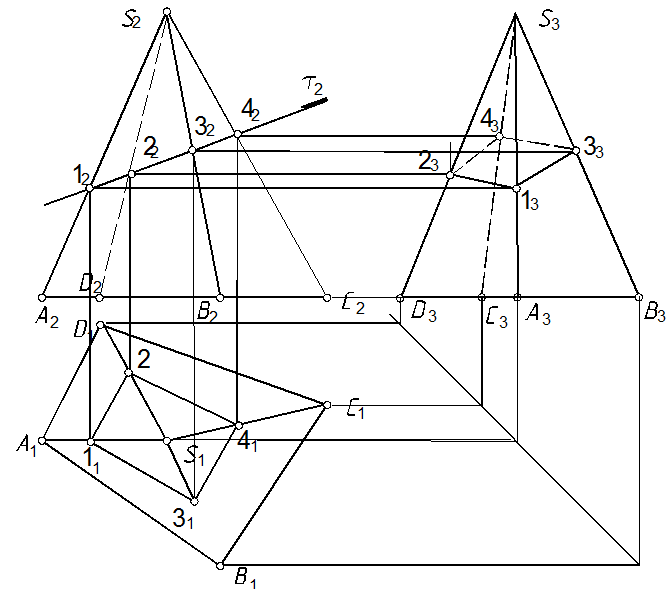
Рис. 106

Рис. 106

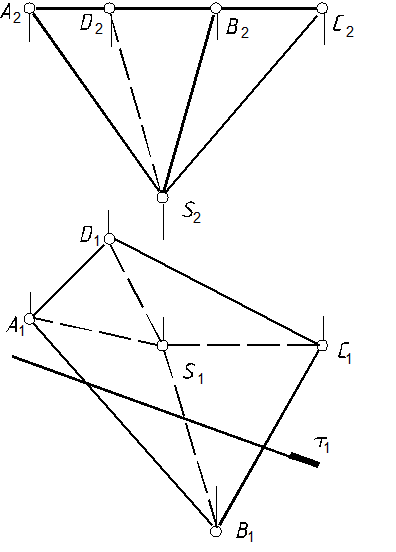54, а. Построить фронтальную и профильную проекции линии пересечения пирамиды с плоскостью t (рис. 107).

Рис. 107

55. Построить линию пересечения призмы с плоскостью S(f´h), рис. 108.

55.1. Находим точки пересечения ребер с плоскостью f´h, (см. задачу 44). В качестве проецирующих плоскостей выбираем фронтально проецирующие плоскости. Необходимо учесть, что горизонтальные проекции линий пересечения проецирующих плоскостей с плоскостью S(f´h) будут параллельны (рис. 108).

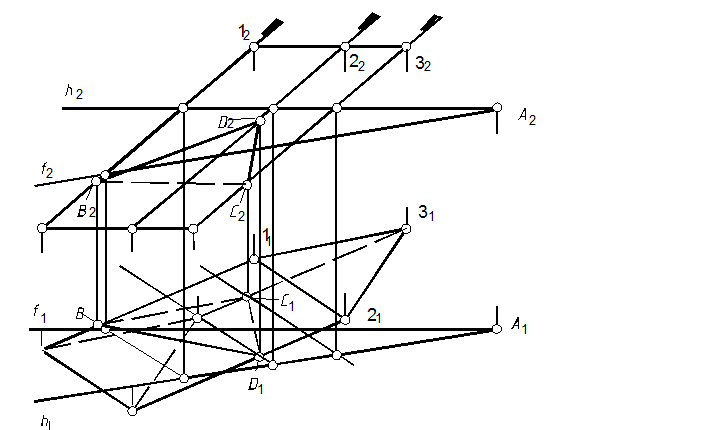Рис. 108

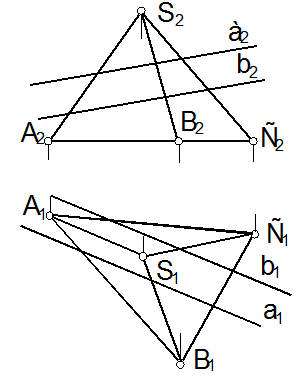55, а. Определить линию пересечения пирамиды с плоскостью общего положения W(aIIb) (рис. 109).

Рис. 109

56. Способом преобразования комплексного чертежа (гл. 5) определить линию пересечения пирамиды с плоскостью DАВС(рис. 110).

56.1. Необходимо преобразовать комплексный чертеж таким образом, чтобы плоскость DАВС стала проецирующей (см. задачу 51)

56.2. Проекции точек линии пересечения 1, 2 определяем способом ребер (рис. 112).

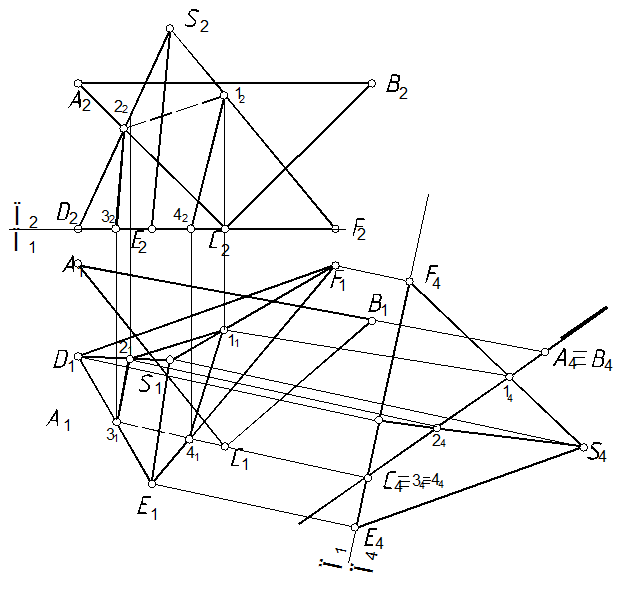
56.3. Проекции отрезка 34 точек определяем способом граней[62]: находим линию пересечения двух плоскостей – заданной D(АВС) и основания (грани) пирамиды DEF, как двух проецирующих плоскостей (см. задачу 42).

Рис. 110

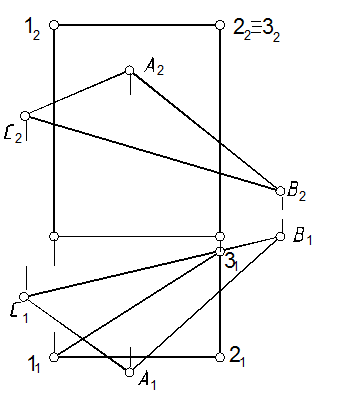56, а. Способом преобразования комплексного чертежа (гл. 5) определить линию пересечения призмы с плоскостью DАВС (рис. 111).

Рис. 111

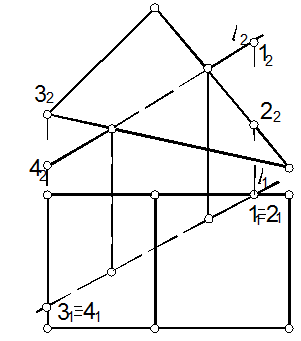57. Определить точки встречи прямой l с многогранником и видимость участков прямой (рис. 112).

57.1. По фронтальной проекции определяем точки встречи прямой с призмой и по линиям связи (1.3) определяем горизонтальные проекции точек пересечения. Видимость определяем по конкурирующим точкам 1(2) и 3(4) (см. задачу 6 и п. 44.3).

Рис. 112

58. Определить точки встречи прямой l с пирамидой и участки видимости прямой (рис. 113, а).

58.1. Проводим фронтально проецирующую плоскость через прямую l (рис. 113, б). Определяем линию пересечения проецирующей плоскости с пирамидой (см. задачу 54). Точки пересечения прямой с этой линией будут точками пересечения прямой с многогранником.

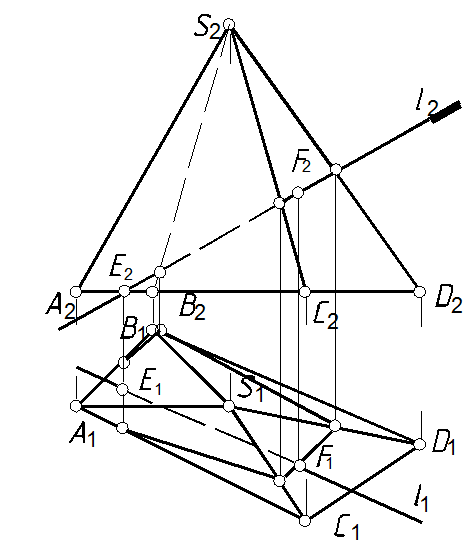
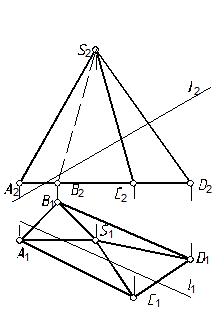
58.2. Определяем видимость прямой, см. задачи 6, 57 и п. 44.3.

а

б

Рис. 113

59. Определить точки встречи прямой линии а с многогранником и видимость участков прямой (рис. 114, а).

59.1. См. задачу 58. Определяем проекции линии пересечения (D123) призмы со вспомогательной горизонтально проецирующей плоскостью t (см. задачу 54) (рис. 114, б), на которой отмечаем проекции точек пересечения прямой с многогранником – А и В (см. задачи 55, 58).

59.2. По точкам 4(5) (см. задачи 6 и п. 44.3) определяем видимость на горизонтальной проекции, а по точкам 6(1) на фронтальной проекции.

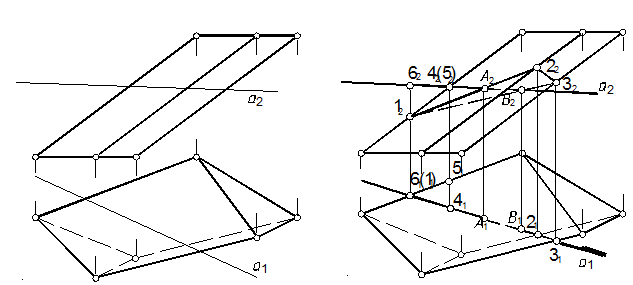
а б

Рис.114

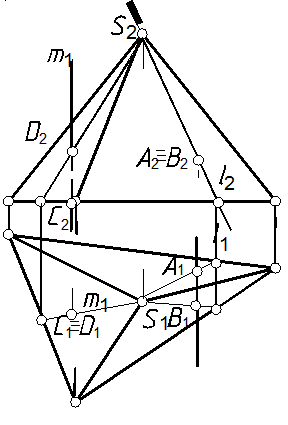60. Определить точки встречи прямой m и n с пирамидой и видимость участков прямой (рис. 115, а).

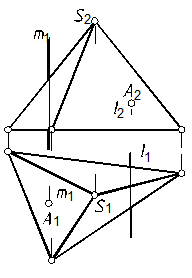60.1. Для прямой т (рис. 115, б) целесообразно на горизонтальной проекции провести проекцию прямой, прохо-дящей через проекции: вершины пирамиды, прямой т и проекцию основания пирамиды.

а б

Рис. 115

Далее показываем фронтальную проекцию этой прямой и определяем верхнюю точку пересечения. Проекция нижней точки находится на основании пирамиды.

60.2. Для прямой l (рис. 115, б) целесообразно через фронтальную проекцию вершины пирамиды провести фронтально проецирующую плоскость, пересекающую основание пирамиды и включающую прямую а. Далее см. задачу 54

59, 60, а. Определить точки встречи прямых l, n и m с призмой и их видимость (рис. 116).

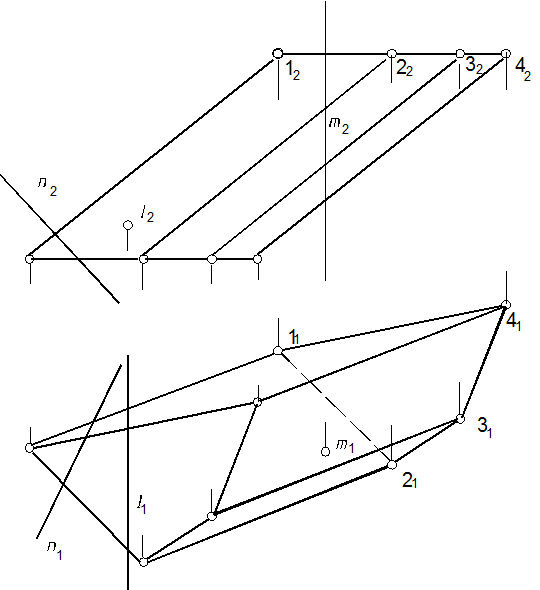Рис. 116

61. Построить горизонтальную и профильную проекции пирамиды с вырезом (рис. 117).

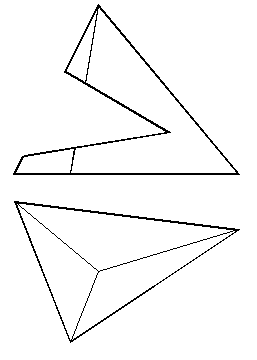61.1. Строим профильную проекцию пирамиды (рис. 118) (см. задачу 7).

61.2. Строим линии пересечения пирамиды с двумя фронтально проецирующими плоскостями (см. зад. 42).

61.3. Определяем линии пересечения фронтально проецирующих плоскостей и показываем их на чертеже. Определяем видимость.

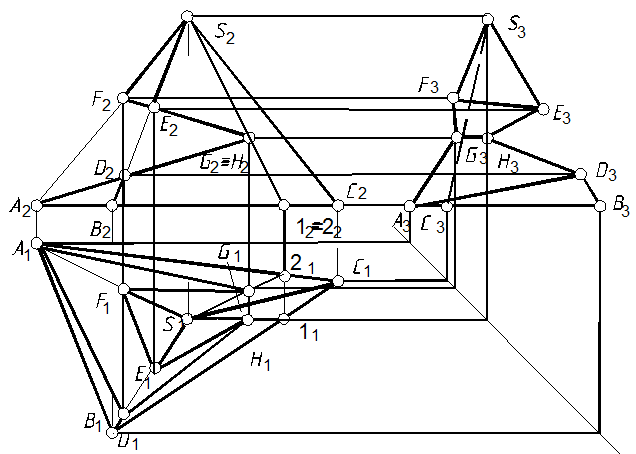
Рис. 117

Рис. 118

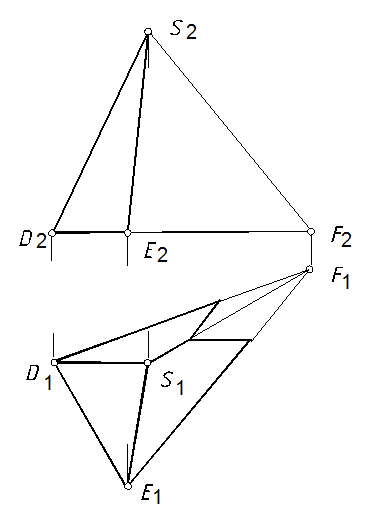61, а. Построить горизонтальную и профильную проекции пирамиды с вырезом (рис. 119).

Рис. 119

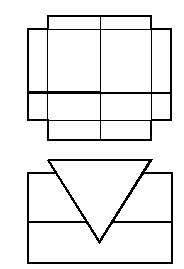62. Построить фронтальную и профильную линию пересечения призм (рис. 120).

Рис. 120

62.1. Строим (рис.121) профильную проекцию многогранников по точкам (см. задачу 7).

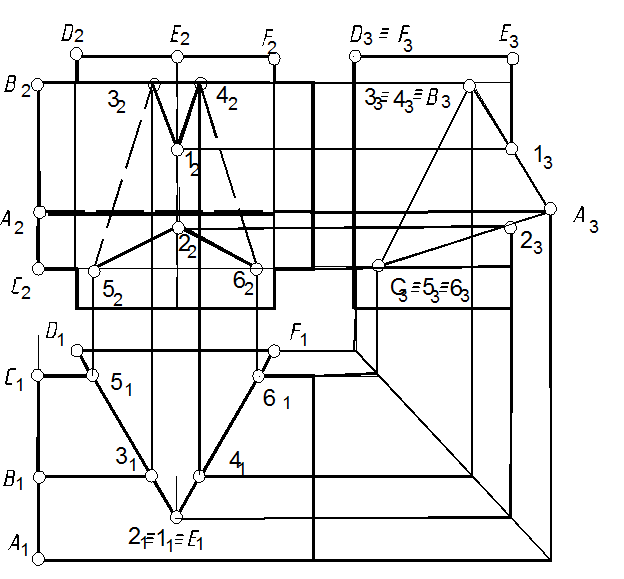
62.2. По линиям связи (п. 1.3) показываем точки пересечения проецирующих граней одной призмы с ребрами другой призмы (см. задачу 41). Соединяем их и определяем видимость линий.

Рис. 121

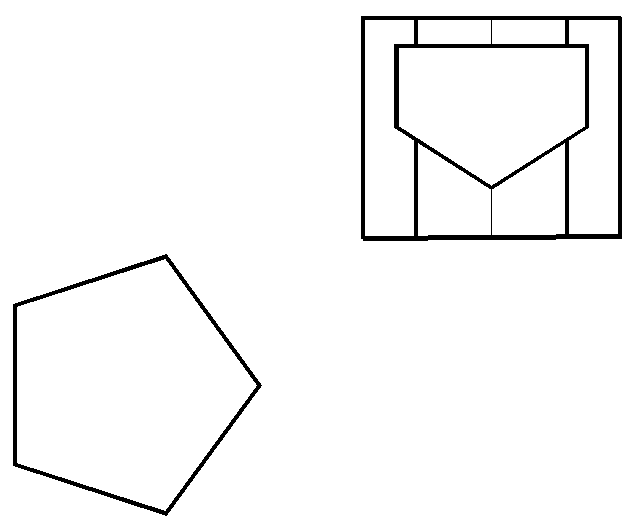
62, а. Построить фронтальную и горизонтальную проекции многогранника с призматическим вырезом (рис. 122).

Рис. 122

Контрольные вопросы

1. Что называют многогранником?

2. Как определятся линия пересечения многогранника с проецирующей плоскостью.

3. Как определяется линия пересечения многогранника с плоскостью общего положения (метод граней, метод ребер и способом замены плоскостей проекций)?

4. Как определяются точки пересечения многогранника с прямой линией?

5. Как определяется линия пересечения многогранников?

И прямой линией

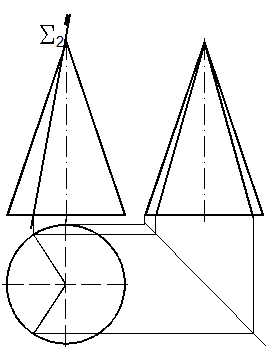
63. Построить линию пересечения конуса и фронтально проецирующей плоскости Σ (рис. 123).

63.1. Проецирующая плоскость пересекает конус через вершину и основание. Поэтому линия пересечения должна совпадать с образующей кону-са, т. е. будет в виде двух пересекаю-щихся прямых.

64. Построить линию пересечения конуса и фронтально проецирующей плоскости Σ (рис. 124).

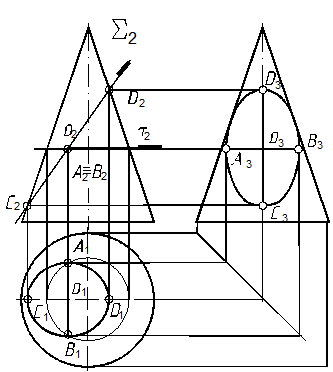64.1. Угол между секущей плоскостью и осью конической поверхности больше угла наклона образующей конической поверх-ности к его оси (рис. 124), поэ-тому в сечении получим замкну-тую линию – эллипс[72]. Определим проекции его осей.

64.2. Большая ось эллипса на П₂ проецируется в натуральную величину. Ее проекции высшей точки – D₂ и низшей – С₂. Ее горизонтальную проекцию опре-деляем по линиям связи (п. 1.3). Профильные проекции строим по правилу построения третьей проекции точки по двум известным (см. задачу 7).

Рис. 124

64.3. Малая ось эллипса на П₂ проецируется в точку, расположенную на середине отрезка между высшей и низшей точками. Через середину эллипса (точки А₂ºВ₂ проводим проецирующую плоскость t перпендикулярно оси конусной поверхности. Так как точки вращаются вокруг оси, то их траектории будут окружности (параллели) и линия пересечения плоскости, перпендикулярной к оси вращенияt любого тела, будет окружность[71], которую показываем на П₁ (тонкая линия с центром, совпадающим с проекцией оси конуса). Проводим линию связи (п. 1.3) для точек проекций центра симметрии эллипса О₁—О₂ и О₂—О₃ и определяем горизонтальную проекцию малой оси (точки А₁ и В₁ – пересечение линий связи, О₁—О₂ и окружности) Определяем ее профильную проекцию (см. задачу 7).

64.4. Строим эллипс известным способом.

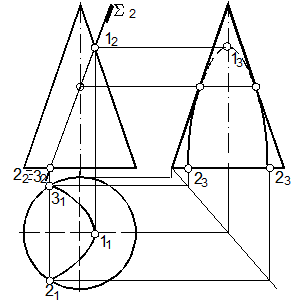65. Построить линию пересечения конуса и фронтально проецирующей плоскости Σ (рис. 125).

65.1. Секущая плоскость имеет угол наклона, одинаковый с углом наклона образующей к этой оси. Поэтому в сечении получится парабола [72], вершина которой на поверхности будет наивысшей. Находим горизонтальную проекцию линии пересечения Σ с основанием конуса ‑ 2‑3.

65.2. Определяем проекции экстремальных точек(опорные точки [73]: самая левая, правая, нижняя, верхняя, ближняя, дальняя), принадлежащих линии пересечения. По фронтальной проекции самую верхнюю (1) и нижнюю (2 и 3), самую правую (1) и левые (2 и 3) проекции точки.

65.3. По линиям связи (1.3) показываем горизонтальные проекции экстремальных точек.

65.4. По известным двум проекциям точек строим третью.

65.5. Используя опорные точки, строим проекции параболы на трех плоскостях проекций, известными способами.

66. Построить линию пересечения конуса и фронтально проецирующей плоскости Σ (рис. 126).

66.1. Так как угол наклона секущей плоскости к оси конической поверхности меньше угла наклона образующей конической поверхности, то плоскость Σ пересечет поверхность конуса по гиперболе [73], нижняя ветвь которой показана на чертеже, а верхняя (на чертеже не показана) будет зеркальным отображением нижней.

66.2. Построение проекций гиперболы аналогично построениям точек в задачах 65,

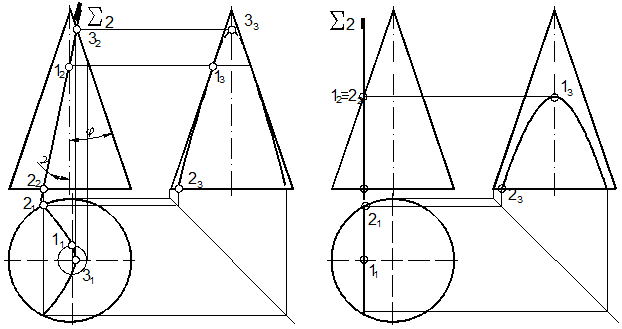
Рис. 126

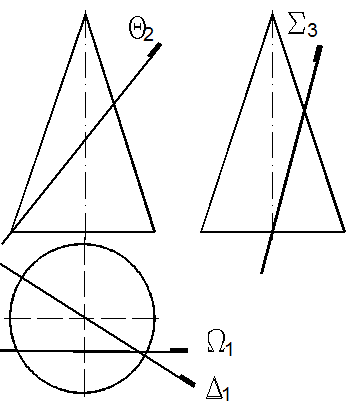
63 – 66, а. Построить недостающие проекции линии пересечения конуса и проецирующих плоскостей Σ, Q, D и W (рис. 127).

Рис. 127

67. На конической поверхности показать два способа определения недостающих проекций точек А, В, С, D, E, F и G (рис. 128, а).

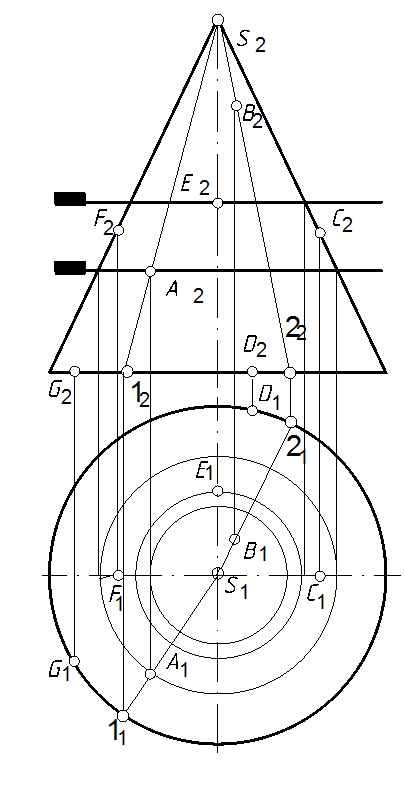
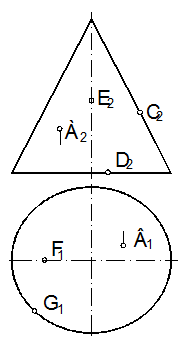
а

б

Рис. 128

67.1. Первый способ: проводим фронтально проецирующую плоскость, перпендикулярную оси вращения, через проекции точек А, Е. Линия пересечения конуса с этой плоскостью будет окружность (п. 64.3), проекцию которой показываем на горизонтальной плоскости проекций. Точка пересечения последней и линии связи будет горизонтальной проекцией точки (А, Е₂) (рис. 128, б).

67.2. Так как точка D принадлежит основанию конуса, то ее горизонтальную проекцию определим по линии связи на горизонтальной проекции основания конуса.

67.3. Фронтальная проекция точки С расположена на правой образующей, а горизонтальная – на диаметре параллельном оси Х.

67.4. Второй способ: проводим прямую, проходящую через вершину конуса проекцию точки, до пересечения с проекцией основания конуса. Находим вторую проекцию данного меридиана (линия пересечения поверхности плоскостью проходящей через ось поверхности вращения) по линиям связи (п. 1.3) определяем недостающие проекции точек.

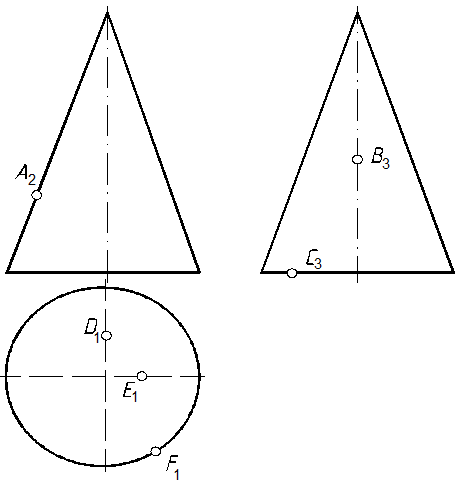67, а. На конической поверхности показать два способа определения недостающих проекций точек А, В, С, D, E, F и G (рис. 129).

Рис. 129

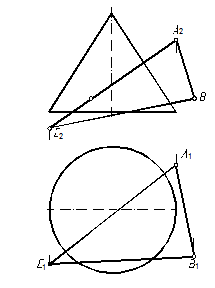68. Построить проекции линии сечения конической поверхности плоскостью Σ(ΔАВС) (рис. 130).

68.1. Чтобы упростить решение задачи, осуществим замену плоскости П₂ плоскостью П₄, перпендикулярной к П₁ (рис. 131). Дополнительную плоскость проекций выбираем таким образом, чтобы по отношению к ней секущая плоскость Σ заняла проецирующее положение (см. задачу 51, 56)

Рис. 130

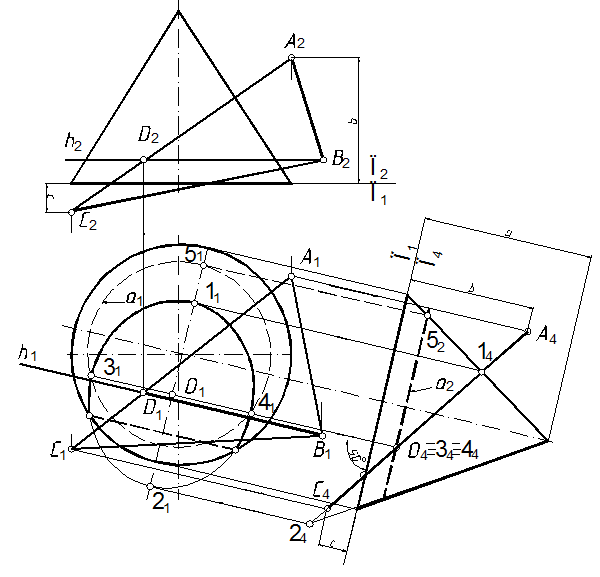Рис. 131

68.2. Спроецируем на плоскость П₄ коническую поверхность и плоскость Σ(ΔАВС). Выполненные преобразования позволили свести решение задачи к случаю, рассмотренному ранее (см. зад. 64). Линией пересечения конуса и плоскости является эллипс. Большая ось которого 12, а малая 34. На плоскости проекции П₄ – 1₄2₄ и 3₄4₄ соответственно. Определяем проекции осей эллипса на горизонтальную плоскость проекций – 1₁2₁ и 3₁4₁ (см. зад. 64). По известным проекциям малой и большой чертим эллипс известным способом.

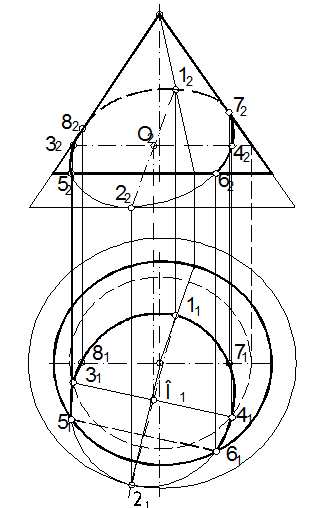68.3. Используя проекции на плоскость П₁ определяем фронтальную проекцию линии пересечения (рис. 132). Для построения фронтальной проекции сечения определяем опорные точки: 5 и 6 – нижние точки, лежащие на основании конуса; 1 и 2 – крайние точки большой оси эллипса (точка 1 принадлежит действительной линии сечения, точка 2 к обрезанной, плоскостью основания конуса, части эллипса). Кроме этих точек, определяем точки границы видимости фронтальной проекции линии, которые расположены на левой и правой образующей конуса – 7 и 8. Точки 5 и 6 – крайние точки малой оси эллипса.

Рис. 132

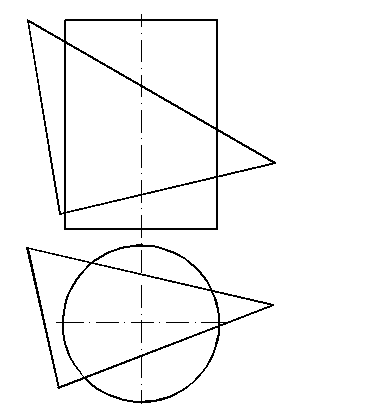68, а. Построить линию пересечения цилиндра и плоскости (рис. 133).

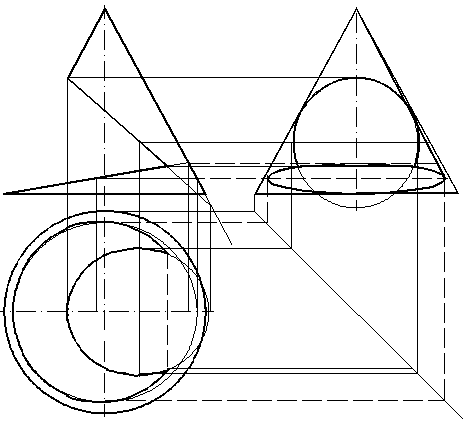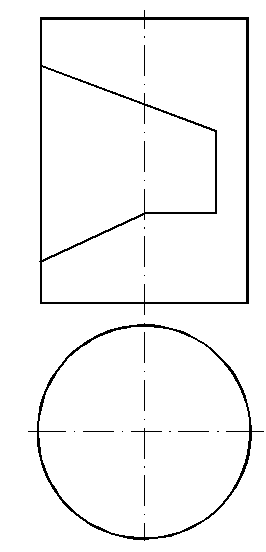
69. Построить горизонтальную и профильную проекции конической поверхности с вырезом (рис. 134).

Рис. 134

69.1. Необходимо построить линию пересечения конической поверхности с двумя фронтально проецирующими плоскостями, т. е. задача сводится к одной из задач, рассмотренных ранее (62–65).

69.2. Определяем проекции линии пересечения двух проецирующих плоскостей (63) (рис. 134).

69.3. Выделяем проекции линии принадлежащие конусу.

69.4. Строим профильную проекцию конуса с вырезом и показываем видимость линии выреза.

69, а. Построить горизонтальную и профильную проекции цилиндрической поверхности с вырезом (рис. 135).

Рис. 135

70. Построить горизонтальную и профильную проекции поверхности вращения с призматическим отверстием (рис. 136).

70. 1. Для наклонных граней отверстия (рис. 136)строим гиперболу (см. зад. 65), оставляя те части ее, которые ограничены фронтально проецирующими прямыми (см. зад. 20).

70.2. Для горизонтальной плоскости уровня получаем окружность (63.3).

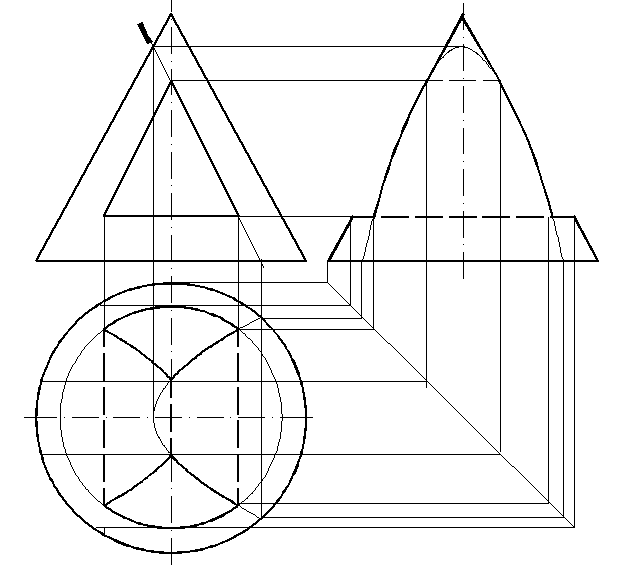
70.3. Строим профильную проекцию (см. задачу 7).

Рис. 136

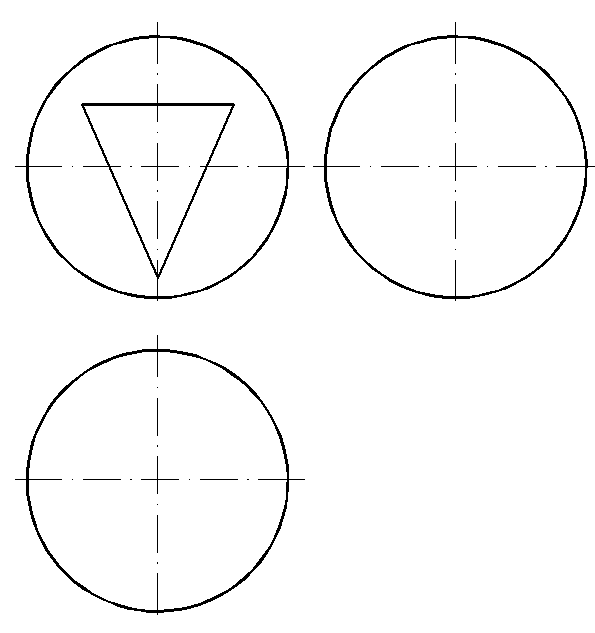70, а. Построить линию пересечения сферы с призматическим отверстием (рис. 137).

Рис. 137

Контрольные вопросы

1. Перечислить и показать возможные случаи пересечения конической поверхности и плоскости.

2. Что такое меридиан и параллель? Показать на примере.

3. Что такое опорные (экстремальные) точки)?

Библиографический список

Дергач, В. В. Лекции по начертательной геометрии: учеб. пособие / В. В. Дергач, А. К. Толстихин, И. Г. Корнева. Красноярск: ИПЦ СФУ

Лагерь, А. И. Инженерная графика (пособие для самостоятельной работы студентов) /А. И. Лагерь. Красноярск: Изд-во Краснояр. ун-та, 1992.

Левицкий, В. С. Машиностроительное черчение: учеб. для студентов вузов / В. С. Левицкий. М.: Высш. шк., 1988. 352 с.

Бубенников, А. В. Начертательная геометрия: учеб. для втузов А. В. Бубенников. – 3-е изд., перераб. и доп. – М.: Высш. шк., 1985. – 288 с., ил.

Фролов, С. А. Начертательная геометрия: учебник для втузов С. А. Фролов. 2-е изд., перераб. и доп. М.: Машиностроение, 1983. 240 с, ил,

Оглавление

ВВЕДЕНИЕ.. 3

Тема 1. Комплексный чертеж точки. 4

Тема 2. Комплексный чертеж прямой линии. 14

Тема 3. Взаимное расположение прямых в пространстве. 31

Тема 4. Плоскость. Взаимное положение прямой и плоскости. 39

Тема 5. Преобразование комплексного чертежа способом замены плоскостей проекций 64

Тема 6. Многогранники. 71

Тема 7. Пересечение поверхностей вращения плоскостьюи прямой линией. 84

Тема 8. Построение линии пересечения поверхностей. 96

Библиографический список. 105

Тема 1. Комплексный чертеж точки

Рис. 1

Решение

1.1. Ортогональное проецирование[11]–прямоугольная система координат и проецирующие лучи перпендикулярны плоскостям проекций. На наглядном изображении (рис. 2, а) проводим линии, параллельные координатным осям, и находим проекции точек на плоскости проекций. Получаем изображение координат точки: нагоризонтальной плоскости проекцийП₁ – X и Y; фронтальной плоскости проекцийП₂ – Х и Z; профильной плоскости проекций П₃ – Y и Z [18].

1.2. На наглядном изображении показываем координаты точек и при помощи линейки измеряем их значения. Откладываем соответствующие координаты на комплексном чертеже [19] (рис. 2, б). Показываем проекции точки на плоскостях проекций. Обозначаем их.

1.3. Проекции точки должны лежать на одной линии связи[19], соединяющей две проекции и перпендикулярной линии пересечения соответствующих плоскостей проекций (оси X, Y, Z и т. д.), рис. 1, а. По наглядному изображению точек (рис. 3) определить их координаты, показать недостающие проекции и построить комплексный чертеж в трех проекциях. Обозначить плоскости проекций и написать их название.

а б

Рис. 2

1, а. По наглядному изображению точек определить их координаты, показать третью проекцию и построить комплексный чертеж в трех проекциях (рис. 3). Обозначить плоскости проекций и написать их название.

А( ); B( ); C( ); D( ); E( ); F( );

G( ); H( )

Рис. 3

2. По комплексному чертежу задачи 1 (рис. 2) определить положение точек относительно точки А.

Решение

2.1. Точка находится правее[21], если ее координата X (см. задачу 1) меньше. Определяем по горизонтальной или фронтальной плоскости проекций – правая точка располагается правее. Таким образом для нашего случая точками находящимися правее точки А, будут: B, D; левее Е и F.

2.2. Точка находится выше[21], если ее координата Z (см. задачу 1) больше. На фронтальной и профильной плоскостях проекций точка располагается выше. Выше точки А, для задачи, точек не будут. Остальные точки расположены ниже.

2.3. Точка находится ближе [21] к наблюдателю, если ее координата Y (см. задачу 1) больше. На горизонтальной плоскости проекций находится ниже, а на профильной плоскости проекций правее, и для нашего случая: ближе точки А – точки С и D; остальные – В и Е – дальше.

2, а. При условии задачи 2 решить задачу (рис. 3).

Правее: Левее:

Выше: Ниже:

Ближе: Дальше:

3. Даны точки: А(30, 20, 10), В(40 -25, 50), С(10, 50, 0), D(0, 0, 0). Определить (по значениям координат) правую, левую, высшую, низшую, ближайшую и наиболее удаленную точки.

Решение:

Правая – D, так как ее координата Х наименьшая.

Левая – B, так как ее координата Х наибольшая.

Высшая – B, так как ее координата Х наибольшая.

Низшие – C, D, так как их координата Z наименьшая.

Ближайшая – C, так как ее координата Х наибольшая.

Наиболее удаленная – B, так как ее координата У наименьшая.

3, а. Даны точки: А(-30, 20, 10), В(40 -25, -50), С(10, -50, 0), D(0, 0, 0). Определить (по значениям координат) правую, левую, высшую, низшую, ближайшую и наиболее удаленную точки.

Правая – Высшая ‑ Ближайшая –

Левая – Низшая ‑ Наиболее удаленная –

4. По комплексному чертежу определить положение точки A относительно точки В (рис. 4, а) и С относительно D (рис. 4, б).

а б

Рис. 4

5. Построить наглядные изображения и эпюр точек задачи № 3, а и проверить правильность нахождения положения точек друг относительно друга.

Решение

5.1. Решение аналогично задачи 1. По известным координатам показываем наглядное изображение точек и строим их эпюр (рис. 5). Координата Y точки В отрицательна, поэтому (на эпюр) она совпадет с положительными координатами осей Z и X, но не будет им равна.

Рис. 5

5, а. Построить наглядные изображения и эпюр точек задачи № 3, а и проверить правильность решения (рис. 6).

Рис. 6

6. Определить видимость точек, изображенных на чертеже. Написать их названия (рис. 7).

Рис. 7

Решение

6.1. Точки, у которых одна из проекций совпадает (одинаковая координата), называются конкурирующими [23]. Плоскость, на которой проекции совпадают, определяет название этих точек (горизонтально, вертикально и профильно конкурирующие точки). На другой плоскости проекций эти точки лежат на одной линии связи.

6.2.Видимость [23] точек (рис. 8) определяем по направлению проецирования (взгляда, направленного в сторону, противоположную положительного отсчета координат (стрелка): – для горизонтально-конкурирующих точек направление проецирования сверху вниз на фронтальной и профильной плоскостях проекций, фронтально-проецирующих точек – снизу вверх на горизонтальной плоскости проекций и справа налево на профильной плоскости проекций, профильно-конкурирующих – слева направо на горизонтальной и фронтальной плоскости проекций.

6.3. При символьном обозначении видимости сначала пишется видимая точка, а затем в круглых скобках – невидимая, например А₁(В₁) – горизонтально-конкурирующие точки, из которых точка А видна. Для нашего случая имеем (рис. 8):

B(G) – фронтально-конкурирующие;

В(А) – горизонтально-конкурирующие;

H(I) – горизонтально-конкурирующие;

Е(F) – профильно-конкурирующие;

D(C) – фронтально-конкурирующие.

Рис. 8

6, а. Определить видимость точек, изображенных на чертеже (рис. 9). Написать их названия.

Рис. 9

7. По двум проекциям точки А построить третью (рис. 10, а).

Решение

7.1. Построение третьей проекции точки по двум известным[27] основано на том, что любые две проекции точки определяются тремя координатами, две из которых определяют положение какой-либо проекции. Так для нашего случая, чтобы определить положение третьей проекции (рис. 10, б), достаточно определить координату Y_A на горизонтальной проекции и отложить ее вдоль линии связи А₂–А_3.

а б)

Рис. 10

7, а. По двум проекциям точек построить третью (рис. 1.11).

7.1. Рассмотреть пару точек, имеющих одноименные проекции, для которых произвольно показать систему координат (удобнее начало координат совместить с одной из точек. Далее см. задачу 7.

Рис. 11

Контрольные вопросы

1. Ортогональное проецирование точки.

2. Основные плоскости проекций (наименование и их расположение в пространстве).

3. Проекции точки на три основные и дополнительные плоскости проекций (наглядное представление и комплексный чертеж).

4. Линии связи, их расположение по отношению к линии пересечения плоскостей проекций (координатным осям).

5. Определение по комплексному чертежу и координатам взаимного расположения точек в пространстве (правее, левее; выше, ниже; ближе, дальше).

7. Конкурирующие точки, определение видимости точек.

8. Построение третьей проекции точки по двум известным.