Укажите номера верных утверждений.

1) В любой ромб можно вписать окружность.

2) В прямоугольном треугольнике косинус одного из углов равен 0.

3) Отношение площадей подобных треугольников равно коэффициенту подобия.

Укажите в порядке возрастания номера неверных утверждений.

1) Ромб, диагонали которого равны, является квадратом.

2) Противоположные углы параллелограмма равны между собой.

3) тангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету.

4) если в треугольнике все углы равны между собой, то это – равносторонний треугольник.

5) сумма углов треугольника равна 180 градусам.

Укажите в ответе номера неверных утверждений.

1) Около любого прямоугольника можно описать окружность.

2) В любой ромб можно вписать окружность.

3) Если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб.

4) Если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник.

5) Если в трапецию можно вписать окружность, то эта трапеция – равнобедренная.

Какие из следующих утверждений верны?

1) Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

2) Середина гипотенузы прямоугольного треугольника равноудалена от всех его сторон.

3) Сумма углов выпуклого четырехугольника не превышает 360⁰ .

4) Если две стороны и три угла одного треугольника равны соответственно двум сторонам и трем углам другого треугольника, то такие треугольники равны.

5) Существует треугольник, в котором точка пересечения серединных перпендикуляров, проведенных ко всем его сторонам, лежит на одной из этих сторон.

Укажите в ответе номера неверных утверждений.

1) В любом ромбе все стороны равны.

2) Существует ромб, все стороны которого – различны.

3) В любом прямоугольнике все стороны равны.

4) Существует прямоугольник, все стороны которого – различны.

5) В любой трапеции все стороны равны.

Итоговый тест по теме: Основные теоремы и факты. Вариант 2.

1. Какие из данных утверждений верны? Запишите их номера.

1) Любой параллелограмм можно вписать в окружность.

2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти прямые параллельны.

3) Точка пересечения двух окружностей равно удалена от центров этих окружностей.

2. Какие из данных утверждений верны?

1) Сумма углов любого выпуклого шестиугольника равна 940°

2) В любой параллелограмм можно вписать окружность.

3) Существует только одна точка, равноудаленная от всех вершин данного треугольника.

4) Одна из высот прямоугольного треугольника всегда делит его на два подобных треугольника.

3. Укажите в порядке возрастания номера неверных утверждений:

1) Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

2) Соседние углы параллелограмма равны между собой.

3) Сумма углов треугольника равна 90°.

4) Параллелограмм, диагонали которого равны, является прямоугольником

5) Если в треугольнике два угла равны между собой, то это – равнобедренный треугольник.

4. Укажите в ответе номера неверных утверждений.

1) В любом прямоугольнике диагонали равны.

2) Существует прямоугольник, диагонали которого различны.

3) В любом ромбе диагонали равны.

4) Существует ромб, диагонали которого различны.

5) В любой трапеции диагонали равны.

5. Какие из следующих суждений верны?

1) если в ромбе диагонали равны, то этот ромб – квадрат.

2) Середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.

3) Сумма углов треугольника не превышает 180°.

4) Если сторона и три угла одного треугольника равны стороне и трем углам другого треугольника, то такие треугольники равны.

5) Существует треугольник, все высоты которого пересекаются в одной из его вершин.

6. Укажите в ответе номера верных утверждений.

1) В любом параллелограмме есть хотя бы один острый угол.

2) В любом параллелограмме есть хотя бы один прямой угол.

3) В любом параллелограмме есть хотя бы один тупой угол.

4) В любой трапеции есть хотя бы один острый угол.

5) В любой трапеции есть хотя бы один тупой угол.

Углы

1. В равнобедренном треугольнике угол при вершине, противолежащей основанию, равен 58⁰.Найдите угол при основании. Ответ дайте в градусах.

2. В треугольнике АВС внешний угол при вершине А равен 125 ⁰, а внешний угол при вершине В равен 59⁰.Найдите угол С. . Ответ дайте в градусах.

3. В треугольнике АВС проведена высота СН, которая делит угол С на два угла, величины которых 47⁰ и 71⁰. Найдите наименьший из двух оставшихся углов. Ответ дайте в градусах.

4. В параллелограмме АВСМ прямая АС делит угол при вершине А пополам. Найдите угол, под которым пересекаются диагонали параллелограмма. Ответ дайте в градусах.

5. Угол А равнобедренной трапеции АВСD с основаниями ВС и AD равен 53⁰. Найдите сумму углов В и С.

6. Два угла ромба относятся как 4:6. Найдите меньший угол Ответ дайте в градусах.

7. Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.

8. Найдите центральный угол АОВ, если он на 67⁰ больше вписанного угла АСВ, опирающегося на ту же дугу.

Задачи повышенного уровня

9. Сумма углов А и В вписанного четырёхугольника АВСD равна 204⁰, а сумма углов В и С равна 192⁰. Найдите угол D.

10. Докажите, что биссектрисы смежных углов перпендикулярны.

11. Докажите, что градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу.

12. Докажите, что если биссектриса пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник.

13. Биссектрисы всех внутренних углов параллелограмма попарно пересекаются. Докажите, что полученный четырёхугольник является прямоугольником.

14. Биссектриса угла В треугольника АВС делит медиану, проведённую из вершины С, в отношении 7:2, считая от вершины С. В каком отношении, считая от вершины А, эта биссектриса делит медиану, проведённую из вершины А?

Тема: Углы. Вариант 1

А

1.Какой угол (в градусах) образуют

минутная и часовая стрелки часов в 5 часов?

2. .На рисунке∠1=108°, ∠2=72°,∠5=83°. а в f

Найдите угол 4. 4

1 d

c

2 5

3. .Точка О – центр окружности ∠АОВ=84°

(см. рисунок). Найдите величину

угла AСB (в градусах) С О

А В

4. Найдите ∠ С, если ∠А=62°. В

А О С

5. Найдите величину угла АВС. Ответ дайте в градусах

В

А С

Тема: Углы. Вариант 2

1.Точка О – центр окружности∠ВОС=50° (см. рисунок). Найдите величину угла ВАС (в градусах) А В

О С

2.На плоскости даны четыре прямые (см. рисунок) 3

.Известно, что ∠1=130°, ∠2=50°,∠3=45°. 2

Найдите ∠5. Ответ дайте в градусах. 1 6 4

3. Точка О – центр окружности,

∠АСВ=25° (см. рисунок). Найдите С О

величину угла АОВ (в градусах). А В

4 Точка О – центр окружности∠ВАС=70°

(см. рисунок). Найдите величину В

угла ВОС (в градусах). А О

С

5. Найдите величину угла АВС. Ответ дайте в градусах

В В

А С

Тема: Углы Вариант 5

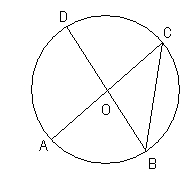
1. Величина центрального угла AOD равна 110⁰.

Найдите величину вписанного угла ACB. Ответ дайте в градусах.

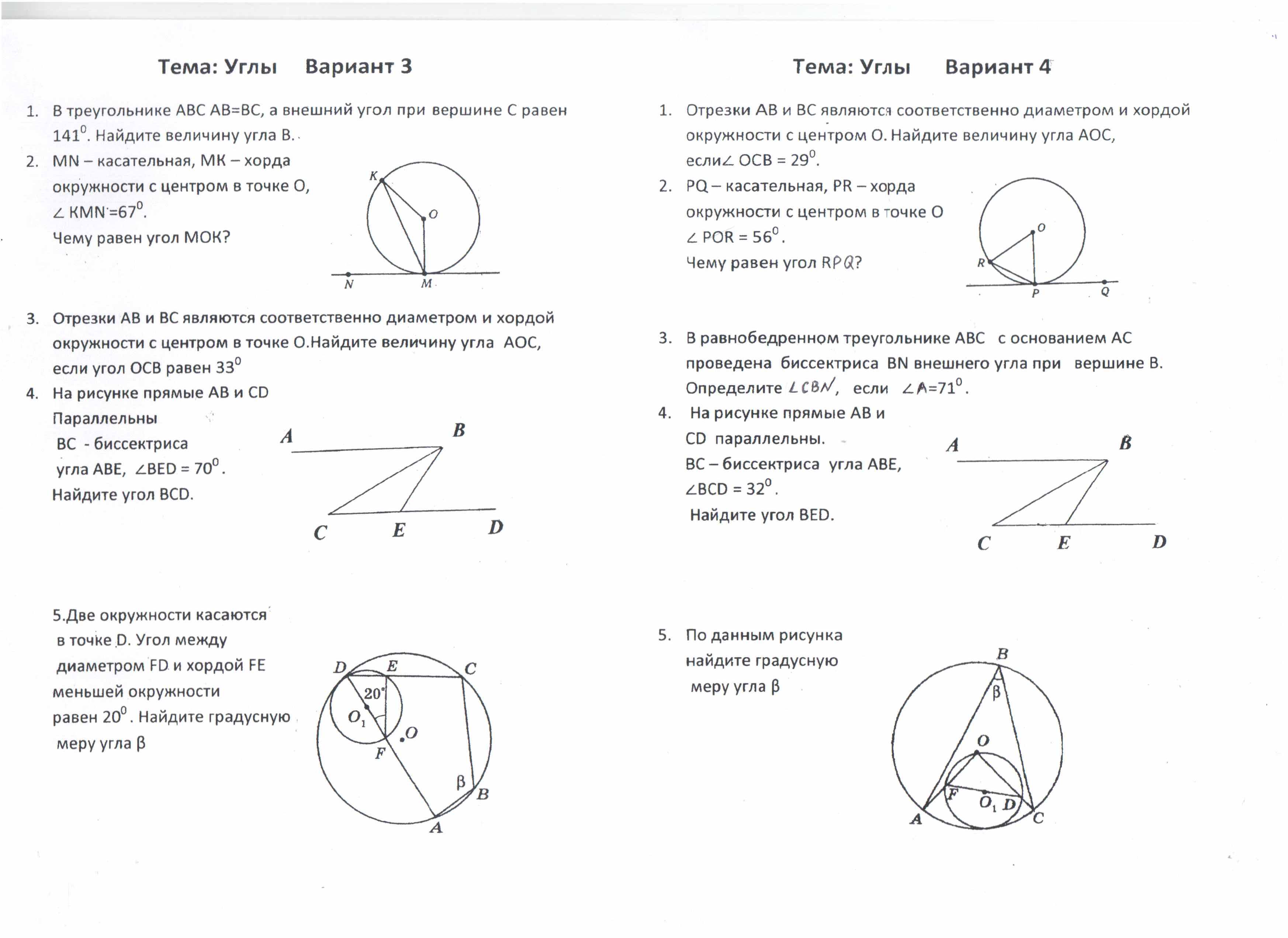
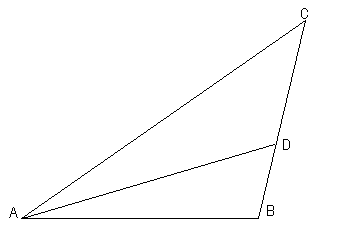
2. В треугольнике ABC AD- биссектриса, угол С равен 30⁰,

∠ BAD =22⁰. Найдите угол ADB.

3. Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если ∠ВОС = 114⁰.

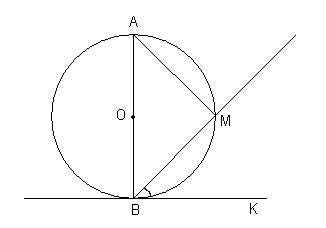
4. Отрезок АВ является диаметром окружности с центром О. Через точку В проведены касательная ВК и секущая ВМ. Докажите, что углы МВК и ВАМ равны.

Тема: Углы Вариант 6

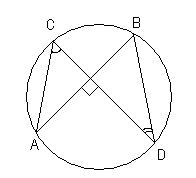
1. Точки А, В, С и D лежат на одной окружности так, что хорды АВ и СD взаимно перпендикулярны, а ∠АСD = 55⁰. Найдите величину угла ВDС.

2 . Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если ∠ВОС =127⁰. Ответ дайте в градусах.

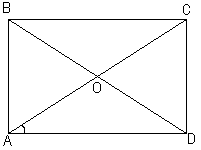
3. Диагональ прямоугольника образует с одной из его сторон угол, равный 34⁰. Найдите угол между прямыми, содержащими диагонали прямоугольника.

4. Отрезок АВ является диаметром окружности с центром О. Через точку В проведены касательная ВК и секущая ВМ. Докажите, что углы МВК и ВАМ равны.

Итоговый тест по теме: Углы

1.Хорда АВ стягивает дугу, равную 1600, а хорда АС – дугу в 600. Найдите угол ВАС.   1)700 , 2)1000, 3)1200, 4)1400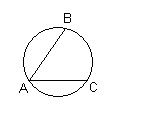

2.Найдите угол А, если угол С равен 320.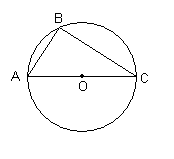

3.Один из углов параллелограмма на 20⁰ больше другого. Найдите наибольший угол параллелограмма (в градусах).

4. В окружности вписан равносторонний восьмиугольник. Найдите величину угла АВС .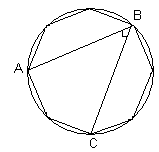

5.В угол величиной 50⁰ вписана окружность, которая касается его

сторон в точках А и В. На одной из дуг этой окружности выбрали точку С так, как показано на рисунке. Найдите величину угла АCВ.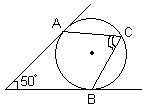

Вариант-1

6.В треугольнике АВС АВ=ВС, а внешний угол при вершине С равен 1230. Найдите величину угла В. Ответ дайте в градусах.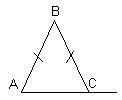

7.Сумма двух углов равнобедренной трапеции равна 96⁰. Найдите

больший угол трапеции. Ответ дайте в градусах.

8.Найдите величину угла DOB, если ОЕ – биссектриса угла АОС, OD – биссектриса угла СОВ.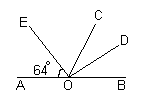

9.Укажите номера неверных утверждений:

1) Если один из углов, прилежащих к стороне параллелограмма, равен 50⁰, то другой угол, прилежащий к той же стороне, равен 40⁰.

2) Если вписанный угол равен 24⁰, то дуга окружности, на которую опирается этот угол, равна 48⁰.

3) Внешний угол треугольника равен сумме двух его внутренних углов.

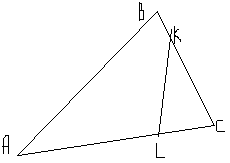
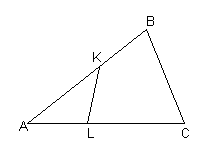
10. В треугольник АВС АС=18, АВ=12. Точки L и K отмечены на сторонах АС и АВ так, что АL= 6 и АК= 9. Докажите, что углы АВС и АLK равны.

Итоговый тест теме: Углы

1. Хорда АВ стягивает дугу, равную 140°, а хорда ВС – дугу 60°. Найдите угол АВС. А

В 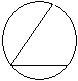С

1. Найдите угол С, если АВ = ВС.

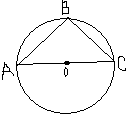
1. Один из углов параллелограмма на 40° больше другого.

Найдите наименьший угол параллелограмма (в градусах).

4.В окружность вписан равносторонний восьмиугольник. Найдите величину угла АВС (см. рисунок).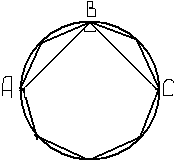

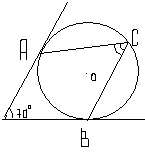
5.В угол величиной 70° вписана окружность, которая касается его сторон в точках А и В. На одной из дуг этой окружности выбрали точку С так, как показано на рисунке. Найдите величину угла АСВ.

Вариант 2

6.В треугольнике АВС АВ=ВС, а внешний угол при вершине С равен 132°. Найдите величину угла В. Ответ дайте в градусах.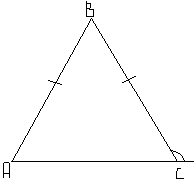

7.Сумма трёх углов равнобедренной трапеции равна 234°. Найдите меньший угол трапеции. Ответ дайте в градусах.

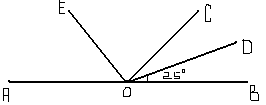
8.Найдите величину угла АОЕ, если ОЕ – биссектриса угла АОС, ОD – биссектриса угла СОВ, угол DOВ равен 25⁰ .

9.Укажите номера верных утверждений:

1) Если один из углов вписанного в окружность четырехугольника равен 63°, то противоположный ему угол четырехугольника равен 117°.

2) Если дуга окружности составляет 73°, то вписанный угол, опирающийся на эту дугу, равен 73⁰ ...

3) Противоположные углы параллелограмма равны...

10.В треугольнике АВС АС = 24, ВС = 12. Точки L и K отмечены на сторонах АС и ВС так, что LC = 4 и КС = 8. Докажите, что углы ВАС и LKC равны.