Обозначения и символика. Знакокодовая система обозначений.

Введение в курс.

Курс лекций Начертательная геометрияв которой рассматриваются следующие основные вопросы :

1) Построение изображений или чертежей предметов;

2) Решение геометрических задач в пространстве при помощи чертежей на плоскости.

Начертательная геометрия является лучшим средством развития у человека пространственного воображения, без которого не мыслимо инженерное творчество.

Основы этой науки заложены были при разработке первых чертежей. Дошедшие до нас чертежи и рисунки Древней Руси говорят о том, что при их создании применялись методы близкие к геометрическим методам. Древние памятники инженерной графики свидетельствуют, что графическое искусство на Руси было на высоком уровне.

Научное обоснование методов начертательной геометрии произошло в семнадцатом веке в связи с начавшемся бурным развитием в Европе промышленности. Основоположником считается видный французский ученый и политический деятель Гаспар Монж (1746 - 1818 гг.). Его учение о ортогональном методе проецированная сохранилось до нашего времени .

В России начертательную геометрию впервые стали изучать с 1810 года в Институте корпуса инженеров путей сообщения (С-Петербург), а с 1830 года стали преподавать во всех высших учебных заведениях России.

Первым русским ученым издавшим труд “Основания начертательной геометрии “ в 1821 году был профессор Р.А. Севастьянов.

Для изучения Начертательной геометрии в Московском автомобильно-дорожном институте студентами специальности ........................... можно рекомендовать следующие учебники и учебные пособия :

1) Кузнецов Н.С. Начертательная геометрия. М. “Высшая школа”,1969, 496 с.

2) Рыжов Н.Н. Главные позиционные задачи . Методические указания по курсу начертательной геометрии. М., МАДИ., 32 с.

3) Н.Н. Рыжов, О.А. Оганесов Задание поверхностей на комплексном чертеже (Методические указания к выполнению самостоятельной работы №1), МАДИ, Москва., 1990, 34 с.

4) Фролов С.А. Начертательная геометрия. М. “Машиностроение”, 1978, 240 с.

5) Луговой М.А., Ляшкевич П.А. , Оганесов О.А. , Фамин Л.Б. Тетрадь по начертательной геометрии для студентов специальностей ДМ, КМ, ТВ, ТУ, АП, ОД. М. 1995 г.

Обозначения и символика. Знакокодовая система обозначений.

Для обозначения геометрических фигур, их проекций , для краткой записи геометрических предложений , алгоритмов решения задач используется геометрический язык составленный из символов принятых в курсе математики.

Этот язык будет изучаться последовательно по мере изложения данного курса начертательной геометрии. Литература № 4 , с. 6 - 11. Знакокодовая система обозначений приведена в приложении 1 к данному конспекту лекций.

Метод проецирования .

Исходя из различных методов изображения начертательная геометрия содержит четыре основных раздела :

- ортогональные проекции;

- проекции с числовыми отметками;

- аксонометрические проекции;

- перспективные проекции.

Y ko

Биссектрису ОАо называют постоянной прямой ko эпюра Монжа.

Эта биссектриса позволяет установить связь между горизонтальной и профильными проекциями точки. Эта связь может быть установлена с помощью дуги окружности с центром в точке пересечения координатных осей.

Таким образом все проекции точки на комплексном чертеже находятся в проекционной связи.

Прямые соединяющие проекции точки меду собой называются линиями проекционной связи (А1,А2 или А2,А3).

Мы рассмотрели как зафиксировать положение точки в пространстве и отобразить это на комплексном чертеже. Точка относится к нульмерным геометрическим образам, не имеет измерений и не является материальной. На следующей лекции мы рассмотрим одномерные геометрические образы к которым относятся линии.

Линия имеет измерение вдоль, но не имеет толщины. При измерении длинны линии нам иногда потребуется вводить дополнительную плоскость проекций (в дополнение к уже рассмотренным : горизонтальной П1, фронтальной П2, профильной П3).

Линия .

Плоские кривые линии.

Среди плоских алгебраических кривых особо следует отметить кривые второго порядка.

Эти кривые иногда рассматривают как плоские сечения поверхностей - “конические сечения”.

Рассмотрим три простейших канонических формы : эллипс, гиперболу и параболу.

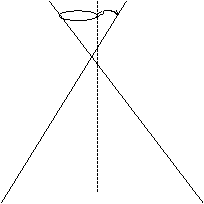
Зададимся конической поверхностью.

Т

Y

j Г 1

y

Эллипс

х F1· о F2·

· М

Окружность Г 2

1. Эллипс - j > y 2. Окружность - j = 90 град.

Эллипс геометрическое место точек М , сумма расстояний которых до двух заданных точек (F1, F2) называемых фокусами, есть величина постоянная.

Рассечем коническую поверхность плоскостью Г2 параллельной образующей конуса и не проходящей через вершину Т:

Г 1

Г 2

Т

Парабола - j = y

y

Двойная прямая

- Г 1 É Т j

Для получения гиперболы коническую поверхность необходимо рассечь плоскостью Г2 не проходящей через вершину конуса и не параллельную его образующей.

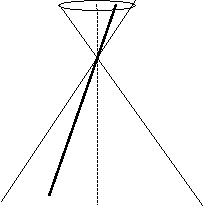Г 1 Г 2

Т

Две пересекающиеся прямые - Гипербола -

Г 1 É Т. j < y.

См. Л. с. 128 - 129.

Прямая линия и ее задание на комплексном чертеже.

Прямая линия - это простейший представитель семейства линий.

На комплексном чертеже прямая линия может быть задана непосредственно своими проекциями, проекциями двух точек принадлежащих прямой или следами.

При ортогональном проецировании на плоскость, не перпендикулярную ей, прямая проецируется в прямую линию.

Чтобы спроецировать отрезок прямой линии АВ на плоскость, из крайних точек отрезка опускают перпендикуляры на плоскость проекций и полученные проекции точек А1 и В 1 соединяют прямой которяй и будет проекцией данного отрезка.

Z

П 2 В 2

Т В

А2

А 1290

1

Х Ах В х

А1 90

В 1 П 1

Y

Одна проекция прямой не определяет ее положение в пространстве, так как может соответствовать множеству прямых расположенных в этой же проецирующей плоскости .

Необходимо иметь не менее двух проекций отрезка прямой, чтобы определить положение прямой в пространстве.

Отрезок АВ наклонен ко всем плоскостям проекций, поэтому проекции отрезка будут меньше его самого. Прямая наклоненная ко всем плоскостям проекций , называется прямой общего положения.

Рассмотрим прямоугольный треугольник D АВ1. Горизонтальная проекция

çА 1, В 1ç будет равна катету А,1 этого треугольника.

Чтобы определить величину второго катета В, 1 посмотрим на фронтальную плоскость проекций. Проекция на фронтальную плоскость В 2, 1 2 равна натуральной величине второго катета В, 1. Мы в этом дополнительно убедимся когда рассмотрим частное положение прямых в пространстве. Сейчас забегая вперед, я хочу обратить ваше внимание, что катет В,1 перпендикулярен горизонтальной плоскости проекций и параллелен фронтальной плоскости проекций.

Таким образом, зная два катета прямоугольного треугольника, мы можем найти его гипотенузу. Имея комплексный чертеж прямой общего пложения, где ни одна из проекций отрезка этой прямой не равна натуральной величине отрезка , мы всё

же можем найти его натуральную величину.

В 2

)

А 2 1 2

Х А х

А 1

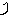
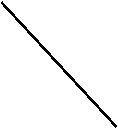Аоa

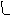
90 град В 1

Ü

В о

Если мы имеем чертеж с изображением отрезка в двух проекциях, то имеются все геометрические элементы для определения натуральной величины отрезка. Восстановим перпендикуляр к проекции А 1В 1 и на нем отложим расстояние равное В 2 1 2. Полученную точку В о соединим с горизонтальной проекцией А 1 точки А. Полученная гипотенуза будет натуральной величиной отрезка прямой АВ, а угол a будет натуральным углом наклона данного отрезка к горизонтальной плоскости проекций.

Без нахождения натуральной длинны отрезка нельзя найти угол наклона прямой к плоскости проекций . Поэтому если требуется найти углы наклона прямой ко всем плоскостям проекций (П 1, П2, П 3) , то необходимо определить натуральную длину отрезка на всех плоскостях проекций.

При подготовке к практическому занятию решите этим методом задачу 9 из Тетради.

Рассмотрим частные случаи расположения прямой в пространстве относительно плоскостей проекций.

Прямые уровня.

Это прямые параллельные плоскостям проекций.

Пряма параллельная горизонтальной плоскости проекций называется горизонтальной прямой уровня или горизонталью и обозначается h.

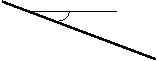
Все точки этой прямой находятся на одинаковом расстоянии от горизонтальной плоскости проекций ( на одном уровне) и поэтому ее легко узнать на чертеже - фронтальная проекция этой прямой всегда параллельна оси Х 1,2 , горизонтальная проекция отрезка этой прямой равна его натуральной величине.

ê А 1В 1ê= ê А ,В ê, êb 1 ê=êb ê; -угол наклона горизонтали к плоскости П 2 (фронтальной плоскости).

А 2 h 2 В2

Х 1,2

А1 b 1

h 1 В 1

Прямая, параллельная фронтальной плоскости проекций , называется фронтальной прямой уровня или фронталью ( f ). Горизонтальная проекция фронтали параллельна оси проекций Х 1,2 . Все точки фронтали находятся на одинаковом расстоянии от фронтальной плоскости проекций . Длинна фронтальной проекции отрезка фронтали равна его натуральной величине, а угол наклона фронтали к плоскости П 1 равен фронтальной проекции этого угла:

В 2

f 2

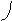А 2 a 2

Х 1,2

f 1

А1 В 2

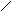
çА2, В2 ç= çА, Вç, а угол a = çf , П1ç = ç a 2 ç

Прямая параллельная профильной плоскости проекций , называется профильной прямой уровня. Горизонтальная (р 1) и фронтальная (р 2) проекции профильной прямой перпендикулярны оси проекций Х 1,2. Длина профильной проекции отрезка прямой равна его натуральной величине. Углы наклона к плоскостям проекций профильной проекции равны их натуральной величине.

êА з , В з ê = êА,В ê, êa з ê= êa ê, êb з ê = êb ê.

В 2 В з

р 2 b з р з

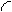А 2 a з А з

Х 0 Y

B 1

A 1

Y

Проецирующие прямые.

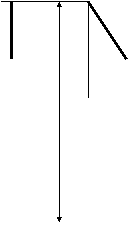
Прямая , перпендикулярная горизонтальной плоскости проекций , является горизонтально-проецирующей прямой. Отрезок этой прямой АВ.

Z

B2

K 3

E2 ·E 3º K 3

C2·D2

A2

X 0 Y

E1 K1

·

A2ºB2

С1

D1

Y

Фронтальная проекция такой прямой перпендикулярна оси Х . Проекция на горизонтальную плоскость называется основной проекцией. Горизонтальные проекции всех точек прямой совпадают с основной проекцией.

Прямая перпендикулярная фронтальной плоскости проекций называется фронтально-проецирующей. Она одновременно является горизонталью и профильной прямой, так как параллельна соответствующим плоскостям. Отрезок этой прямой С D.

Прямая, перпендикулярная профильной плоскости проекций , является профильно-проецирующей. Отрезок такой прямой ЕК. Эта прямая по отношению к плоскостям П1 и П 2 является одновременно горизонталью и фронталью.

Параллельные прямые.

Параллельные прямые - это прямые , лежащие в одной плоскости и никогда не пересекающиеся , сколько бы их не продлевали.

Параллельные прямые имеют параллельные одноименные проекции. Обычно по двум проекциям пары прямых можно сделать заключение о их параллельности,

однако если эти две прямые параллельны профильной плоскости проекций , то без рассмотрения третьей проекции прямых ничего утверждать нельзя.

С2 Z С3

В2 B3

D2 D2

А2 A3

X Y

А1 C1

В 2 D1

Y

Пересекающиеся прямые.

Это прямые лежащие в одной плоскости и имеющие одну точку пересечения.

Линии пересекающиеся в пространстве проектируются в виде пересекающихся проекций, причем проекции точки пересечения будут лежать на одной линии связи перпендикулярной оси Х.

К 2 a 2

b 2

Х

a 1

К1

b 1

Скрещивающиеся прямые.

Это прямые не параллельные и не пресекающиеся между собой. Эти прямые

не имеют общей точки и не лежат в одной плоскости.

12

3 2 º 4 2

a 2 22 b2

X 1.2

4 1

b 1

a 1 1 1 º 2 1 31

На рисунке приведен чертеж скрещивающихся прямых a·b . Эти прямые не имеют общих точек лежащих на одной линии связи. В этом случае нас будет интересовать какая прямая проходит выше, а какая ниже или какая прямая ближе к наблюдателю, а как дальше.Для этого рассмотрим точки у которых горизонтальные (1,2) или фронтальный (3,4) проекции совпадают, а другие нет. Такие точки называются конкурирующими. Этими точками пользуются для определения видимости.

Например, если посмотреть на горизонтальную проекцию прямых не ясно какая

точка выше 1 или 2 ? Однако, достаточно провести линию связи на фронтальную проекцию и вы увидите, что точка 1 принадлежащая прямой bнаходится выше, следовательно прямая b проходит выше прямой а.

Воспользовавшись точками 3 и4 определим какая из прямых ближе к нам.

Проведя линию проекционной связи видим , что точка 3 принадлежащая прямой b

ближе к нам и соответственно дальше от фронтальной плоскости проекций , чем

точка 4. Умение определять какая точка принадлежащая прямой или плоскости видима потребуется для решения последующих задач.

Проецирование прямого угла.

Прямой угол между двумя пресекающимися прямыми проецируется в натуральный размер только в том случае , когда одна из сторон угла параллельна плоскости проекций. Если одна сторона прямого угла будет параллельна фронталь-

ной плоскости проекций , то прямой угол будет проецироваться в натуральный

размер на фронтальную плоскость проекций.

Это имеет очень важное значение при построениях на комплексном чертеже

1) прямых перпендикулярных к друг к другу;

2) прямой перпендикулярной к плоскости ;

3) взаимно перпендикулярных плоскостей.

И соответственно, если ни одна из сторон прямого угла не занимает положение

прямой уровня, то угол не будет проектироваться в натуральную величину.

Решить задачу нахождения натуральной величины угла, в таком случае можно преобразовав комплексный чертеж.

( Подробно ”О Свойствах проекций плоских углов” читайте параграф 58 Н.Г.

С.А. Фролов)

Преобразование комплексного чертежа .

(Первая и вторая основные задачи преобразования чертежа).

Преобразование чертежа используется при решении задач связанных с измерениями геометрических образов или их взаимным расположением. Всего существует четыре основных задачи преобразования чертежа, две из которых связаны с преобразованием прямой линии и две с преобразованием плоскости.

Сформулируем две первые основные задачи :

1) преобразование комплексного чертежа таким образом, чтобы заданная на

чертеже прямая общего положения стала прямой уровня.

2) преобразование комплексного чертежа так, чтобы заданная на чертеже

прямая уровня заняла проецирующие положение.

Рассмотрим решение первой задачи на примере преобразования чертежа способом введения новой плоскости проекций. Способ введения новой плоскости проекций мы

уже применяли когда рассматривали комплексный чертеж точки.

Теперь рассмотрим этот способ применительно к линиям.

Пусть мы имеем два пересекающихся отрезка прямых общего положения .

Проведем такую замену плоскости проекций , чтобы одна из прямых стала прямой уровня. Это позволит нам судить под каким углом (тупым, прямым или острым )

пересекаются прямые . Причем, если этот угол не прямой, то для его измерения не достаточно будет одной замены плоскости проекций. В этом случае нам

потребуется , чтобы обе стороны угла были параллельны плоскости проекций.

С 2

А2 Ð?

= В2

\

Х 1,2

С 1

\

С 4 В4,С4 = В,С Ð?

А 1 a

В 1

В 4 Ð 90 град

=

А 4

Х 1,4

Введем новую плоскость проекций П 4 , так чтобы она была параллельна отрезку ВС. Одновременно плоскость П 4 перпендикулярна плоскости П 1.

Эти плоскости образуют новую ось Х 1,4. Ось на чертеже проводим

параллельно горизонтальной проекции отрезка В 1С 1.

Строим новую проекцию отрезка ВС:

1)é (В1,В4) É В 1 ; ( В 1, В4) ^ Х 1,4. (построить прямую В1,В4,

которая включает точку В 1 ; прямая перпендикулярна оси Х 1,4)

2) é В 4 Ì ( В1, В4) ; çВ 4, Х 1,4 ç = ç В 2, Х 1,2ç (построить точку В 4 принадлежащую прямой В1,В4 ; расстояние от В 4 до оси Х 1,4 равно расстоянию от В2 до оси Х 1,2.)

3) é (С1, С4) É С 1 ; ( С 1, С 4) ^ Х 1,4 ( построить линию С1,С4,

которой принадлежит точка С1; линию С1,С4 провести перпендикулярно

оси Х 1,4)

4) é С 4 Ì (С 1, С4) ; ê С4, Х 1,4 ê = ê С2, Х 1,2ê (построить точку С 4 принадлежащую прямой С1, С4; расстояние от точки С4 до оси Х 1,4

равно расстоянию от точки С2 до оси Х 1,2)

5) é ê В 4 С 4 êÉ В 4 Ù С 4 ( построить проекцию отрезка прямой В4,С4 включающего точки В4 и С4)

.

На этом этапе мы построили проекцию отрезка прямой В4,С4, которая обладает следующими метрическими свойствами :длина проекции отрезка равна длине

самого отрезка . Величина угла a 4 между проекцией В4,С4 и новой осью Х 1,4

равна углу наклона отрезка прямой В,С к плоскости П 1.

Чтобы закончить наши построения достаточно :

6)é (А1,А4) É А1 ; ( А 1,А4) ^ Х 1,4. (построить прямую А1,А4, которая включает точку А 1 ; прямая перпендикулярна оси Х 1,4)

7) é А 4 Ì ( А1, А4) ; çА 4, Х 1,4 ç = ç А 2, Х 1,2ç (построить точку А 4 принадлежащую прямой А1,А4 ; расстояние от А 4 до оси Х 1,4 равно расстоянию от А2 до оси Х 1,2.)

8) é êА 4, В 4 êÉ А 4 Ù В 4 ( построить проекцию отрезка прямой А4,В4 включающего точки А4 и В4).

Теперь мы построили проекцию угла А4В4С4 на плоскость П4 , причем проекция

равна натуральной величине угла АВС, так как это прямой угол.

Рассмотрим решение второй основной задачи преобразования чертежа

на примере:

Изобразим на чертеже горизонталь h.

Необходимо ввести новую плоскость проекций так, чтобы по отношению к ней горизонталь заняла проецирующие положение, т. е. спроецировалась в точку.

Так как данная прямая параллельна горизонтальной плоскости проекций , то

для того чтобы она спроецировалась в точку в точку необходимо заменить

фронтальную плоскость проекций на новую П4 :

П4 ^ П1 Ù ^ АВ.

А 2 h 2 В 2

_ _

Х 1,2

А 1 h 1

В 2

/

h 3 º · А4 º В 4

Х 1,4

Для всех точек линии АВ (горизонтали) будет одна линия проекционной связи перпендикулярная оси Х 1,4, а расстояние от горизонтали до горизонтальной

плоскости проекций все одинаковы. Измерим расстояние на плоскости П 2 и

отложим его от оси Х 1,4 по линии проекционной связи. Проекция на плоскость П4 будет обладать собирательным свойством .

Если бы прямая занимала общее положение , то преобразовать ее в прямую проецирующую можно двумя заменами, т. е. обе задачи решают последовательно.

В качестве литературы по данному разделу рекомендую учебное пособие

М.А. Луговой Точка, прямая, плоскость. МАДИ, Москва 1995 г.

При подготовке к практическому занятию прошу решить задачи 6, 7, 10 из Тетради.

Точка в плоскости.

Точка принадлежит плоскости, если лежит на прямой принадлежащей плоскости.

Пусть плоскость задана пересекающимися прямыми а и b.

Имеется горизонтальная проекция точки А1 необходимо построить А2.

a 2

12

22

· A2

B 2

B 1

*А1

A1 1 1 21

Через горизонтальную проекцию точкиа1 проведем произвольную прямую пересекающую горизонтальные проекции линий задающих плоскость

в точках 1 1 и 2 1. Построим фронтальную проекцию этой линии и на ней найдем точку а 2.

Подумайте самостоятельно, как бы мы решали аналогичную задачу, если бы были заданы обе проекции точки А и требовалось определить принадлежит ли точка А плоскости заданной пересекающимися прямыми.

Дома самостоятельно, на листе в клетку в тетради для конспектов построить эллипс. Большую и малые оси задать произвольно. Прошу не строить овал вместо эллипса.

Параллельные плоскости.

Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Поэтому, если требуется через точкуDпровести плоскость параллельную заданной АВС, то через точку проводят две прямые, параллельные любым прямым, находящимся в заданной плоскости.

В2

D2 ·

А2

С2

С 1

D1·

А1

В1

Пересекающиеся плоскости.

Если плоскости не параллельны, то они обязательно пересекутся.

Если плоскости занимают частное положение в пространстве, то положение линии пересечения определить довольно просто.

Например, подумайте какое положение в пространстве займет линия пересечения двух горизонтально проецирующих плоскостей ?

S

T

Õ 1

Рассмотрим случай когда плоскость общего положения пересекается с плоскостью параллельной плоскости П1, т.е. с горизонтальной плоскостью.

Априори можно утверждать, что линия пересечения будет горизонтальной прямой. Действительно, линия пересечения принадлежит одновременно плоскости общего положения и горизонтальной плоскости, а все линии принадлежащие горизонтальной плоскости являются горизонталями.

Аналогичные рассуждения можно привести рассматривая пересечение плоскости общего положения и фронтальной плоскости. Линия пересечения будет фронталью. Запомним это.

А теперь рассмотрим наиболее сложный случай пересечения двух плоскостей общего положения.

В2 D2

T 2 12 22 72 32 E2