Определение и основные свойства параллелограмма

Начнем с того, что вспомним определение параллелограмма.

Определение. Параллелограмм– четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).

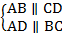
Рис. 1. Параллелограмм

Вспомним основные свойства параллелограмма:

Для того, чтобы иметь возможность пользоваться всеми этими свойствами, необходимо быть уверенным, что фигура, о которой идет речь, – параллелограмм. Для этого необходимо знать такие факты, как признаки параллелограмма. Первые два из них мы сегодня и рассмотрим.

Первый признак параллелограмма

Теорема.Первый признак параллелограмма.Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник –параллелограмм. .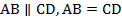

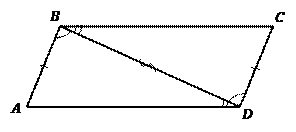
Рис. 2. Первый признак параллелограмма

Доказательство. Проведем в четырехугольнике диагональ 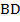(см. Рис. 2), она разбила его на два треугольника. Запишем, что мы знаем об этих треугольниках:

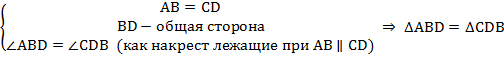
по первому признаку равенства треугольников.

Из равенства указанных треугольников следует, что 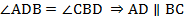по признаку параллельности прямых при пересечении их секущей. Имеем, что:

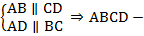параллелограмм по определению. Что и требовалось доказать.

Доказано.

Второй признак параллелограмма

Теорема. Второй признак параллелограмма.Если в четырехугольнике каждые две противоположные стороны равны, то этот четырехугольник –параллелограмм. .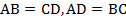

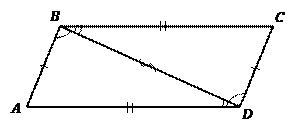
Рис. 3. Второй признак параллелограмма

Доказательство. Проведем в четырехугольнике диагональ 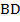(см. Рис. 3), она разбивает его на два треугольника. Запишем, что мы знаем об этих треугольниках, исходя из формулировки теоремы:

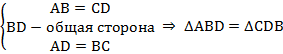по третьему признаку равенства треугольников.

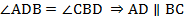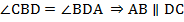Из равенства треугольников следует, что и по признаку параллельности прямых при пересечении их секущей. Получаем:

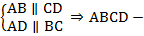параллелограмм по определению. Что и требовалось доказать.

Доказано.

Пример на применение первого признака параллелограмма

Рассмотрим пример на применение признаков параллелограмма.

Пример 1. В выпуклом четырехугольнике 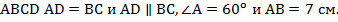Найти: а) углы четырехугольника; б) сторону .

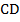Решение. Изобразим Рис. 4.

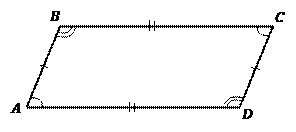
Рис. 4

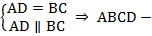параллелограмм по первому признаку параллелограмма.

А. 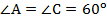по свойству параллелограмма о противоположных углах, 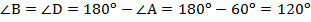по свойству параллелограмма о сумме углов, прилежащих к одной стороне.

Б. 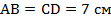по свойству равенства противоположных сторон.

Ответ. .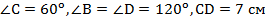

На следующем уроке мы рассмотрим еще один признак параллелограмма (третий).

Домашнее задание

1. Докажите, что если сумма углов, прилежащих к любой из сторон четырехугольника, равна 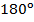, то этот четырехугольник – параллелограмм.

2. Точк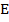и и 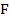– соответственно середины сторон 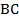и 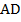параллелограмма . Докажите, что четырехугольник 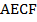– параллелограмм.

3. В треугольнике 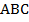медиана 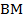перпендикулярна к стороне 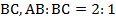. Найдите .

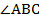Урок 8: Третий признак параллелограмма

Данный урок посвящён третьему признаку параллелограмма и его применению. На предыдущем уроке были изучены первый и второй признаки параллелограмма, которые основывались на свойствах сторон и углов параллелограмма. Третий признак основан на свойстве диагоналей параллелограмма. А именно, на том, что диагонали параллелограмма в точке пересечения делятся пополам. Признаки параллелограмма очень важны при решении целого ряда задач, поскольку позволяют доказывать то, что четырёхугольник является параллелограммом, а, значит, можно пользоваться его свойствами.