Второе свойство параллелограмма
Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.
Дано:
– параллелограмм ( 
).
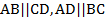Доказать: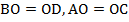 
(см. Рис. 3).
Доказательство:
Проведем диагонал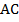и 
и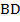 
и отметим их точку пересечения: 
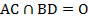. Рассмотрим треугольник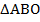и 
и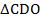 
.
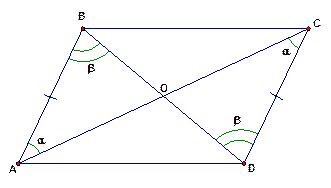
Рис. 3
Они равны по второму признаку равенства треугольников (стороне и двум прилежащим к ней углам). Действительно:
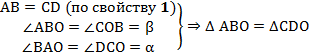(по 2-му признаку равенства треугольников)
Равенство углов вновь следует из того, что они являются внутренними накрест лежащими при соответствующей секущей и параллельных прямых (которыми являются противоположные стороны параллелограмма по определению). Противоположные стороны равны по доказанному выше свойству 1.
Из равенства треугольников следует равенство соответствующих элементов. Значит: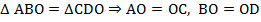 
.
Доказано.
Доказанные свойства параллелограмма позволяют решать многочисленный класс задач. Разберём несколько примеров.
Примеры задач на свойство параллелограмма
Пример 1.
Периметр параллелограмма равен 48 см. Найти его стороны, если одна сторона на 3 сантиметра больше другой (см. Рис. 4).
Дано:
– параллелограмм,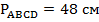 
. 
.
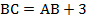Найти:
Решение:
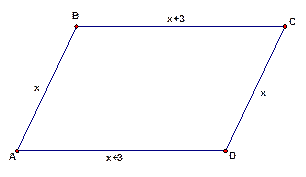
Рис. 4
Обозначим меньшую сторону параллелограмма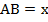 
. Учитывая свойство 1 для параллелограмма, запишем следующее равенство: 
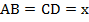. Из условия: 
.
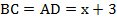Напомним, что периметр многоугольника – это сумма всех его сторон. Поэтому можем записать следующее равенство: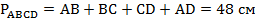 
.
Или: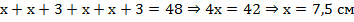 
.
Получаем, что стороны параллелограмма: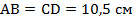 
, 
.
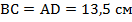Ответ: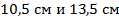 
.
Пример 2
Биссектриса угла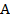 
параллелограмма пересекает сторону 
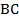в точке 
. 
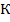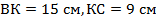. Найдите периметр параллелограмма.
Дано:
– параллелограмм,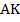 
– биссектриса. 
. .
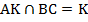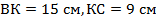Найти:
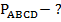
Решение:
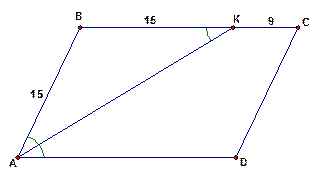
Рис. 5
Вспомним определение биссектрисы: биссектриса делит угол пополам. Это значит, что: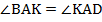 
. Кроме того, 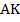является секущей при параллельных прямых 
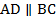. А это значит, что внутренние накрест лежащие углы равны: 
.
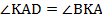Из этого получается:
.
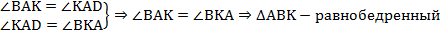Так как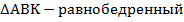 
, то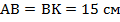 
. Откуда: 
.
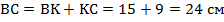Периметр – сумма всех сторон, у параллелограмма противоположные стороны равны. Получаем: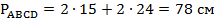 
.
Ответ: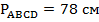 
.
Итак, мы рассмотрели определение и свойства параллелограмма, в частности: равенство противоположных сторон и углов, а также то, что диагонали параллелограмма точкой пересечения делятся пополам, и использовали эти свойства при решении задач.
В дальнейшем мы изучим признаки параллелограмма, а также научимся применять свойства и признаки параллелограмма при решении более сложных примеров.
Домашнее задание
1. Найдите периметр параллелограмма , если сторона 
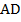равна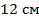 
и составляет 
стороны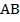 
.
2. Периметр параллелограмма равен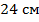 
. Найдите стороны параллелограмма, если одна из них на 
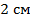больше другой.
3. Найдите углы параллелограмма, если градусные меры двух его углов относятся как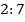 
.
4. Точка пересечения диагоналей параллелограмма удалена от двух его вершин на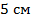 
и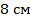 
. Найдите длины диагоналей параллелограмма.
Урок 7: Признаки параллелограмма
На сегодняшнем уроке мы повторим основные свойства параллелограмма, а затем уделим внимание рассмотрению первых двух признаков параллелограмма и докажем их. В ходе доказательства вспомним применение признаков равенства треугольников, которые мы изучали в прошлом году и повторяли на первом уроке. В конце будет приведен пример на применение изученных признаков параллелограмма.