Параллельными называются такие прямые, которые не пересекаются.
–прямые, с – секущая.
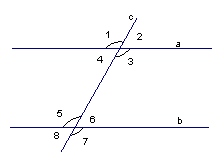
Рис. 1
Возникает много углов (1, 2, 3, 4, 5, 6, 7, 8).
Эти углы важны для нас, и поэтому они имеют названия:
- накрест лежащие углы: 
3 и 5, 4 и 6;
- односторонние углы: 4 и 5, 3 и 6;
- соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Основные теоремы о параллельности прямых:
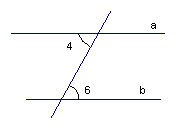
Рис. 2
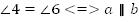
Если накрест лежащие углы равны, то прямые параллельны. И наоборот, если прямые параллельны, то накрест лежащие углы равны.
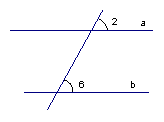
Рис. 3
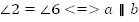
Если соответственные углы равны, то прямые параллельны. И наоборот, если прямые параллельны, то соответственные углы равны.
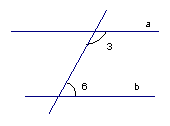
Рис. 4
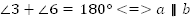
Если сумма внутренних углов равна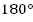 
, то прямые параллельны. И наоборот, если прямые параллельны, то сумма внутренних углов равна .
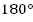Рассмотрим некоторые типовые задачи на признаки параллельности прямых.
Задача 1
Задача 1:
Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210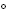 
. Найдите эти углы.
Дано: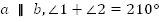 
.
Найти: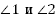 
.
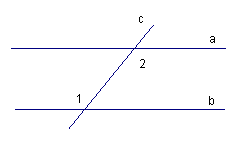
Рис. 5
Решение:
Поскольку прямые a и b параллельны, то накрест лежащие углы равны.
Следовательно,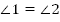 
.
Тогда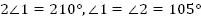 
.
Ответ: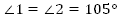 
.
Задача 2
Задача 2:
Найдите все углы, образованные при пересечении параллельных прямых a и b с секущей c, если:
А. один из углов равен 
;
Б. один из углов на 
больше другого.
Рис. 6
А.
Дано: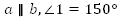 
.
Найти: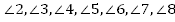 
.
Решение:
1. 
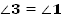(как вертикальные);
2. 
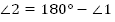(как смежные);
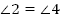(как вертикальные);
;
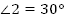3. 
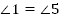и 
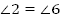(как соответственные)
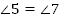и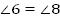 
(как вертикальные)
Ответ: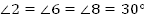 
, 
.
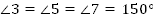Б.
Дано: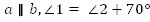 
.
Найти: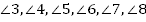 
.
Решение:
1. 
+
, 
.
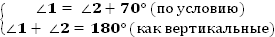
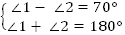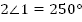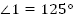Тогда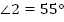 
.
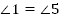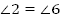2. и (как соответственные)
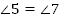и 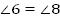(как вертикальные)
Ответ: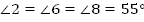 
, 
.
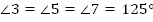Задача 3
Задача 3:
На рисунке 
, прямые m и n – биссектрисы углов 1 и 2. Докажите, что 
.
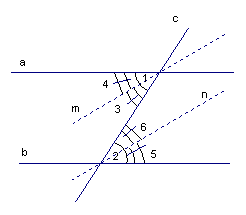
Рис. 7
Доказательство:
Из того, что , по свойству параллельных прямых вытекает, что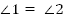 
.
Следовательно, углы 3, 4, 5, 6 тоже будут равны между собой, как половинки равных углов.
Тогда из того, что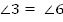 
, по первому признаку параллельности прямых 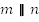, что и требовалось доказать.
Домашнее задание
1. Докажите, что биссектрисы соответственных углов при параллельных прямых параллельны.
2. Две параллельные прямые пересечены третьей прямой так, что сумма двух из полученных восьми углов равна 240 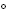. Найдите меры всех образованных углов.
3. Через точку, не лежащую на прямой a, проведено три прямые. Докажите, что по крайней мере две из них пересекают прямую a.
Урок 3: Повторение. Треугольники.
На этом уроке мы повторим основные понятия, пройденные в 7 классе. К ним относятся: важнейшая геометрическая фигура – треугольник, его свойства, признаки равенства треугольников. Для повторения основных фактов, связанных с треугольниками, нам необходимо будет вспомнить понятия, возникающие при рассмотрении пересечения секущей двух параллельных прямых, такие как накрест лежащие, односторонние, соответственные и вертикальные углы. Исходя из этих понятий, мы повторим теоремы о сумме углов треугольника и о внешнем угле треугольника. В ходе урока рассмотрим примеры.