Понятие многоугольника. Виды многоугольников. Свойства выпуклых многоугольников.
Определение 1. Ломаной линией называется конечная последовательность отрезков, такая, что один из концов первого отрезка служит концом второго, другой конец второго отрезка служит концом третьего и т. п.
Отрезки, составляющие ломаную линию, называются звеньями. Соседние отрезки не лежат на одной прямой. Если концы ломаной совпадают, то она называется замкнутой. Ломаная может пересекать сама себя, касаться сама себя и налегать сама на себя. Если таких особенностей у ломаной нет, то она называется простой.
Определение 2. Простая замкнутая ломаная вместе с частью плоскости, ограниченной ею, называется многоугольником.
Сама ломаная при этом называется границей многоугольника, звенья ломаной – сторонами многоугольника, концы звеньев – вершинами многоугольника. Две соседних стороны многоугольника образуют угол. Число углов в многоугольнике равно числу сторон. У каждого многоугольника есть углы меньше 180°. Стороны и углы многоугольника называют элементами многоугольника.
Отрезок, соединяющий две несоседние вершины многоугольника, называется диагональю. В любом n-угольнике можно провести n-2 диагонали.
Определение 3. Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону. Многоугольники, не отвечающие этому условию, называются невыпуклыми.
Свойства выпуклых многоугольников.
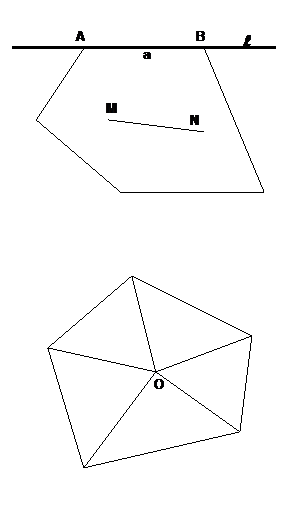 Свойство 1. У выпуклого многоугольника все углы меньше 180°.
Свойство 1. У выпуклого многоугольника все углы меньше 180°.
Доказательство: Возьмем любой угол А выпуклого многоугольника Р и его сторону а, идущую из вершины А. Пусть l - прямая, содержащая сторону а. Так как многоугольник Р выпуклый, то он лежит по одну сторону от прямой l. Поэтому угол А лежит по одну сторону от прямой l. Следовательно, угол А меньше развернутого, т. е. ÐA < 180°.
Свойство 2. Отрезок, соединяющий любые две точки выпуклого многоугольника, содержится в этом многоугольнике.
Доказательство: Возьмем любые две точки М и N выпуклого многоугольника Р. Многоугольник Р является пересечением нескольких полуплоскостей. Отрезок MN лежит в каждой из этих полуплоскостей. Поэтому он содержится и в многоугольнике Р.
Свойство 3. Сумма углов выпуклого многоугольника равна (n – 2)∙180°.
Доказательство: Возьмем внутри выпуклого многоугольника Р произвольную точку О и соединим ее со всеми вершинами многоугольника. Образуется n треугольников, сумма углов каждого из которых равна 180°. Углы при вершине О в сумме дают 360° = 2∙180°. Поэтому сумма углов многоугольника равна n∙180° - 2∙180° = (n – 2)∙180°.
Понятие параллелограмма. Свойства параллелограмма.
Определение 1. Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом.
У каждого параллелограмма четыре вершины, четыре стороны, четыре угла. Две стороны, имеющие общие концы, называются смежными. У каждого параллелограмма две диагонали – отрезки, соединяющие противоположные вершины параллелограмма. Сумма углов параллелограмма равна 360°.
Свойства параллелограмма.
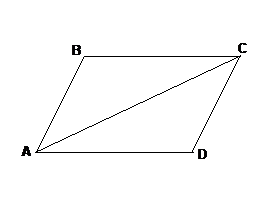 Свойство 1. У параллелограмма противоположные стороны равны и противоположные углы попарно равны.
Свойство 1. У параллелограмма противоположные стороны равны и противоположные углы попарно равны.
Доказательство: Проведем диагональ АС. АС – общая;
ÐВАС = ÐАСD (внутренние накрест лежащие при АВ II BC и секущей АС);
ÐВСА = ÐСАD (внутренние накрест лежащие при АD II BC и секущей АС);
Þ DАВС = DАDС (по 2 признаку).
АВ = CD; BC = AD; ÐВ = ÐD.
ÐА = ÐВАС + ÐСAD; ÐС = ÐАСB + ÐАСD; Þ ÐА = ÐС.
Свойство 2. У параллелограмма углы, прилежащие к одной стороне, в сумме дают 180°.
Доказательство:
ÐВ + ÐА =180° (внутренние односторонние при ВС II AD и секущей АB).
ÐB + ÐС =180° (внутренние односторонние при AВ II CD и секущей BC).
ÐD + ÐC =180° (внутренние односторонние при ВС II AD и секущей CD).
ÐA + ÐD =180° (внутренние односторонние при AВ II CD и секущей AD).
Свойство 3. Диагонали параллелограмма точкой пересечения делятся пополам.
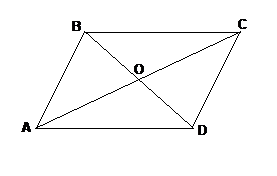 Доказательство: Проведем диагонали АС и BD, пересекающиеся в точке О.
Доказательство: Проведем диагонали АС и BD, пересекающиеся в точке О.
АВ = СD (по первому св-ву параллелограмма);
ÐAВO = ÐODC (внутренние накрест лежащие при АВ II CD и секущей BD);
ÐВАO = ÐOСD (внутренние накрест лежащие при АB II CD и секущей АС);
Þ DАВO = DODС (по 2 признаку).
ВO = OD; AO = OC.
Признаки параллелограмма.
Признак 1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм.
 Дано: ABCD – четырехугольник; АD II BC,
Дано: ABCD – четырехугольник; АD II BC,
АD = BC.
