Организация деятельности учащихся при выработке умений выводить логические следствий.

Каждому ребенку дарована от природы склонность к познанию и исследованию окружающего его мира. Правильно поставленное обучение должно совершенствовать эту склонность, способствовать развитию соответствующих умений и навыков. Эффективность исследовательской деятельности зависит и от меры увлеченности ученика этой деятельностью, и от умения ее выполнять. Представляется необычайно полезным прививать школьникам вкус к исследованию, вооружать их методами научно – исследовательской деятельности.

Необходимо при этом, чтобы ученики:

а) владели определениями, терминами и обозначениями, используемыми в формулировке и доказательстве теоремы;

б) приняли посильное участие в составлении ее формулировки;

в) освоили формулировку, выделили условие и заключение;

г) освоили первые шаги (умели сделать чертеж как можно более близким к условию, внести в него все, что дано в условии, ввести необходимые обозначения, записать условие и заключение, используя выделенные обозначения.

Существенную роль в усилении прикладной и практической направленности курса геометрии и одновременно в развитии способностей учащихся к самостоятельным исследованиям играют задания, выполнение которых представляет собой относительно завершенный исследовательский цикл: наблюдение – гипотеза – проверка гипотезы.

Выполняя исследования, ученики развивают также и навыки использования инструментов. Очень важно так организовать учебную работу детей, чтобы они ненавязчиво усваивали бы процедуру исследования, последовательно проходя все его основные этапы: - мотивация исследовательской деятельности:
- постановка проблемы;
- сбор фактического материала;
- систематизация и анализ полученного материала;
- выдвижение гипотез;
- проверка гипотез;
- доказательство или опровержение гипотез.

И здесь задача учителя найти простые и удобные средства для практической реализации каждого из названных этапов. Изложение в учебнике по необходимости краткое. Объявляется теорема, следом идет доказательство. Но урок – это не пересказ учебника. Перед учителем возникают вопросы: как подвести учеников к теореме, новому понятию, привлечь их внимание? Не заинтересуешь – не будут слушать и ничего не усвоят. Сообщить готовое быстрее, чем открывать его вместе с учениками. Но от «прослушанного» как известно, через две недели в памяти остается не более 20%. Не обернется ли такая «экономия» перегрузками, когда придется десять раз повторять? Самостоятельное открытие теорем вызывает интерес у учеников. Материал усваивается глубже, укрепляется желание к познанию нового, развивается мышление. Чтобы ученики могли принять участие в выдвижении гипотезы, в открытии некоторого свойства, учитель должен предложить специальные подготавливающие вопросы и задачи. Возможно, первая попытка ученика сформулировать теорему окажется не очень удачной. С помощью примеров и контрпримеров учитель помогает уточнить формулировку, доказать необходимость каждого условия теоремы. Вызывают интерес вопросы учителя, заданные с целью заронить сомнение в справедливости теоремы. Подготавливающие задачи и вопросы имеют большое значение. Рассмотрение некоторой задачи помогает учителю убедить класс в необходимости доказательства теоремы. Иногда решение задачи является частью доказательства. Бывает, что теорема является логическим следствием рассмотренной задачи. Может показаться, что использование подготавливающих задач отнимает много времени. Но одна из главных целей обучения математики – обучение решению задач, а подготавливающая задача – это новая задача и , как правило, нестандартная. Решение этих задач, кроме подготовки к освоению теоремы, еще и развивает мышление, учит поиску решения. Подготавливающие задачи не только облегчают понимание теории, но и позволяют достичь глубокого ее усвоения.

Целесообразно обратить внимание учеников на первые шаги доказательства (сделать чертеж, ввести обозначения, выделить и записать условие и заключение), подчеркнуть их значение. Если все ученики овладевают первыми шагами, то это существенно облегчит доказательство теорем.

Многие ученики считают излишним записывать условие и требование задачи. Сообщить готовое быстрее, чем открывать его вместе с учениками. Но от «прослушанного» как известно, через две недели в памяти остается не более 20%. Не обернется ли такая «экономия» перегрузками, когда придется десять раз повторять? Самостоятельное открытие теорем вызывает интерес у учеников. Материал усваивается глубже, укрепляется желание к познанию нового, развивается мышление. Чтобы ученики могли принять участие в выдвижении гипотезы, в открытии некоторого свойства, учитель предлагает специальные подготавливающие вопросы и задачи. Возможно, первая попытка ученика сформулировать теорему окажется не очень удачной. С помощью примеров и контрпримеров учитель помогает уточнить формулировку, доказать необходимость каждого условия теоремы. Вызывают интерес вопросы учителя, заданные с целью заронить сомнение в справедливости теоремы.

Подготавливающие задачи и вопросы имеют большое значение. Рассмотрение некоторой задачи помогает учителю убедить класс в необходимости доказательства теоремы. Иногда решение задачи является частью доказательства. Бывает, что теорема является логическим следствием рассмотренной задачи. Может показаться, что использование подготавливающих задач отнимает много времени. Но одна из главных целей обучения математики – обучение решению задач, а подготавливающая задача – это новая задача и , как правило, нестандартная. Решение этих задач, кроме подготовки к освоению теоремы, еще и развивает мышление, учит поиску решения. Подготавливающие задачи не только облегчают понимание теории, но и позволяют достичь глубокого ее усвоения. Целесообразно обратить внимание учеников на первые шаги доказательства (сделать чертеж, ввести обозначения, выделить и записать условие и заключение), подчеркнуть их значение. Если все ученики овладевают первыми шагами , то это существенно облегчит доказательство теорем. Многие ученики считают излишним записывать условие и требование задачи. Нужно их убедить, что, не используя условие, нельзя решить задачу или доказать теорему. Требование мы записываем, чтобы видеть цель. Когда не удается решить задачу или доказать теорему нередко причина состоит в том, что не использовано условие или упущена из вида цель.

Пример 11 [29]

Рассмотрим урок по теме “ Теорема о сумме углов треугольника”

с использованием элементов исследования.

Тема: “ Теорема о сумме углов треугольника ”

Цели урока:

• сформулировать и доказать теорему о сумме углов треугольника;
• формировать умение анализировать, обобщать, использовать элементы исследования; развивать внимание, мышление, математическую речь.

Оборудование:доска, линейка, плакат, карточки - треугольников.

Ход урока

(мотивация)На предыдущих уроках мы с вами изучали признаки и свойства параллельности прямых. И сегодня на уроке, полученные по этой теме знания, помогут сделать открытие. Фигура, с которой мы будем работать, вам уже знакома. А сегодня мы найдем сумму всех ее углов.

(сбор фактического материала)

1) Сформулируйте определение треугольника.

(Треугольник – это фигура, образованная тремя точками, не лежащими на одной прямой, и отрезками, попарно соединяющими эти точки.)

2) Назовите элементы треугольника. (Вершины, стороны, углы.)

3) Какие треугольники различают? (По сторонам: разносторонние, равносторонние, равнобедренные; карточки – треугольники)

4) Треугольники различают и по углам. Давайте с вами составим рассказ по теме « Угол».

Для помощи используем план, записанный на доске.

1. 1. Угол – это фигура, …

2. Если …, то угол называют …

3. Внутренний угол треугольника – это …

Ответы:

1. Угол – это фигура, образованная двумя лучами, выходящими из одной точки. Лучи называют сторонами угла, а точку – вершиной.

2. Если величина угла 90⁰, то угол называют прямым.

Если – 180⁰, то развернутым. Если больше 0⁰. но меньше 90⁰, то называют острым. Если больше 90⁰, но меньше 180⁰, называют тупым. Т.о. углы бывают тупые, острые, прямые и развернутые.

3. Внутренний угол треугольника – угол, образованный его сторонами, вершина треугольника является вершиной его угла.

Значит, в треугольнике углы могут быть различными: тупыми, острыми и прямыми.

5)Начертите угол: (1 ученик делает на доске)

1 – ряд – тупой; 2 – ряд – прямой; 3 – ряд острый.

Дополните рисунок до треугольника. Что для этого нужно сделать?

(Взять по точке на сторонах угла и соединить их отрезками.)

6) Полученные треугольники можно назвать: тупоугольными, прямоугольными и остроугольными. (карточки – треугольники)

Обратите внимание, что у остроугольного треугольника все углы острые.

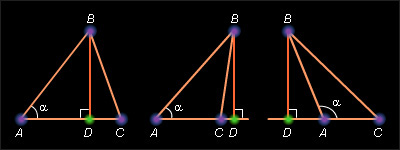
7)Бывают ли треугольники с двумя прямыми углами? С двумя тупыми углами? С прямым и тупым углом? Как это обосновать? Сделать рисунок. К доске выходит ученик и выполняет следующие рисунки:

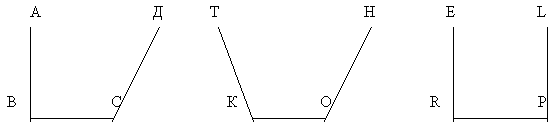
Далее идет коллективное обсуждение.

(исследование)

Лучи ВА и СО, КТ и ОН. КЕ и PL пересекаются, значит, треугольник не получится. Сумма односторонних углов в I случае больше, чем 180⁰ , во II случае также больше, чем 180⁰ , а в III случае — равна 180°. В III случае прямые параллельны, а в первых двух случаях прямые расходятся. Делают вывод, что треугольник не может иметь два тупых или два прямых угла. А также в треугольнике не может быть одновременно один тупой и один прямой углы.

(постановка проблемы)

8) Мы выполнили некоторую практическую работу, сделали обоснование того факта, что треугольник не всегда существует. Его существование зависит от величин углов. Как можно узнать, чему равна сумма углов треугольника? Практически — измерение, теоретически — рассуждением

9) На дом вам было дано задание: построить треугольники, измерить их углы и найти сумму углов каждого треугольника. Чему равна сумма углов каждого треугольника? (180°, 179°, 182°, 185°, 178°...)

Что заметили? Все суммы близки к 180°. Значит, сумма углов треугольника равна 180⁰.

(выдвижение гипотезы)

10) Итак, ребята, у вас появилась гипотеза, сумма углов треугольника равна 180 . Однако, у многих из вас получились результаты, близкие к 180°, но не 180°, Почему? Измеряя, мы получаем приближенные значения. Сумма углов треугольника была практическим путем установлена, вероятно, еще в Древнем Египте, Прокл утверждал, что доказательство этого факта было известно еще в V в. до н. э. Однако у нас с вами есть гипотеза: сумма углов треугольника равна 180 , которую можно проверить еще одной практической работой: где еще сегодня называли это число? Величина развернутого угла.

(систематизация и анализ полученного материала)

На столах лежат треугольники. Путем перегибания соберем углы треугольника в одну точку.

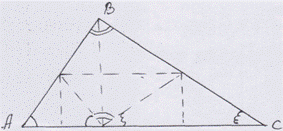
Что у нас получилось? Что сумма углов треугольника равна 180⁰.

11) Более точно это можно доказать, используя теорему о сумме внутренних углов треугольника - одну из самых важных теорем геометрии. Записать название темы.

( проверка гипотезы)

Сформулируйте теорему: Сумма углов треугольника равна 180⁰

Попробуем доказать теорему, “собрав” все углы треугольника в одну вершину (на доске выполняется чертеж).

А

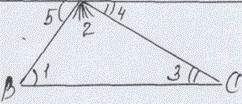
“ Собрать углы” - значит, “ взять углы”, равные данным.

Когда < 4=<3 (< 5=<1)? (При параллельности прямой а и стороны ВС)

Известно:

<5 + <2 + <4 =180°. (развернутый угол)

<1 + <2+ <3 = 180°.

(доказательство или опровержение гипотез)

12) Доказать теорему , делая кратную запись:

ДАНО: 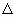АВС,<1, <2, <3 - внутренние.

ДОКАЗАТЬ: <1 + <2 + <3 = 180°.

Доказательство:

1) Проведем прямую а // ВС, А 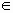а.

2) <5 = <1 (внутренние накрест лежащие при а // ВС и секущей АВ)

<4 = <3 ((внутренние накрест лежащие при а // ВС и секущей АС)

3) <5 + <2 + <4 = 180°. (развернутый угол)

4) <1 + <2 + <3 = 180°. Ч. Т. Д.

13) Повторить план доказательства:

- провести прямую через одну из вершин параллельно противолежащей стороне;
- составить пары равных углов;
- представить развернутый угол в виде суммы углов;
- заменить слагаемые равными им углами треугольника.

14) Записать теорему и доказательство в тетрадь.

15) Что утверждает новая теорема? сумма углов треугольника равна 180°. Значит, в треугольнике может быть только один тупой угол, только один прямой угол.

16) Чему равен третий угол в треугольнике, если один из углов 30°, второй 100°? (50°)

17) Чему равен угол равностороннего треугольника? (60)

18) Чему равна сумма острых углов прямоугольного треугольника? (90°)

19) Чему равен острый угол прямоугольного равнобедренного треугольника? (45) Последние три утверждения - ответы на вопросы - вытекают (следуют) из теоремы, т. е. являются следствиями из теоремы.

Повторить следствия. Иллюстрируя чертежами (ученики делают схематические чертежи в тетрадях)

20) ДОМА п. 30 стр. 66; № 223, 225,228. Придумать задачу на применение новой теоремы.

Самостоятельная работа.

ВАРИАНТ 1.

1. Один из углов равнобедренного треугольника равен 96⁰. Найдите два других угла треугольника.

2. В треугольнике СДЕ с углом, равным 32⁰, проведена биссектриса СК, < СКД =72⁰. Найдите <Д.

3. В равнобедренном треугольнике MNP с основанием МР и углом N, равным 64⁰, проведена высота МН. Найдите < МРН.

ВАРИАНТ 2.

1. Один из углов равнобедренного треугольника равен 108⁰. Найдите два других угла треугольника.

2. В треугольнике СДЕ проведена биссектриса СК, <Д=68⁰,< Е =32⁰. Найдите <СКД

3. В равнобедренном треугольнике СДЕ с основанием СЕ и углом Д, равным 102⁰, проведена высота СН. Найдите < ДСН.

Подготавливающие задачи и вопросы имеют большое значение. Рассмотрение некоторой задачи помогает учителю убедить класс в необходимости доказательства теоремы. Иногда решение задачи является частью доказательства. Бывает, что теорема является логическим следствием рассмотренной задачи. Может показаться, что использование подготавливающих задач отнимает много времени. Но одна из главных целей обучения математики – обучение решению задач, а подготавливающая задача – это новая задача и , как правило, нестандартная. Решение этих задач, кроме подготовки к освоению теоремы, еще и развивает мышление, учит поиску решения. Подготавливающие задачи не только облегчают понимание теории, но и позволяют достичь глубокого ее усвоения.

Целесообразно обратить внимание учеников на первые шаги доказательства (сделать чертеж, ввести обозначения, выделить и записать условие и заключение), подчеркнуть их значение. Если все ученики овладевают первыми шагами , то это существенно облегчит доказательство теорем. Многие ученики считают излишним записывать условие требование задачи и начертить чертеж . Нужно их убедить, что не используя условие, нельзя решить задачу или доказать теорему. Требование мы записываем, чтобы видеть цель. Когда не удается решить задачу или доказать теорему нередко причина состоит в том, что не использовано условие или упущена из вида цель.

Пример 12. [24]

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Дано: 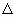АВС

Доказать:

AB2 + AC2 = AB2 + AC2 – 2AB · AC cos 90° = BC2.

. Доказательство:

Без подробной записи доказательства и чертежа учащимся не разобраться в логике исследования данного утверждения. Очень важно приучать учеников слушать себя. Если сразу записать неточную фразу ученика на доске или в его тетради, то он сможет самостоятельно заметить оплошность. Некоторые ученики не делают этого. В результате не приобретают необходимого умения, что сказывается на развитии мышления.

Таким образом, необходимо, чтобы ученик вник в проблему и захотел ее решать. Тогда он будет уточнять постановку задачи, участвовать в поиске решения и получит удовлетворение от работы. При формировании умений делать логические выводы нужно организовать учебно-познавательную деятельность учащихся в такой последовательности::

1. осознание проблемы, т.е. осознание необходимости или пользы изучения нового познавательного вопроса.

2. наблюдение ряда частных случаев, проведение опыта, эксперимента.

3. выказывание догадок, выработка гипотезы.

4. осознание необходимости дедуктивного доказательства.

5. дедуктивное обоснование гипотезы, т.е. доказательство.

6. практические приложения полученного математического результата.

Изучение теоремы можно подразделить на три этапа:

- осознанное усвоение формулировки теоремы;

- обеспечение усвоения доказательства теоремы;

- закрепление теоремы.

В зависимости от характера теоремы , наличия учебного времени на уроке, от уровня развития учащихся, учитель может выбрать один из следующих способов ознакомления школьников с формулировкой теоремы.

1. Учитель подготавливает учащихся к самостоятельному «открытию» теоремы.

Пример 13. [24]

Теорема: У равнобедренного треугольника углы при основании равны. (Тезис)

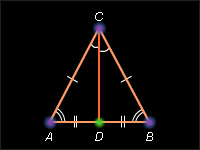
Логическое следствие об углах равнобедренного треугольника можно вывести из известных предпосылок предварительно решая задачу:

Дано: 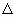АВС - равнобедренный (Аргументы)

АВ- основание

Доказать: < А =< В

Доказательство:( Демонстрация)

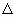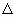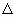Проведем в АВС биссектрису CD угла АCB, рассмотрим АСD и ВСD

АС=СВ - следует(из определения равнобедренного треугольника)

< АСD =< ВСD - следует (из определения биссектрисы угла)

АD –общая сторона

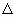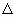АСD = ВСD – следует(из признака равенства треугольников)

< А =< В

2. Учитель организует работу, которая способствует сознательному восприятию и пониманию учащимися новой теоремы, формулировка, которой сообщается им в готовом виде, а доказательство необходимо восстановить по наводящим посылкам.

Пример 14. [24]

Рассмотрим ту же теорему:У равнобедренного треугольника углы при основании равны.

На доске пишется неполные записи условия теоремы и силлогизм.

Учащиеся должны заполнить пробелы.

Дано : 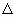АВС равнобедренный с основанием АС

Доказать , что < ____ = <____

Доказательство: Из условия следует ,что ______=_______

Равенство углов можно доказать , если построить ___________треугольники , у которых углы____ и _____ лежат против равных сторон. Такие треугольники получатся , если из вершины равнобедренного треугольника точки ______ провести____________ треугольника АВС . Действительно , 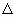____ = ______ так как сторона ______- общая, _____ = _____ , < ____ = <____ . В равных треугольниках _______ и _______ против общей стороны ________ лежат равные углы ____ и ____. Эти углы равны. Теорема доказана.

3. Учитель формулирует теорему сам без предварительной подготовки учащихся, а затем направляет их усилия на ее усвоение. Перед изучением теоремы целесообразно на уроке создать проблемную ситуацию, которая бы мотивировала необходимость ее изучения. С этой целью можно использовать различные практические ситуации и мотивационные упражнения.

Пример15. [29]

Перед изучением признаков равенства треугольников учащиеся знакомятся с определением равных треугольников: «Два треугольника называются равными, если один из них можно наложить на другой так, что они совпадут». Приступая к изучению самих признаков равенства треугольников, следует показать учащимся ограниченность практического применения этого определения (не всегда можно наложить одну треугольную плиту на другую, ввиду их массивности).Отсюда вытекает поиск новых способов определения равных треугольников, на основе исследования, сравнения только некоторых его элементов. Для выявления сознательности усвоения учащимися учебного материала нужна педагогически -целесообразная постановка вопросов. Вопрос считается педагогически целесообразным, если ответ на него не копирует учебник, а будит активную, самостоятельную мысль ученика; такой вопрос должен выявить степень понимания материала. Зачастую безупречная формулировка, воспроизведенная учеником, еще не есть свидетельство полного благополучия. Чтобы узнать, сознательно ли школьники усвоили формулировку теоремы, можно предлагать им искаженные формулировки, а они должны будут найти ошибки.

Пример 16. [29]

После изучения третьего признака равенства треугольников можно задать вопрос учащимся: верно ли , что если периметры двух треугольников равны – равны и сами треугольники?

Учащиеся должны обратить внимание на равенство не соответственных сторон .а периметров , что не является следствием теоремы.

Утверждение неверное.

Контрпример: В треугольниках АВС и МКР периметры равны 26, при этом

АВ=7,ВС=10, АС=9 и МК=6, КР=12, МР=8.

Большое внимание следует уделить закреплению следствий.

Здесь учителю необходимо учитывать два обстоятельства

1. Необходимо сформулировать у всех учащихся навыки доказательства .

2. Учащиеся должны понять и запомнить ее доказательство

Рассмотрим некоторые приемы закрепления выведенного следствия:

Сразу после объяснения новой темы, одному или нескольким учащимся предлагается повторить ее , остальным – слушать. Обычно вызываются учащиеся по желанию, а следовательно, в основном хорошо усваивающие. Этот прием приносит гораздо большую пользу, когда изученное доказательство на этом же уроке повторяют по неполным данным хода исследования, с другими буквенными обозначениями на нем. Такое повторение уже не является столь однообразным, оно требует от учащихся более активной мыслительной деятельности. Следовательно, учащиеся лучше запоминают материал, их внимание более устойчивое.

Пример 17. [24]

Если у треугольников АВС и МКЕ

1) АВ = МК , АС = КЕ и угол А = углу К то АВС=МКЕ

Доказательство:

Равные фигуры__________совместить. Здесь можно совместить либо стороны________ и _______, либо углы_____ и ________. Например, совместим МК и _______ так, чтобы совпали вершины ___ и ___ равных углов. При этом совместятся лучи _____ и ______ (от совместившихся лучей КМ и ____ в данном направлении можно отложить только _______ угол, равный данному углу).

Совместятся вершины __ и ___( от начала совмещенных лучей точки _____ можно отложить только _____ отрезок, равный данному отрезку).

Треугольники АВС __ МКЕ , так как совместились все их____________

Теорема доказана.

1. Перед объяснением новой теоремы учитель предлагает прослушать доказательство и одновременно составить его план. Затем это задание проверяется. Прием очень эффективен, но …. только в тех классах, где предварительно проведена кропотливая работа по формированию умений составлять план.

2. Доказательство рассмотренного утверждения не повторяется на данном уроке. Класс сразу приступает к решению задач по новой теме. Она закрепляется на задачах, решение которых приводят учащихся законченным логическим следствиям.

Пример 18.

(Тезис)

После рассмотрения теоремы: Если два треугольника подобны и отношение их сторон равно k то отношение площадей этих треугольников равно квадрату числа k , целесообразно решить задачу: Площади подобных треугольников F и Q соответственно равны 15 и 60 кв. дм. Одна из сторон треугольника Q равна 1,6 м. Чему равна сходственная ей сторона треугольника F?

(Аргументы)

Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Отношение сходственных сторон равно коэффициенту подобия.

( Демонстрация)

Обозначим буквой а ту сторону треугольникаF, которую надо найти. Тогда 15:60=0,25 =k2, k=0,5 а:1,6м. =0,5 а =0,8 м.

А за 3-5 минут до звонка учитель подводит итог урока. Он предлагает не просто воспроизвести, пересказать изученное на уроке, а задает вопросы, которые заставляют учащихся выделить из нового материала главное, сопоставить с прежними заданиями, сравнить, анализировать, обобщить. И все это увязывается с только что решенными задачами по новой теме.

Пример19.

После урока по теме «Соотношения между сторонами и углами треугольника» целесообразно провести закрепление при решении задачи:

Сравните углы треугольника АВС и выяснить, может ли быть угол А тупым, если АВ больше ВС больше АС.

При решении необходимо выделить из условия задачи главное, сопоставить с известными посылками , сравнить, анализировать, обобщить.

(известные посылки к задаче )

а) против большей стороны в треугольнике лежит больший угол;

б) сумма углов треугольника равна 180 градусов;

в) в треугольнике не может быть два тупых угла. (постановка проблемы). Сравнить углы треугольника АВС.(выдвижение гипотезы). Может ли быть угол А тупым, если АВ больше ВС больше АС. ( проверка гипотезы).Если угол А тупой, то в треугольнике АВС два тупых угла (доказательство или опровержение гипотезы).

Таким образом, при такой форме подведения итогов урока у учащихся формируется умение исследовать, делать аргументированные выводы из имеющихся предпосылок; новый материал запоминается эффективнее, так как он повторяется сразу после момента наиболее интенсивного забывания, а мыслительная деятельность учащихся разнообразна и активна .