ГЛАВА 2. Формирование умения выводить логические следствия из данных предпосылок при изучении темы «Треугольник» исследовательским методом

Организация исследовательской деятельности при обучении геометрии в основной и старшей школе

Основным методом всех технологий развивающего обучения является исследовательская деятельность учащихся.

В научно-методической литературе методы исследования называют также метод открытий, эвристическим методом и методом решения проблем.

И сегодня очень актуально звучат слова В.П. Вахтерова о том, что образован не тот, кто много знает, а тот, кто хочет много знать, и умеет добывать эти знания. Он подчеркивал исключительную важность мыслительных умений школьников - умения анализировать, сравнивать, комбинировать, обобщать и делать выводы; важность умения пользоваться приемами научного исследования, хотя бы и в самой элементарной форме.

Исследовательская деятельность учащихся – это совокупность действий поискового характера, ведущая к открытию неизвестных для учащихся фактов, теоретических знаний и способов деятельности.

В качестве основного средства организации исследовательской работы выступает система исследовательских заданий.

Исследовательские задания – это предъявляемые учащимися задания, содержащие проблему; решение ее требует проведения теоретического анализа, с помощью которых учащиеся открывают ранее неизвестное для них знание.

Цель исследовательского метода – «вызвать» в уме ученика тот самый мыслительный процесс, который переживает изобретатель данного открытия или изобретения. Школьник должен почувствовать прелесть открытия.

Таким образом, исследовательский процесс – это не только логико- мыслительное, он и чувственно-эмоциональное освоение знаний.

Основные этапы учебного исследования

1 Мотивация исследовательской деятельности

2 Формулирование проблемы

3 Сбор, систематизация и анализ фактического материала

4 Выдвижение гипотез

5 Проверка гипотез

6 Доказательство или опровержение гипотез

1) Мотивация – очень важный этап процесса обучения, если мы хотим, чтобы оно было творческим. Целью мотивации, как этапа урока, является создание условий для возникновения у ученика вопроса или проблемы.

2) Этап формулирования проблемы – самый тонкий и «творческий» компонент мыслительного процесса. В идеале сформулировать проблему должен сам ученик в результате решения мотивирующей задачи. Однако в реальной школьной практике такое случается далеко не всегда: для очень многих школьников самостоятельное определение проблемы затруднено; предлагаемые ими формулировки могут оказаться неправильными. А поэтому необходим контроль со стороны учителя.

3) Сбор фактического материала может осуществляться посредством проведения испытаний, всевозможных проб, измерения частей фигуры, каких-либо параметров и т.д. Пробы (испытания) не должны быть хаотичными, лишенными какой-либо логики. Необходимо задать их направление посредством пояснений, чертежей и т.п.

Систематизацию и анализ полученного материала удобно осуществлять с помощью таблиц, схем, графиков и т.п. – они позволяют визуально определить необходимые связи, свойства, соотношения, закономерности.

4) Выдвижение гипотез. Полезно прививать учащимся стремление записывать гипотезы на математическом языке, что придает высказываниям точность и лаконичность. Не нужно ограничивать число предлагаемых учащимися гипотез.

5) Проверка гипотез позволяет укрепить веру или усомниться в истинности предложений, а может внести изменения в их формулировки. Расхождение результатов служит основанием для отклонения гипотезы или уточнения

условий ее справедливости.

6) На последнем этапе происходит доказательство истинности гипотез, получивших ранее подтверждение; ложность же их может быть определена с помощью контрпримеров. Поиск необходимых доказательств часто представляет большую трудность, поэтому учителю важно предусмотреть всевозможные подсказки.

Пример 8

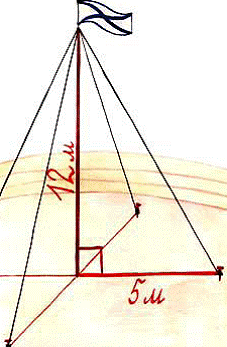
В качестве иллюстрации учебного исследования можно привести фрагмент урока геометрии по теме «Теорема Пифагора».Мотивирующей (исходной) задачей может служить следующая задача: «Для крепления мачты нужно установить 4 троса. Один конецкаждого троса должен крепитьсяна высоте 12 м, другой на земле нарасстоянии 5 м от мачты. Хватитли 50 м троса для крепления мачты?»

Анализируя математическую модель этой практической задачи, учащиеся формулируют проблему – нужно найти гипотенузу прямоугольного треугольника по двум известным катетам.

Для решения этой проблемы можно организовать практическую работу исследовательского характера, предложив учащимся задание по рядам: построить прямоугольные треугольники с катетами 12 и 5; 6 и 8; 8 и 15 см и измерить гипотенузу. Результаты заносятся в таблицу.

а12 6 8

b5 8 15

с13 10 17

Затем учащимся предлагается выразить формулой зависимость между длинами катетов и гипотенузой в прямоугольных треугольниках. Школьники выдвигают свои гипотезы, которые обсуждаются.

После установления зависимости между сторонами прямоугольного треугольника эмпирический вывод требует теоретического обоснования, т.е. доказывается теорема Пифагора.

В качестве домашнего задания по этой теме можно предложить

исследовательскую работу со следующей мотивирующей задачей:

«Кто же на самом деле открыл теорему Пифагор? Почему она долгое время называлась «теоремой невесты»? Существуют ли другие доказательства теоремы?»

Цель этой исследовательской работы – научить учеников использовать дополнительную литературу, применять Интернет в собственной

образовательной деятельности.

Несколько примеров мотивирующих задач.

Пример 9 [24]

При изучении темы «Сумма внутренних углов треугольника»в качестве исходного задания можно предложить такую задачу: «Построить треугольник по трем заданным углам:

1) . А = 90о, . В = 60о, . С = 45о;

2) . А = 70о, . В = 30о, . С = 50о;

3) . А = 50о, . В = 60о, . С = 70о».

Учащиеся, вооружившись линейкой и транспортиром, начинают строить треугольники. В первом случае, построив углы А и В и отложив угол в 45о от луча АС (или ВС, кому как нравится), ребята увидят, что вместо треугольника получается четырехугольник. Во втором случае независимо от того, какие первые два угла школьники выбирают для построения, всегда получается треугольник, третий угол которого больше, либо меньше заданного. И только в третьем случае выстраивается треугольник по трем заданным углам.

По окончании уже можно выдвинуть предположение о сумме углов треугольника. Здесь уместен провокационный вопрос:«В каком треугольнике, по вашему мнению, сумма внутренних углов больше, в остроугольном или тупоугольном?» Практика показывает, что почти в каждом классе найдутся несколько человек, которые, зная, что тупой угол всегда больше острого, по аналогии скажут, что сумма внутренних углов тупоугольного треугольника больше, чем остроугольного. Далее им предлагается на практике проверить свое утверждение.

Математика дает широкое поле для исследования. Изучая математику, учащиеся кратко повторяют путь человечества, который оно прошло, добывая математические знания.

Пример 10 [24]

Рассматриваем многогранники. Учащиеся могут самостоятельно прийти к соотношению между числом вершин, граней и ребер для любого выпуклого многогранника, которое выражается известной формулой Эйлера.

Для эксперимента учащимся предлагаются модели различных выпуклых многогранников, используя которые, они заполняют таблицу.