Взаимное расположение точки и линии

Точка в пространстве по отношению к линии может занимать два положения: принадлежать ей или не принадлежать. Если она принадлежит линии, она составляет с ней единое целое и проекции ее на чертеже лежат на соответствующих проекциях линии, а также на одной линии связи.

Если же хотя бы одна из проекций точки не лежит на проекции линии, точка ей не принадлежит. На рисунке 83 показан комплексный чертеж линии l, а также ряда точек. Из чертежа видно, что точка А принадлежит линии b, так как горизонтальная ее проекция А₁ лежит на горизонтальной проекции линии 1₁, а фронтальная проекция точки А₂ расположена на фронтальной проекции прямой А и лежит на одной вертикальной линии связи с точкой А₁. Точки В и С не принадлежат линии l, так как в первой фронтальная, а во второй горизонтальная проекции не принадлежат соответствующим проекциям линии. Точки D и Е не принадлежат линии l, так как ни одна из их проекций не принадлежит соответствующей проекции линии.

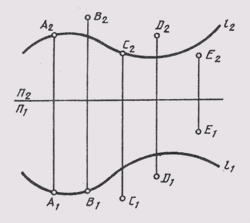
Рисунок 83 – Комплексный чертеж линии

Вопросы для самоконтроля

1 Как образуется кривая линия?

2 Как образуется двухпроекционный чертеж прямой линии?

3 Какая прямая называется прямой общего положения?

4 Какие лучи называются проецирующими?

5 Как определяется натуральная величина отрезка прямой линии?

6 Что называется шагом винтовой линии?

Поверхности

Образование поверхностей

Поверхностью называют множество последовательных положений линий, перемещающихся в пространстве. Эта линия может быть прямой или кривой и называется образующейповерхности. Если образующая кривая, она может иметь постоянный или переменный вид. Перемещается образующая по направляющим,представляющим собой линии иного направления, чем образующие. Направляющие линии задают закон перемещения образующим. При перемещении образующей по направляющим создается каркасповерхности (рисунок 84), представляющий собой совокупность нескольких последовательных положений образующих и направляющих. Рассматривая каркас, можно убедиться, что образующие l и направляющие т можно поменять местами, но при этом поверхность получается одна и та же.

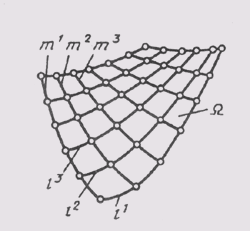
Рисунок 84 – Образующая поверхность

Любую поверхность можно получить различными способами. Так, прямой круговой цилиндр (рисунок 85) можно создать вращением образующей l вокруг оси г, ей параллельной. Тот же цилиндр образуется перемещением окружности т с центром в точке О, скользящим по оси i. Любая кривая k, лежащая на поверхности цилиндра, образует эту поверхность при своем вращении вокруг оси /'.

На практике из всех возможных способов образования поверхности выбирают наиболее простой.

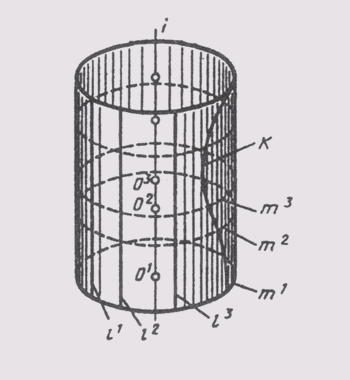
Рисунок 85 – Прямой круговой цилиндр

В зависимости от формы образующей все поверхности можно разделить на линейчатые,у которых образующая прямая линия, и нелинейчатые,у которых образующая кривая линия.

В линейчатых поверхностях выделяют поверхности развертывающиеся, совмещаемые всеми своими точками с плоскостью без разрывов и складок, и неразвертывающиеся, которые нельзя совместить с плоскостью без разрывов и складок.

К развертывающимся поверхностям относятся поверхности всех многогранников, цилиндрические, конические и торсовые поверхности. Все остальные поверхности — неразвертывающиеся. Нелинейчатые поверхности могут быть с образующей постоянной формы (поверхности вращения и трубчатые поверхности) и с образующей переменной формы (каналовые и каркасные поверхности).

Для задания поверхностей выбирают такую совокупность независимых геометрических условий, которая однозначно определяет данную поверхность в пространстве. Эта совокупность условий называется определителем поверхности. Определитель состоит из двух частей: геометрической, в которую входят основные геометрические элементы и соотношения между ними, и алгоритмической, содержащей последовательность и характер операций перехода от основных постоянных элементов и величин к переменным элементам поверхности, т. е. закон построения отдельных точек и линий данной поверхности. Поверхность на комплексном чертеже задается проекциями геометрической части ее определителя с указанием способа построения ее образующих. На чертеже поверхности для любой точки пространства однозначно решается вопрос о принадлежности ее данной поверхности. Графическое задание элементов определителя поверхности обеспечивает обратимость чертежа, но не делает его наглядным. Для наглядности прибегают к построению проекций достаточно плотного каркаса образующих и к построению очерковых линий поверхности (рисунок 86). При проецировании поверхности Q на плоскость проекций проецирующие лучи прикасаются к этой поверхности в точках, образующих на ней некоторую линию l, которая называется контурнойлинией. Проекция контурной линии называется очеркомповерхности. На комплексном чертеже любая поверхность имеет: на П₁— горизонтальный очерк, на П₂ — фронтальный очерк, на П₃ — профильный очерк поверхности. Очерк включает в себя, кроме проекций линии контура, также проекции линий обреза.

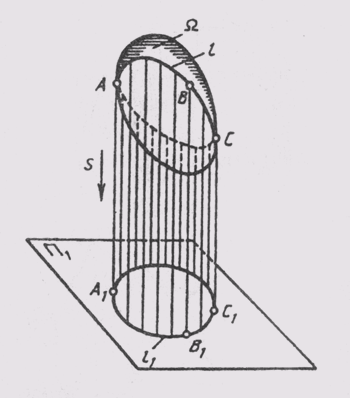
Рисунок 86 – Построение очерковых линий поверхности

Из существенного множества поверхностей в курсе инженерной графики будут рассмотрены все развертывающиеся поверхности, к которым относятся гранные, конические, цилиндрические, торсовые поверхности, некоторые поверхности вращения и винтовые.

Простейшей поверхностью, широко используемой в инженерной графике, является плоскость, представляющая собой поверхность, образованную перемещением прямолинейной образующей (рисунок 87) по двум параллельным или пересекающимся прямым m₁и m₂.

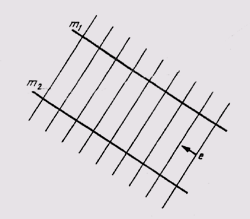
Рисунок 87 – Образование плоскости