Указания к решению задачи 9.

На листе бумаги ватмана формата А3 (297х420 мм) строят развертки поверхностей.

Развертка цилиндра вращения. Выбирают горизонтальную прямую линию и на ней спрямляют линию нормального сечения цилиндра вращения - окружность радиуса R₁. Строят развертку боковой поверхности цилиндра. На развертке помечают прямолинейные образующие, проходящие через характерные точки пересечения цилиндра с конусом. Эти точки отмечают на соответствующих образующих. Они определяют линию пересечения поверхностей развертки. Полная развертка цилиндра вращения представляется разверткой его боковой поверхности и основаниями - окружностями радиуса R₁.

Развертка конуса вращения. Разверткой поверхности конуса вращения является круговой сектор с углом

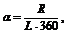
где R - радиус окружности основания конуса вращения;

L - длина образующей.

На развертке конуса вращения строят прямолинейные образующие или параллели, проходящие через характерные точки линий пересечения конуса вращения с цилиндром вращения. Через такие точки проходят линии пересечения поверхностей в преобразовании (на развертке). Контур боковой поверхности конуса вращения и его основания (окружности) обвести основной линией чертежа.

Кальку и листы писчей бумаги с планом решения задачи 9 наклеить с левого края листа 6.

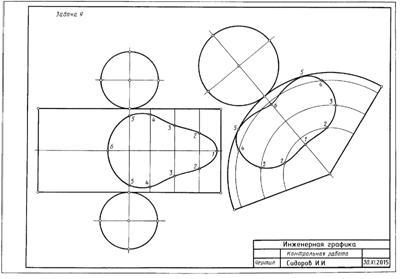
Рис 6

Задачи, рекомендуемые для подготовки к экзамену

Целью решения данных задач является закрепление, изучаемого материала, связь их с практическими примерами.

Проекция точки

Вопросы для самоконтроля

1. Что называется центральной проекцией точки? Что называется проекцией? Что называется ортогональной проекцией?

2. Какой чертёж называют «обратимым»?

3. На сколько плоскостей проекций необходимо проецировать объекты, чтобы получить «обратимый» чертёж? Как эти плоскости называются и как они располагаются?

4. Что называется двухкартинным комплексным чертежом?

5. Что называют осью проекций? Какие прямые называют «линиями связи»?

6. Как называются проекции точки на плоскостях П₁, П₂ , П₃ ?

7. Что называется высотой точки? Что называется глубиной точки? Что называется широтой точки?

8. Как восстановить положение точки в пространстве по её проекциям?

9. Что называется определителем точки и как он записывается?

1. По наглядному изображению построить комплексный чертеж точек А, В, С (рис. 1).

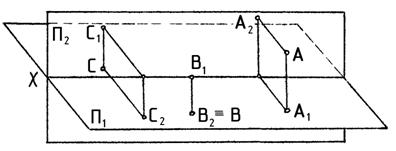
Рис.1

2. По двум проекциям точек А, В, С, D построить третьи проекции и их наглядное изображение (рис. 2).

Рис. 2

3. Дан параллелепипед с точкой А внутри. Построить:

а) точку В, симметричную точке А относительно верхней грани параллелепипеда;

б) точку С , симметричную точке А относительно передней грани;

в) точку D , симметричную точке А относительно правого верхнего ребра;

г) точку Е , симметричную точке А относительно верхнего переднего ребра;

д) точку F, симметричную точке А относительно нижней передней правой вершины (рис.3).

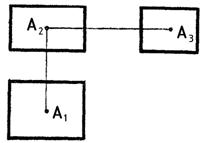
Рис. 3

Прямая, её проекции и следы

Вопросы для самоконтроля

1. Как можно задать прямую на комплексном чертеже?

2. Какие прямые называются прямыми общего положения, а какие прямыми частного положения? Как располагаются их проекции?

3. Что называется следом прямой?

4. В каком случае точка принадлежит прямой?

1. Построить комплексный чертеж и наглядное изображение прямой общего положения АВ в системе трех плоскостей А (38,10,38); В (5,42,5).

2. Определить натуральную величину отрезка АВ и углы наклона его к горизонтальной и фронтальной плоскостям проекций (рис. 4)

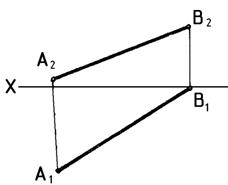
Рис. 4

3. Построить горизонтальные и фронтальные следы М и N прямой АB . Указать, через какие четверти прямая проходит, и отметить ее видимую часть (рис. 5).

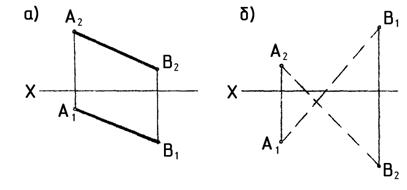
Рис. 5

Взаимное положение прямых

Вопросы для самоконтроля

1. Какое взаимное положение могут занимать две прямые?

2. Как изображаются на комплексном чертеже пересекающиеся, параллельные и скрещивающиеся прямые линии?

3. Что называют «конкурирующими точками»? Как определяется их «видимость» на комплексном чертеже?

4. В каком случае прямой угол проецируется на плоскость проекций без искажения?

1. Через точку А провести прямую, пересекающую данную прямую ВС в точке F, отстоящей от фронтальной плоскости проекций на 15 мм (рис.6).

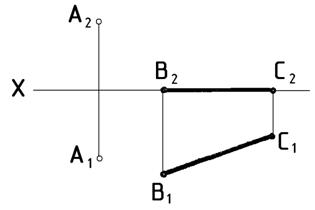
Рис. 6

2. Пересечь прямые АВ и СD прямой ЕК , проходящей через точку M (рис.7).

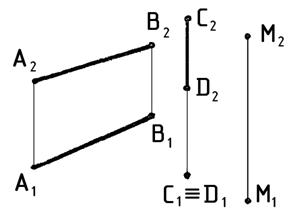
Рис. 7

3. Построить проекции квадрата ABCD по заданной стороне АВ и направлению горизонтальной проекции его смежной стороны m (рис.8).

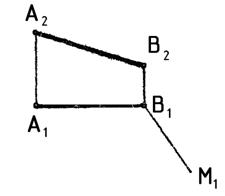
Рис. 8