Взаимное пересечение многогранников

Многогранные поверхности пересекаются друг с другом по замкнутымломанымлиниям,дляпостроениякоторыхсначаланаходимточки пересеченияреберодногомногогранникасгранямидругого,азатем– ребервторогосгранямипервого.Соединяявопределеннойпоследовательностиполученныеточки,строимискомуюломаную,каждоезвено которойпредставляетсобойпрямуюпересечениядвухграней–грани первого многогранника с гранью второго.

Итак, построение линии пересечения двух многогранников сводится к решению задачи на пересечение прямой линии с многогранником (или на взаимное пересечение двух плоскостей – граней многогранников).

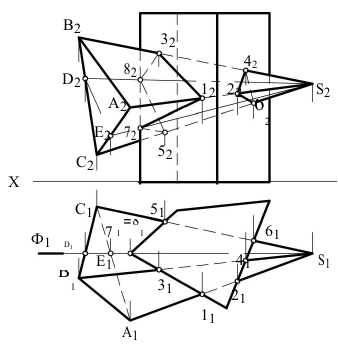
На рисунке 78 приведен пример построения линии взаимного пересечения прямой четырехугольной призмы с пирамидой SABC.

Рисунок 78 – Пересечение прямой четырехгранной призмы с пирамидой SABC

ОснованиепризмысовмещеносплоскостьюП₁.Горизонтальные проекции вертикальных ребер преобразуются в точки. Грани боковой поверхности призмы представляют собой отсеки горизонтально-проецирующихплоскостей.Линияпересечениямногогранниковопределяетсяпо точкам пересечения ребер каждого из них с гранями другого многогранника. Так, ребро SA (S₁A₁, S₂A₂) пирамиды пересекает две вертикальные грани призмы: одну в точке 1(1₁1₂), вторую – в точке 2 (2₁ 2₂). Ребро SB (S₁B₁, S₂B₂) пирамиды пересекает две вертикальные грани призмы в точках 3(3₁ 3₂) и 4(4₁ 4₂); ребро SC (S₁C₁, S₂C₂) – в точках 5(5₁ 5₂) и 6 (6₁ 6₂).

Из четырех вертикальных ребер призмы только одно пересекает пирамиду.Находимточкиегопересечениясгранямипирамиды.Черезэто ребро и вершину S (S₁, S₂) пирамиды проводим вспомогательную горизонтально-проецирующую плоскость Ф. Она пересекает пирамиду по прямымDS (D₁S₁, D₂S₂) иES (E₁S₁, E₂S₂). Эти прямые пересекают ребро призмы в точках 7(7₁ 7₂) и 8(8₁ 8₂) – в точках пересечения ребра призмы с гранями пирамиды. Соединяя каждые пары таких точек одних и тех же граней отрезками прямых, получаем две линии пересечения многогранников. Одна из них представляет собой пространственный многоугольник 138571(1₁3₁8₁5₁7₁1₁, 1₂3₂8₂5₂7₂1₂), другая – треугольник 246(2₁4₁6₁, 2₂4₂6₂).

Видимыми являются только те из отрезков многоугольников пересечения, которые принадлежат видимым граням многогранников; невидимые отрезки обозначаем на эпюре штриховыми линиями.

Отрезки 24(2₁4₁, 2₂4₂) и 26(2₁6₁, 2₂6₂) линии пересечения 246(2₁4₁6₁, 2₂4₂6₂) видимы на фронтальной проекции. Они принадлежат видимым гранямпризмыипирамиды.Отрезок46(4₁6₁,4₂6₂)являетсяневидимымна фронтальнойпроекции.Этототрезокпринадлежитвидимойнаэтойпроекциигранипризмыиневидимойгранипирамиды.Нафронтальнойпроекции видимы отрезки 13(1₁3₁, 1₂3₂) и 17(1₁7₁, 1₂7₂) второй линии пересечения, а отрезки 38(3₁8₁, 3₂8₂), 85(8₁5₁, 8₂5₂) и 75(7₁5₁, 7₂5₂) этой линии невидимы.

Поверхности вращения. Примеры поверхностей вращения

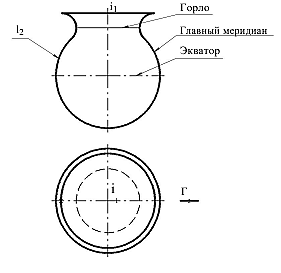
В числе кривых поверхностей – линейчатых и нелинейчатых – имеютсяширокораспространенныевпрактикеповерхностивращения.Поверхностью вращения называютповерхность,полученнуюотвращения какой-либо образующей линии l вокруг неподвижной прямой i– оси поверхности (рисунок 79).

Рисунок 79 – Поверхность вращения

При вращении вокруг оси каждая точка образующей l описывает окружность, которую называют параллелью поверхности вращения. Плоскости параллелей перпендикулярны оси поверхности. Наибольшую из параллелей поверхностивращенияназываютэкваторомповерхности,анаименьшую – горлом (шейкой).

Линии, получаемые при пересечении поверхности вращения плоскостями, проходящими через ось, называют меридианами поверхности. Меридиан, расположенный во фронтальной плоскости Г, называется главным меридианом.

Различаютповерхностивращенияспрямолинейнойикриволинейной образующей.

К поверхностям вращения с прямолинейной образующей относятся цилиндрическая и коническая поверхности вращения.

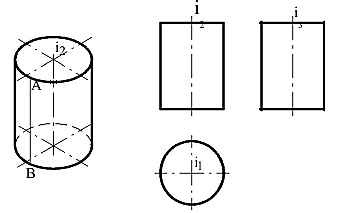
Цилиндрическойповерхностьювращенияназываетсяповерхность, образованнаяпрямойлинией(образующей),которая перемещается, оставаясь параллельной оси вращения. Боковая поверхность прямого кругового цилиндра (рисунок 80) образована движением отрезка АВ вокруг вертикальной оси i.

Рисунок 80 – Цилиндрическая поверхность вращения

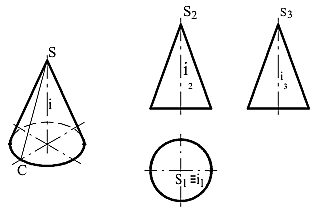
Коническая поверхность вращения представляет собой поверхность, образующая прямая которой пересекает ось вращения в точке, называемой вершинойконуса.Боковаяповерхностьпрямого кругового конуса (рисунок 81) образованавращениемобразующейSCвокругосиконусапо направляющей – окружности.

Рисунок 81 – Коническая поверхность вращения

Сферой называется поверхность, образованная вращением окружности вокруг одного из ее диаметров. На все плоскости проекций сфера проецируется в круг с радиусом, равным радиусу сферы (рисунок 82).

Эллипсоидом вращения называется поверхность, образованная вращением эллипса вокруг одной из его осей.

Рисунок 82 – Сфера

Параболоид вращения образуется вращением параболы вокруг ее оси.Однополостной гиперболоид вращения образуется при вращении гиперболы вокруг ее мнимой оси, а двухполостной – при вращении вокруг действительной оси.

Тором называется поверхность, образованная вращением вокруг оси, лежащей в плоскостиэтой окружности и не проходящей через ее центр. Тор относится к поверхностям вращения четвертого порядка.

Винтовой называется поверхность, которая описывается какой-либо линией (образующей) при ее винтовом движении.

Винтовое движение линии характеризуется ее вращением вокруг определенной оси i и поступательным перемещением, параллельным оси i.

Винтовыеповерхностисобразующимипрямымилинияминазываютгеликоидами.

Геликоид называют прямым или наклонным в зависимости от того, перпендикулярна образующая линия оси геликоида или нет.

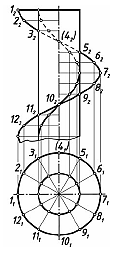
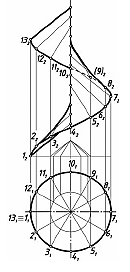
На рисунке 83 изображен прямой геликоид, а на рисунке 84 – наклонный геликоид.

Рисунок 83 – Прямой геликоид Рисунок 84 – Наклонный геликоид