Введение в предмет начертательная геометрия
Начертательная геометрия возникла в глубокой древности. Потребность в изображениях пространственных форм на плоскости, развитие изобразительного искусства, техники предопределили появление начертательной геометрии.
Ученые всего мира внесли большой вклад в развитие методов построения изображений пространственных форм на плоскости. Это великий греческий геометр Эвклид (III в. до н.э.), римский архитектор Витрувий (I в. до н.э.).
Значительные труды по методам изображений были написаны в эпоху Возрождения: итальянскими архитекторами Леоном Батиста Альберти (1404 – 1472 гг.), Леонардо да Винчи (1455 – 1519 гг.), немецким живописцем и архитектором Альбрехтом Дюрером (1471 – 1528 гг.).
Математическую трактовку перспективы дал итальянский ученый Гвидо Убальди (1545 – 1607 гг.), а французский архитектор Жерар Дезарг (1593 – 1662 гг.) в своем труде заложил теоретический фундамент перспективы.
В России практические приемы построения графических изображений были известны еще в давние времена. Рисунки домов, крепостей в различных древних летописях сохранили для нас достаточно совершенные для своего времени примеры изображений.
Работы таких великих русских мастеров, как иконописец Рублев, механик-самоучка И.П. Кулибин, зодчие Д.В. Ухтомский, В.И. Баженов, М.Ф. Казаков и многие другие, являются образцами правильных проекционных изображений.
Таким образом, методы построения графических изображений постоянно развивались в различных странах независимо друг от друга, но только французский инженер и ученый Гаспар Монж (1746 – 1818 гг.) смог сформулировать главные элементы теории построения графических изображений, используя прямоугольное проецирование на две взаимно перпендикулярные плоскости.
В 1798 году Гаспар Монж опубликовал свой главный научный труд «Начертательная геометрия».
В России курс начертательной геометрии впервые стал изучаться в 1810 году. Первым русским профессором начертательной геометрии и крупным ученым в этой области стал Я.А. Севастьянов (1796 – 1849 гг.).
Значительный вклад в развитие начертательной геометрии внесли русские ученые: Н.И. Макаров, В.И. Курдюмов, Н.А. Рынин, А.И. Добряков, Н.Ф. Четверухин и многие другие.
Позднее продолжили свои исследования такие ученые, как В.О. Гордон, С.А. Фролов, А.В. Бубенников, Н.Н. Крылов и др.
Метод проецирования. Центральное и параллельное проецирование. Основные свойства.Прямоугольное (ортогональное) проецирование
Для отображения геометрической фигуры на чертеже применяют операцию проецирования. Она заключается в том, чточерезточку пространствапроводятпроецирующуюпрямуюдопересеченияс плоскостьюпроекций.Точкупересеченияпроецирующейпрямойс плоскостьюпроекцийназываютпроекциейданнойточкинаданную плоскость проекций.
Различаютследующиеметодыпроецирования:центральное, параллельное (косоугольноеиортогональное),перспективное, аксонометрическое и др.
Центральноеиперспективноепроецированиенашлоширокое применениевархитектуреистроительстве,ортогональное (прямоугольное) и аксонометрическое – в машино- и приборостроении.
Чертежи,построенныепометодупроецирования,называются проекционными.
Центральное проецирование
Пусть в пространстве задана плоскость α, которую будем называть плоскостью проекций.
Выберем какую-либо точку S, не лежащую на плоскости проекций. Эту точку будем называть центром проецирования.
Заданные точки А, В, С пространства будем проецировать на плоскость проекций α. Для этого через точки А, В, С из центра проекций S проведем прямые. Эти прямые будет называться проецирующей прямой. Затем находим точку пересечения А1, В1,С1проецирующей прямой SA,SB, SC с плоскостью проекций α. Точка А1, В1,С1 будет называться проекцией точек А, В, С (рисунок 1).
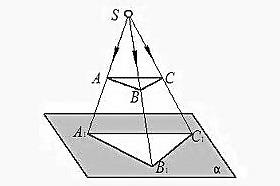
Рисунок 1 – Центральное проецирование
Очевидно, что каждой точке пространства будет однозначно соответствовать своя собственная проекция. Однако на рисунке 2 мы видим, что проекцией точки А и точки В является точка пересечения их общей проецирующей прямой с плоскостью проекций.
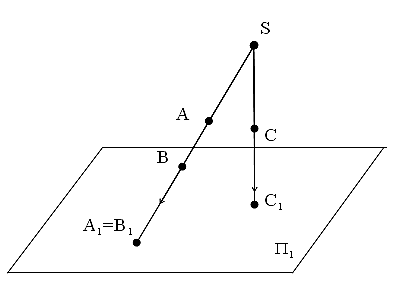
Рисунок 2 – Центральное проецирование
Следовательно, такое изображение не является взаимно однозначным, и судить о положении точек А и Вв пространстве по одной проекции нельзя, потому что одним из требований, предъявляемых к чертежам, является точное определение положения пространственного объекта по его изображению, по его проекциям.
Параллельное проецирование
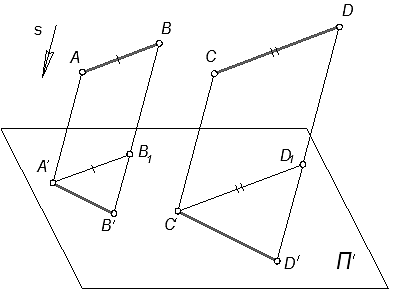
Если центр проецирования S∞ удален в бесконечность (рисунок 3), то проецирующие лучи станут параллельны друг другу. Такое проецирование называется параллельным.
Рисунок 3 – Параллельное проецирование
Проецирующие лучи, исходящие из бесконечного далека, могут быть наклонены под любым углом к плоскости проекций.
При заданном аппарате проецирования можно построить параллельную проекцию любой точки пространства. Для этого через заданные точки А и В проведем проецирующие прямые, параллельную направлению s, и найдем точки А1, В1 – точки пересечения этой прямой с плоскостью проекций П1.
Через точки А и В параллельно заданному направлению в пространстве можно провести только одну прямую, следовательно, каждая точка пространства имеет одну и только одну параллельную проекцию.
Точки А и В принадлежат одному и тому же проецирующему лучу, параллельному направлению s. Поэтому проекции этих точек В1 и А1 совпадают. Отсюда следует, что по одной заданной проекции положение в пространстве точек В и А определить невозможно.
