Данные к задаче 8 (размеры и координаты, мм)

№	xK	yK	zK	R	h	xE	yE	zE	r
12,28
15,29
18,30

Задача 9(Тема 8,9) По двум проекциям модели построить третью проекцию и изометрию. Построить линии среза на проекциях модели. Найти натуральную величину среза и построить её на аксонометрической проекции. Данные для своего варианта взять согласно рисунку 4. Пример выполнения листа дан на рисунке 3.

Методические рекомендации к решению задачи 9.

В практике конструирования нередко возникает необходимость построения натурального вида наклонного сечения детали проецирующей плоскостью или, как его называют «наклонного сечения». Натуральный вид наклонного сечения может быть построен различными способами начертательной геометрии - вращением, плоскопараллельным перемещением, совмещением и переменой плоскостей проекций. Наиболее рациональным следует считать способ замены плоскостей проекций.

Напомним кратко сущность этого способа. При пересечении прямоугольной призмы фронтально проецирующей плоскостью (рис.1) сечение проецируется на фронтальную плоскость в виде отрезка прямой, совпадающей со следом Pν а на горизонтальную плоскость - в виде прямоугольника у которого стороны 1-2 и 3-4 искажены. Для определения натуральной величины сечения, плоскость H заменяем на новую плоскость Q, проведённую перпендикулярно плоскости V и параллельно плоскости сечения P. Новая плоскость X₁ параллельна следу Pν , а новые линии связи перпендикулярны новой оси X₁ . Расстояния проекций точек 1,2,3 и 4 на новой плоскости Q от оси X₁ (a и b) равно расстояниям проекций этих же точек на заменённой плоскости H от оси X. Соединив полученные точки 1,2,3 и 4 на плоскости X, получаем натуральную величину сечения призмы плоскостью P.

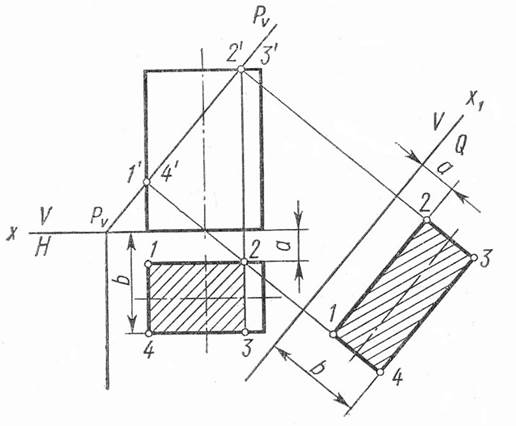
Рис.1 Построение натуральной величины наклонного сечения прямоугольной призмы фронтально проецирующей плоскостью.

При недостатке места на чертеже, для расположения сечения в соответствии с непосредственной проекционной связью, его можно смещать, как показано на рисунке 2. При этом линии связи, перпендикулярные следу секущей плоскости, прерываются и в том же порядке наносятся на новом месте. В остальном построение аналогично предыдущему. Следует отметить лишь, что в примере, приведённом на рис.2 часть детали представляет собой конус, при пересечении которого плоскостью А получается эллипс. Большая ось эллипса 1-2 определяется на фронтальной проекции по точкам (1' и 2') пересечения секущей плоскости с очерковыми образующими конуса. Определение малой оси эллипса ведём следующим образом: через середину большой оси О проводим вспомогательную секущую плоскость Q, перпендикулярную оси конуса, она пересекает конус по окружности радиуса R, а плоскость А – по горизонтали перпендикулярной плоскости V.

Точки 3 и 4 пересечения этих линий (см. горизонтальную проекцию) определяют величину малой оси эллипса, которую отмеряем по направлению малой оси на натуральном виде сечения. Аналогично определяются и промежуточные точки эллипса. На рис.2 показано определение промежуточных точек 5 и 6.Через произвольно выбранную фронтальную проекцию точки 5 – точку 5' проведена вспомогательная плоскость S, горизонтальные проекции двух симметричных точек 5 и 6 определяются в пересечении двух линий сечения плюс плоскостью S - окружности (на конусе) и горизонтали (на плоскости А). На натуральном виде сечения расстояние 5-6 отмечено на соответствующей линии связи.

Наглядное изображение детали рекомендуется выполнить в изометрической проекции с увеличенными коэффициентами искажения, т.е. в масштабе 1,22:1.

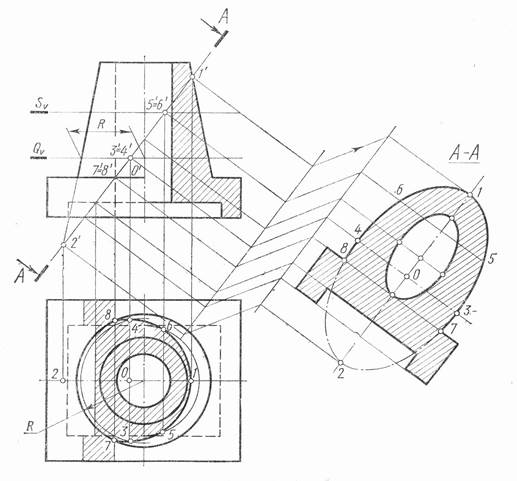
Рис.2 Построение наклонного сечения сложной геометрической фигуры со смещением натурального вида фигуры сечения

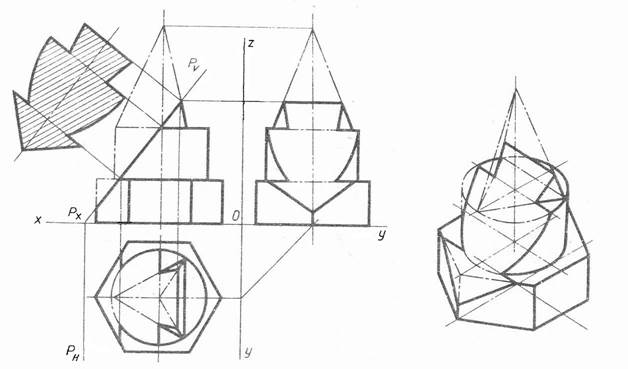
Рис.3 Пример выполнения задачи 9.

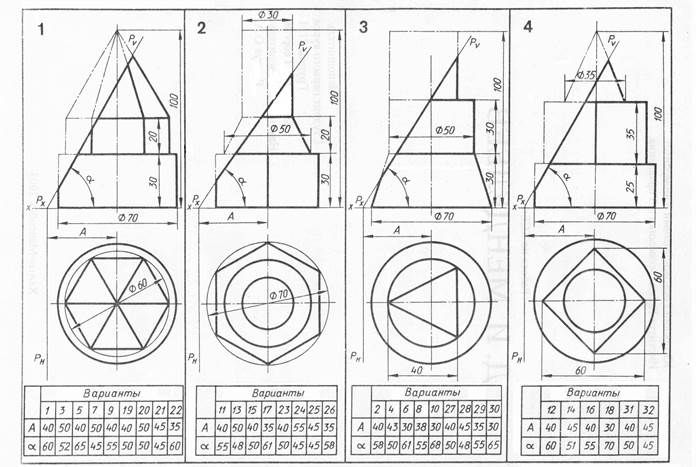
Рис. 4 Данные задаче 9 для построения наклонного сечения

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Гордон В.О. Курс начертательной геометрии. Учебное пособие для ВУЗов. М.: Высш. шк., - 2003.

2. Гордон В.О. Курс начертательной геометрии. Учебное пособие для ВУЗов. М.: Высш. шк., - 2002 .

6. Локтев О.В. Краткий курс начертательной геометрии. Уч. для ВТУЗов., М.: Высш. шк., - 2001.

7. Начерт. геом. Уч. для ВУЗов./Под ред. Крылова Н.Н.,

М., Высш. школа, - 2002.

12. Чекмарев А.А. Начерт. геом. и черчение. Уч. для

ВУЗов. М., Гуманитар. изд. центр «ВЛАДОС», - 2001.

13. Гордон В.О. Сборник задач по курсу начертательной геометрии. Учебное пособие для ВТУЗов. М., Высш. шк.,

- 2003.

14. Гордон В.О. Сборник задач по курсу начертательной геометрии. Учебное пособ. для ВТУЗов. М., Высш. шк., - - 2002.

15. Короев Ю.И. Сборник задач и заданий по начертательной геометрии. Учебное пособие для ВУЗов. М., Архитектура, - 2003.

16. Локтев О.В. Задачник по начертательной геометрии. Учебное пособие для ВТУЗов. М., Высш. шк., - 2002.

17. Пеклич В.А. Задачи по начертательной геометрии.

Учебное пособие для ВТУЗов. М., Высш. шк., - 1999. 1