Тест № 2 «Поверхности. Развертки»

1.На чертеже задан прямой круговой конус. Чем является отрезок SВ?

1 – образующей 2 - осью вращения

3 – направляющей 4 - основанием

2 Как называются очерковый сферы?

1 а – нулевой меридиан; в – главная широта; с – профильный меридиан.

2 а – главный меридиан; в – экватор; с - профильный меридиан.

3 а - главный меридиан; в – экватор; с - дополнительный меридиан.

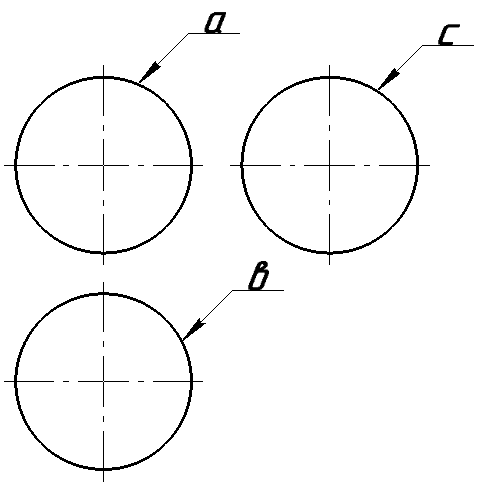
3. На каком чертеже заданная поверхность не является поверхностью вращения?

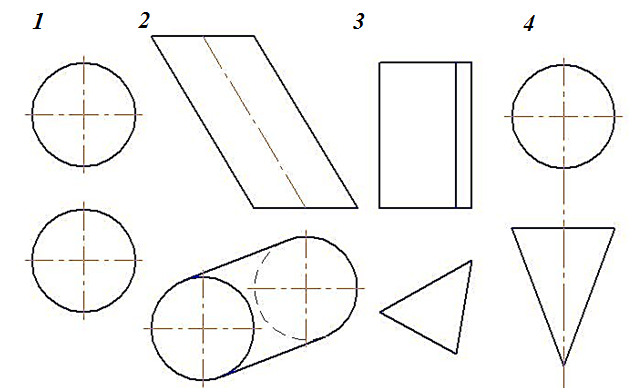
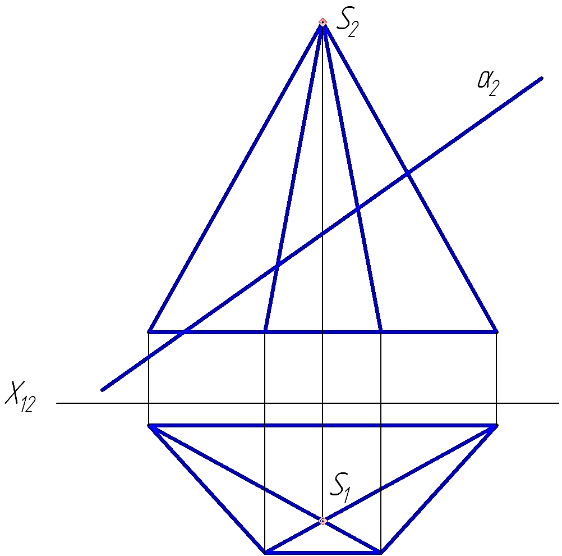
4. На каком чертеже изображен наклонный круговой конус?

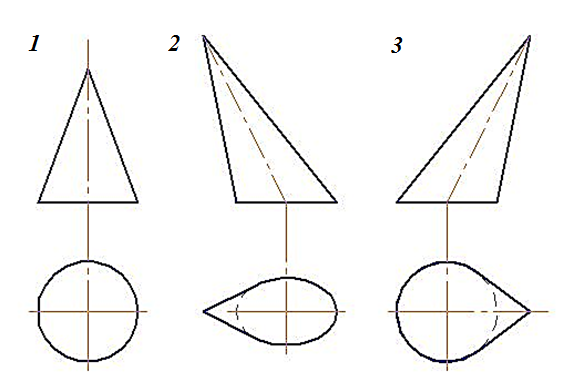
5. На каком чертеже расстояния между ребрами спроецированы в натуральную величину?

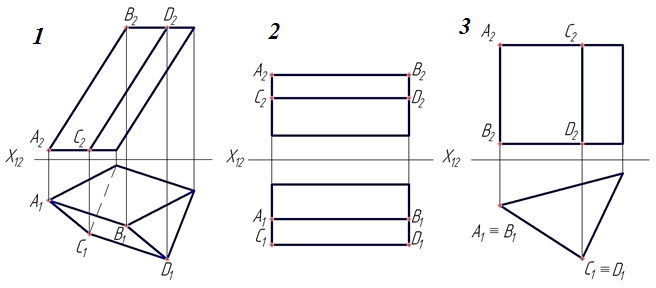
6. На каком чертеже видимость ребер определена ошибочно?

7. выберите правильный ответ – плоскости α, β, γ, δ и ε рассекают конус вращения:

1 α по гиперболе; β по окружности; γ по эллипсу; ε по параболе; δ по треугольнику.

2 α по эллипсу; β поокружности; γ попараболе; δ по треугольнику; ε по гиперболе.

3 α по параболе; β поокружности; γ поэллипсу; δ по треугольнику; ε по гиперболе.

4 α по гиперболе; β поокружности; γ поэллипсу; δ по треугольнику; ε по параболе.

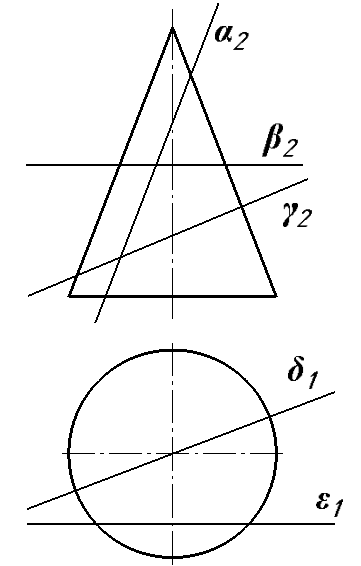
8. Какая фигура получается в сечении данного многогранника плоскостью α?

1 - треугольник 2 - четырехугольник

3 - пятиугольник 4 - шестиугольник

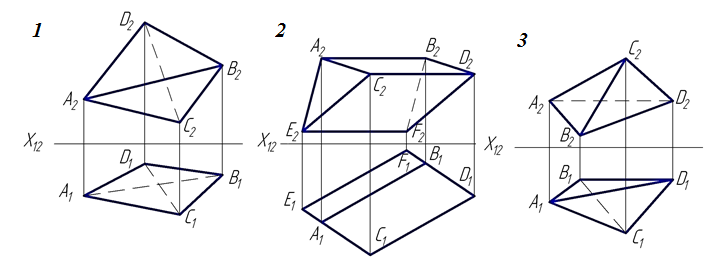
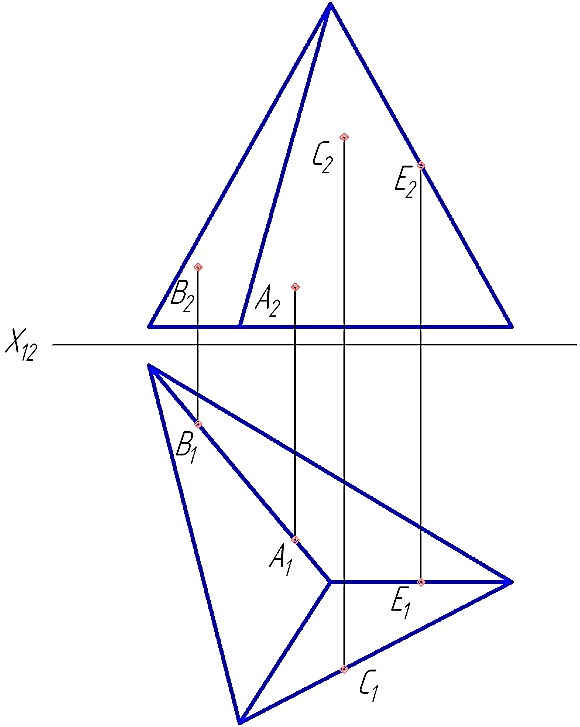
9. Какая из четырех точек лежит на поверхности пирамиды?

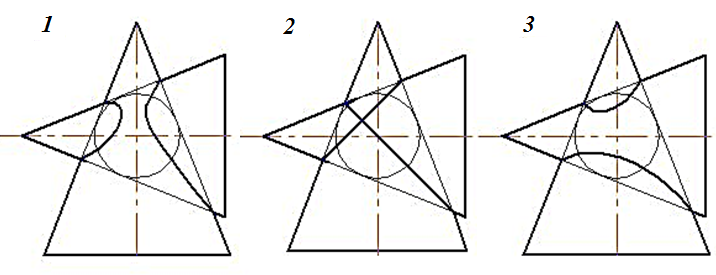
1 – А 2 – В 3 – С 4 – Е

10. Какая из пяти точек лежат на поверхности цилиндра?

1 – А 2 – В 3 – С 4 – D 4 – Е

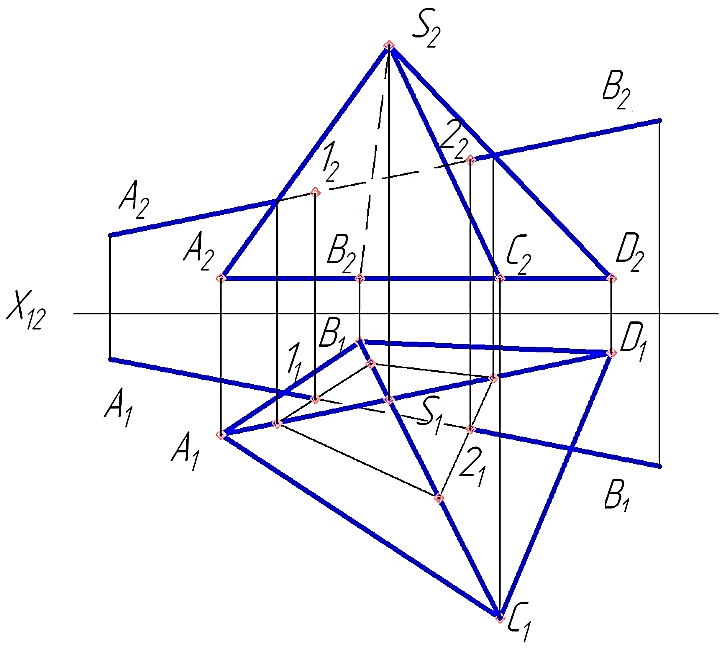
11. И трех вариантов укажите тот, где дан правильный порядок операций нахождения точек пересечения отрезка АВ с поверхностью пирамиды:

1 - а→в→г→б 2 - в→а→г→б 3 - а→г→в→б

а) Построить контур сечения пирамиды вспомогательной плоскостью.

б) Определить видимость отрезка АВ относительно пирамиды.

в) Провести через отрезок АВ вспомогательную проецирующую плоскость.

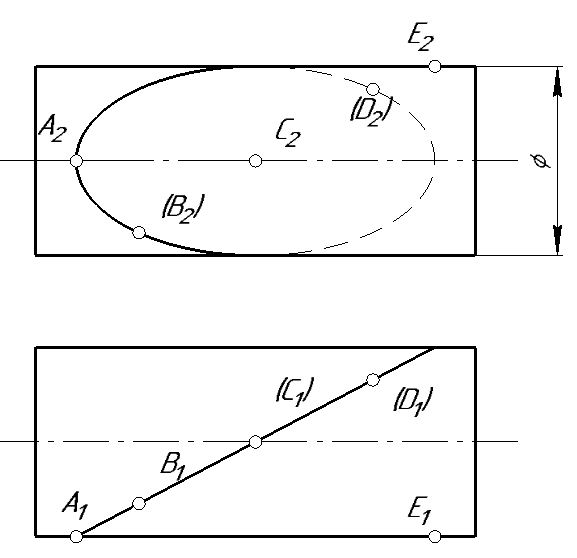
г) Найти точку пересечения отрезка АВ с контуром пересечения.

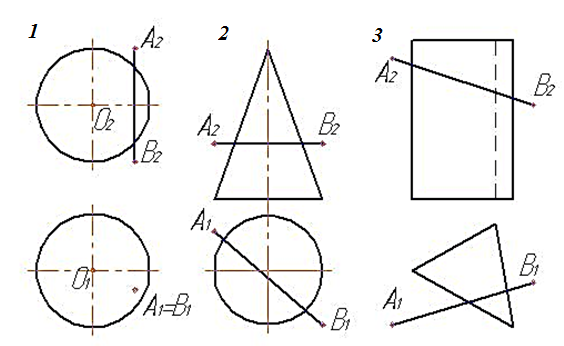
12. На каком чеотеже построение точек пересечения отрезка АВ с поверхностью не требует дополнительных построений?

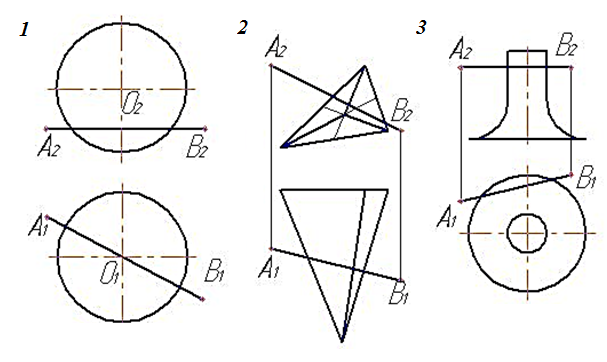
13. На каком чертеже отрезок АВ не пересекает заданную поверхность?

14. На каком чертеже точки пересечения отрезка АВ с поверхностью определены с помощью вспомагательной фронтально-проецирующей плоскости? (След плоскости не обозначен)

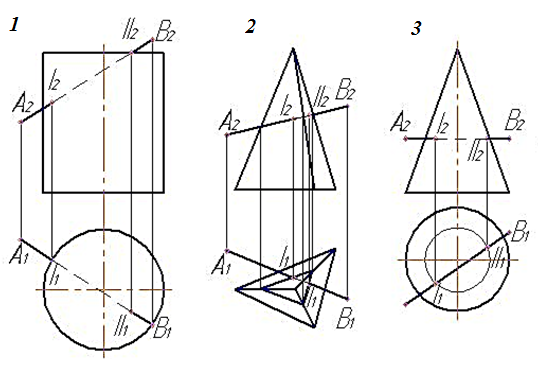
15. На каком чертеже точки пересечения отрезка АВ с поверхностью определены с помощью вспомагательной гооризонтальной плоскости уровня? (След плоскости не обозначен)

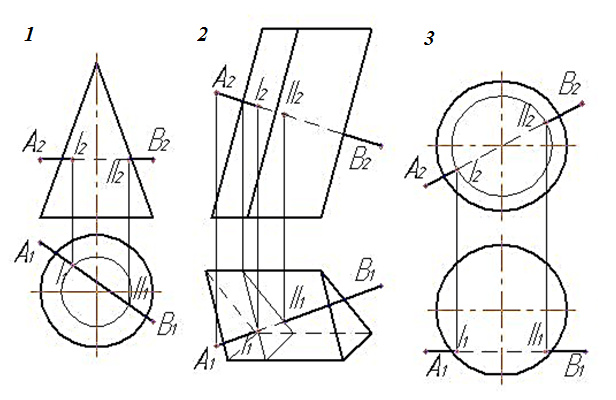
16. На котором чертеже неправильно найдена точка пересечения прямой а с поверхностью многогранника?

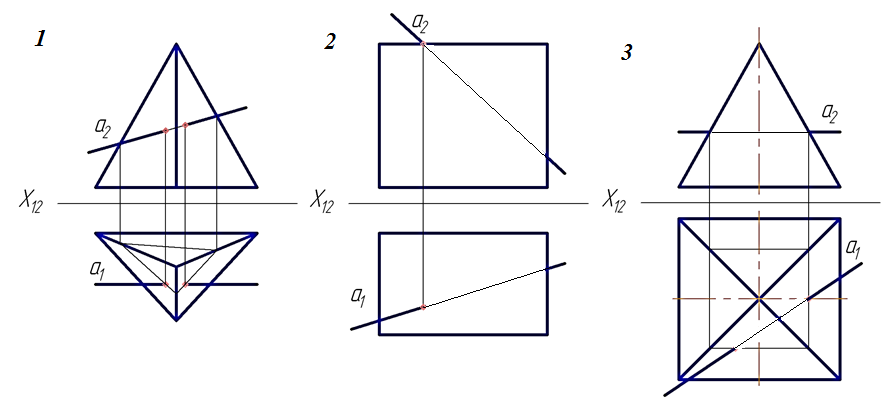
17. На котором чертеже изображены многогранники, пересекающиеся по одной замкнутой линии?

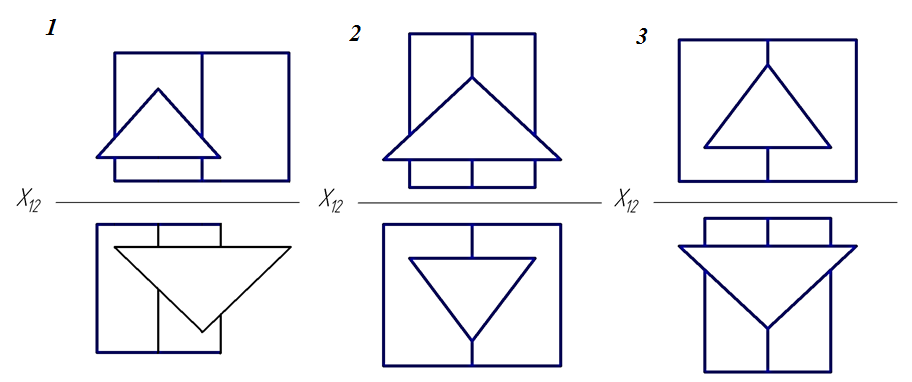
18.Поверхности призмы и конуса пересекаются

по дугам …

1 - окружность→ гиперболы→ эллипсы;

2 - парабола→ гиперболы→ эллипсы;

3 - окружность→ параболы→ эллипсы;

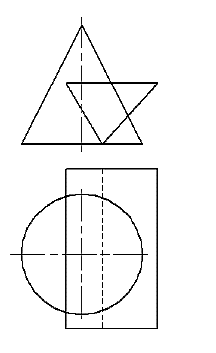
19.Линию пересечения заданных тел можно определить с использованием посредника …

1 – фронтально-проецирующей плоскости

2 – горизонтальной или фронтальной плоскостей уровня

3 – горизонтально-проецирующей плоскости

4 – вспомогательной сферы

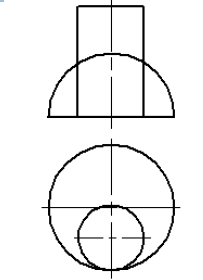
20. На каком чертеже можно построить линию пересечения тел с использованием способа концентрических сфер?

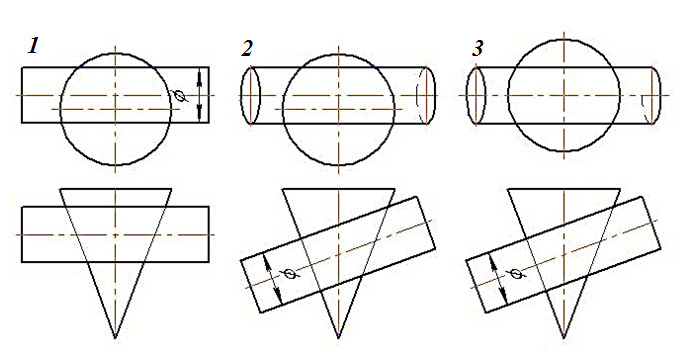
21. На каком чертеже правильно изображена линия пересечения поверхностей (оси поверхностей пересекаются и параллельны плоскости π₂)

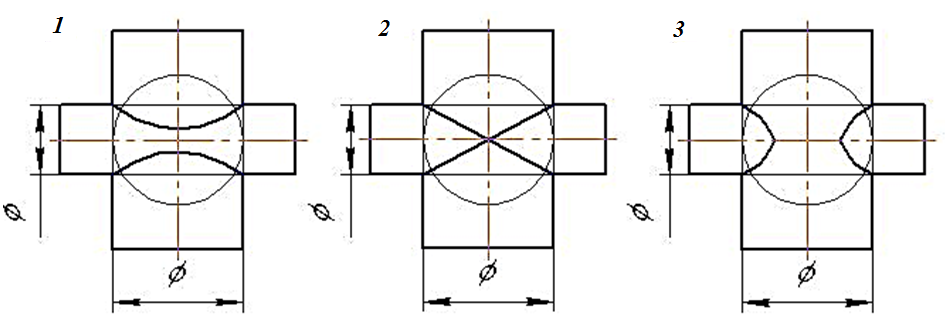
22. На каком чертеже правильно изображена линия пересечения поверхностей (оси поверхностей пересекаются и параллельны плоскости π₂)?

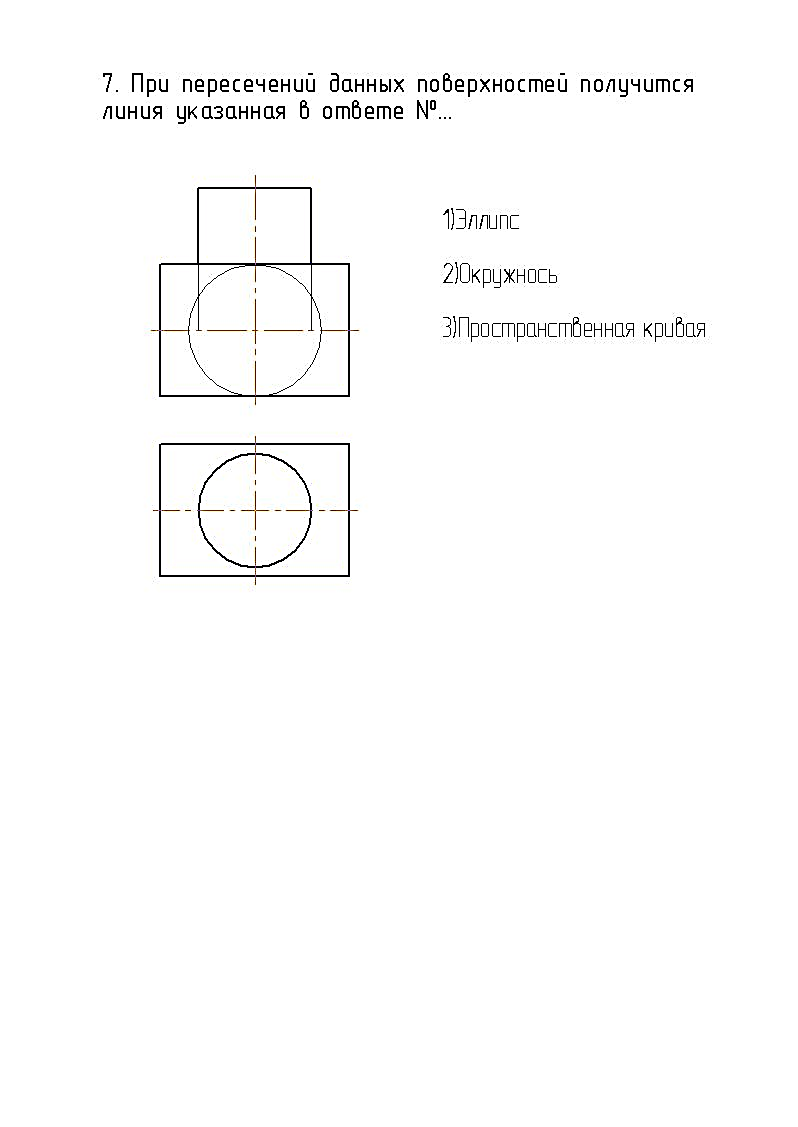
23. При пересечении данных поверхностей получится линия …

1 – эллипс 2 – окружность 3 – кривая четвертого порядка

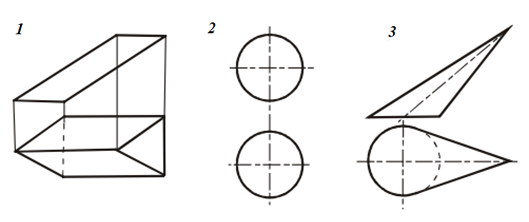
24.Развёртки классифицируются на:

1 – полные 2 – усечённые 3 – точные 4 – приведённые

25.К приближенным разверткам относится …

1 – развертки призм 2 – развертки пирамид

3 – развертки конусов 4 – развертки сфер

26. На каком чертеже изображена условно развертываемая поверхность?

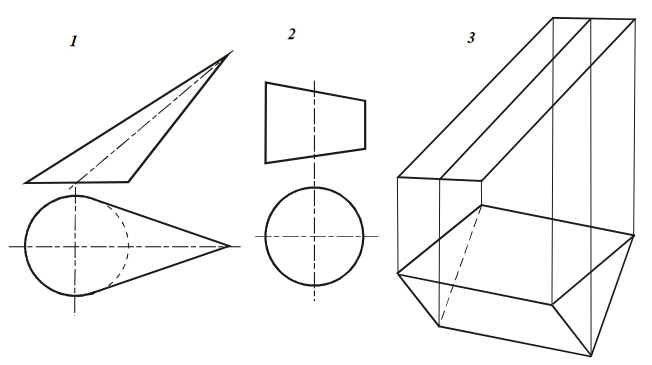
27. Для каких поверхностей при построении развертки целесообразно применить способ нормального сечения?

28.Длина стороны прямоугольника Пd равна

1 – Пd=πd 2 - Пd=2πН 3 – Пd=πR 4 – Пd=πH

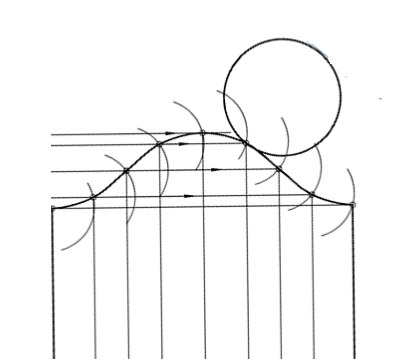
29.На рисунке показана часть развёртки…

1 - прямого кругового конуса 2 - наклонного конуса

3 - наклонного кругового цилиндра 4 - прямого кругового цилиндра

30. Развертка прямой призмы с параллельным основанием изображена на ….

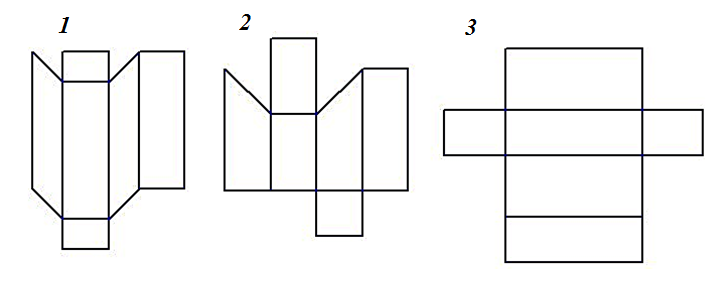
Ответы: 1 – 1; 2– 2; 3 – 3; 4 – 3; 5 – 3; 6 – 1; 7 – 3; 8 – 3; 9 – 4; 10 – 1; 11 – 2; 12– 3; 13 – 3; 14 – 2; 15 – 1; 16 – 3; 17 – 1; 18– 3; 19 – 2; 20 – 3; 21 – 3; 22 – 2; 23 – 3; 24 – 3; 25– 3; 26 – 2; 27 – 3; 28 – 1; 29 – 3; 30 – 3.