Присоединение системы координат к системе плоскостей проекций
Точку в пространстве можно задать или на чертеже (проекциями) или координатами: существуют система плоскостей проекций и система координат. Задание объектов по координатам используется в компьютерной графике.
Рассмотрим вариант присоединения системы координат к системе плоскостей проекций, который будем использовать при решении задач.
Расположим систему координат на оси чертежа x12. (рис. 1.11).
Три основные плоскости проекций (P1^P2^P3) могут рассматриваться и как координатные плоскости. П3 - профильная плоскость проекций.
Начало координат 0 - в точке пересечения плоскостей проекций.
| А Û (А1,А2) êxА ê= ê0 A12ê êyА ê= êA1A12ê êzA ê= êA2A12ê êA1A12ê=êA3A23| A2A3 ^ z |  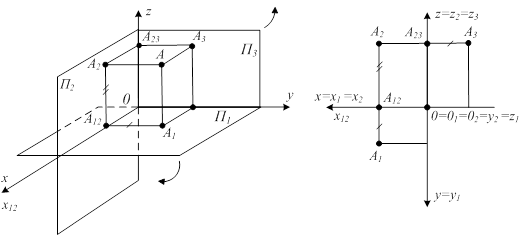 |
Рисунок 1.11
Хотя объект однозначно определяется двумя проекциями, в некоторых случаях используются трехкартинные эпюры (комплексные чертежи). Например, при нахождении точки на профильной прямой - прямой, параллельной профильной плоскости проекций (рис. 1.12).
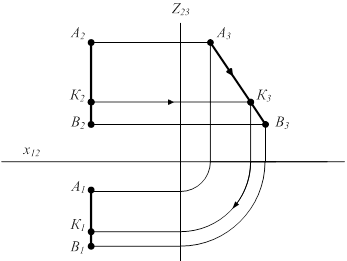
Рисунок 1.12
Вопросы для самоконтроля:
1) Перечислите основные разделы и задачи курса «Инженерной графики».
2) Что называется начертательной геометрией, и какой ее основной метод?
3) Что включает в себя аппарат проецирования?
4) Приведите виды проецирования и их отличия.
5) Перечислите свойства проецирования.
6) Что называется обратимым чертежом?
7) Опишите способ проекций с числовыми отметками.
8) Что называется аксонометрическими проекциями? Дайте определение основной теоремы параллельной аксонометрии.
9) Перечислите стандартные аксонометрические проекции.
10) Дайте определение комплексного чертежа или эпюра Монжа.
11) Постройте чертеж точек, лежащих в 1-4 четвертях.
12) Постройте чертеж точек, лежащих в плоскостях P1 и P2.
13) Отобразите систему координат в системе проекций.
Задание основных элементов на чертеже
Определитель основных геометрических элементов и фигур
Фигура считается заданной в пространстве и на чертеже, если для этой фигуры можно построить сколько угодно точек ей принадлежащих.
Фигура может быть задана однозначно с помощью алгебраического уравнения или проекциями на чертеже.
Совокупность геометрических элементов и правил задающих геометрическую фигуру в пространстве называется ее определителем.
Определитель фигуры состоит из двух частей: F(Г)[А]
где (Г) - набор геометрических элементов, геометрическая часть;
[А] - совокупность алгебраических правил, алгоритмическая часть.
Все вместе геометрические и алгоритмические части задают фигуру на чертеже.
Прямая. Задание прямой линии на чертеже
Если имеем в пространстве две точки, то через них можем провести прямую и притом только одну.
На чертеже прямая может быть задана проекциями двух точек, либо проекциями всей прямой.
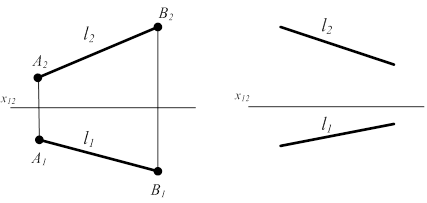
Рисунок 2.1
Задание плоскости на чертеже
Всякая плоскость в пространстве и на чертеже задается своим определителем, который состоит в геометрической части из 3 точек, не лежащих на одной прямой; точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
На комплексном чертеже плоскость задается проекциями ее определителя.
Если плоскость задана на чертеже, то можно построить сколько угодно точек, ей принадлежащих ® алгоритмическая часть определителя поверхностей.
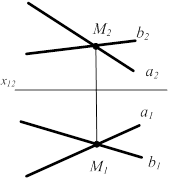
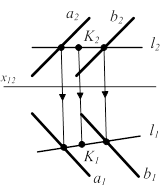
КÎS(АВС) (рис.2.2 а) КÎГ(a||b) (рис.2.2 г)
Геометрические определители плоскости: 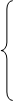 а) S(А,В,С) или D( АВС) а) S(А,В,С) или D( АВС)  б) R (А,b) в) T (а∩b) г) G (а||b) б) R (А,b) в) T (а∩b) г) G (а||b) | 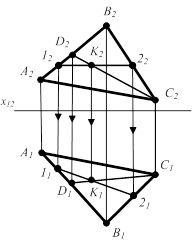 | 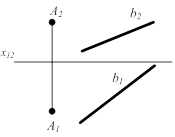 |
| а) | б) | |
 |  | |
| в) | г) |
Рисунок 2.2
