Рабочая тетрадь для аудиторной работы
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.
Рабочая тетрадь для аудиторной работы
студента группы ___________________
_____________________________________________
Составители: Калиничев В.Н., Некоз С.Ю., Назаров А.П.
Москва 2016
ВВЕДЕНИЕ.
Одним из условий успешного освоения курса инженерной графики является систематическое решение задач по основным разделам курса.
Приходя на практические занятия студент должен:
- проработать соответствующий методический материал по теме;
- иметь при себе чертёжные принадлежности: простые карандаши марки 2Т и ТМ, два треугольника, транспортир, циркуль и ластик, а также данный альбом или методические указания и папку для черчения.
Все построения выполняются острозаточенным карандашом. Линии проекционной связи и все линии вспомогательных построений следует проводить сплошными тонкими линиями карандашом Т или 2Т. Полученные результаты (построенный геометрический образ – точка, линия, фигура и т.п.) на всех проекциях выполняются карандашом ТМ. Все линии построений, проведённые при решении задач, необходимо сохранять. Буквенные и числовые обозначения на чертежах должны быть выполнены чертёжным шрифтом размер 3,5 или 5 по ГОСТ 2.304-81.
Решенные задачи по каждому заданию студент должен представить преподавателю в конце занятия. Студенты, не успевшие выполнить задачи очередной работы, заканчивают их дома и представляют преподавателю в часы консультаций, при этом студент должен дать пояснения по решению каждой задачи.
Решение каждой задачи инженерной графики обычно состоит из двух этапов – решение в пространстве и выполнение её на чертеже. При этом полезно прибегать к моделированию изучаемых геометрических форм простейшими средствами (карандаш, линейка, тетрадь и т.д.). Приступая к решению задачи, следует составить сначала ясный план решения в пространстве, а затем уже осуществить его выполнение на чертеже. Для решения некоторых наиболее трудных задач вместе с условием даётся алгоритм, который необходимо записать с помощью условных обозначений на чертеже данной задачи.
Для успешного решения задач от студента требуются знания основных теорем элементарной геометрии – планиметрии и стереометрии.
При графических решениях задачи точность ответа зависит не только от выбора правильного пути её решения, но и от точности геометрических построений. Поэтому, решая задачу, необходимо пользоваться качественным инструментом и аккуратно выполнять все геометрические построения.
К итоговой аттестации по инженерной графике допускаются студенты, выполнившие все работы.
На титульном листе и в верхней части каждой страницы студент должен разборчиво написать свои фамилию и инициалы, а также шифр группы.
Важно! Если в условии задачи не указан масштаб, то единица масштаба принимается равной 1 см.
1. Метод проекций, комплексный чертёж точки.
1. Значением каких координат определяются горизонтальная, фронтальная и профильная проекции точки? (ответы дать в таблице).
| Проекция точки | Высота | Широта | Глубина |
| Горизонтальная | |||
| Фронтальная | |||
| Профильная |
2. Где находятся горизонтальная проекция точки, принадлежащей фронтальной плоскости П2 и фронтальная проекция точки, принадлежащей горизонтальной плоскости П1?
3. В каком октанте все координаты точки имеют отрицательные значения?
4. Как расположена точка C относительно плоскостей проекций П1 и П2, если её горизонтальная и фронтальная проекции совпадают и располагаются под осью проекций?
5. По наглядному изображению точек A, B, C и D построить их комплексный чертеж.
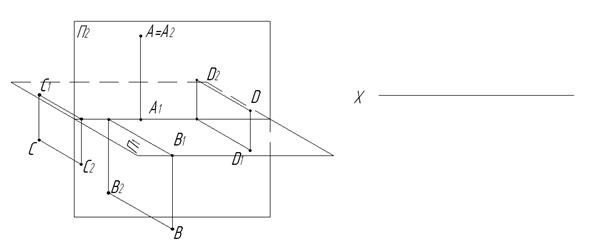
6. Построить комплексный чертёж точки A, отстоящей от плоскости П1 на расстоянии 3.5 ед. масштаба, а от плоскости П2 на 2 ед. масштаба и точки B, если она лежит в плоскости П1 и отстоит от плоскости П2 на 2 ед. масштаба. Построить горизонтальные и фронтальные проекции точки C, у которой глубина в два раз больше её высоты и точки D, высота которой равна 3 ед. масштаба, а глубина равна 0. Точки A и Bнаходятся в первой четверти.
7. Определить положение точек C, D и Е относительно плоскости проекций (указать высоту и глубину этих точек в мм).
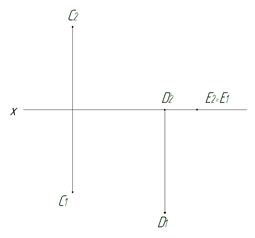
8. Построить комплексный чертёж точек A, В, С и D, находящихся в разных четвертях и отстоящих от плоскости П1 на 10 мм, а от плоскости П2 на 20 мм.
9. Построить комплексный чертёж точки B симметричной точке A (10,10, 30) относительно:
а) пл. П1; б) пл. П2; в) оси проекций Х
Построения а), б) и в) выполняются на трех отдельных трехкартинных чертежах.
2. Трёхкартинный чертёж, прямая линия, моделирование
Алгоритм.
- выбрать на прямой m произвольную точку B и построить на горизонтальной проекции отрезка АВ (отрезок А1В1), как на катете, прямоугольный треугольник с углом 60° при вершине А;.
- катет прямоугольного треугольника – В1В*, лежащий против угла 60°, равен разности высот точек A и B;
- проведя линию проекционной связи через точку B, отложить по ней на фронтальной проекции полученную разность высот точек A и В.
4. Взаимное расположение двух прямых линий.
Алгоритм.
- 
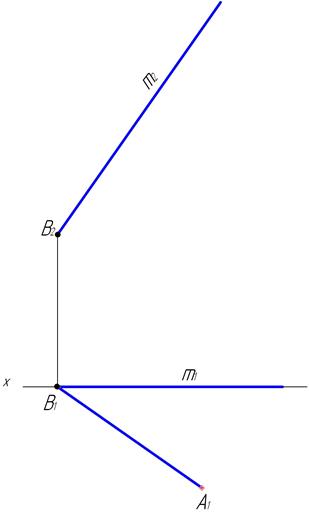определить положение прямой m в пространстве и на основании теоремы о проекции прямого угла провести фронтальную проекцию линии, на которой лежит сторона ВА и найти на ней фронтальную проекцию точки А.
- определить истинную длину стороны квадрата – отрезка ВА.
- построить вторую сторону квадрата – ВС на стороне m.
- достроить стороны CD и DA, параллельные сторонам АВ и ВС.
5. Плоскость. Прямая и точка в плоскости.
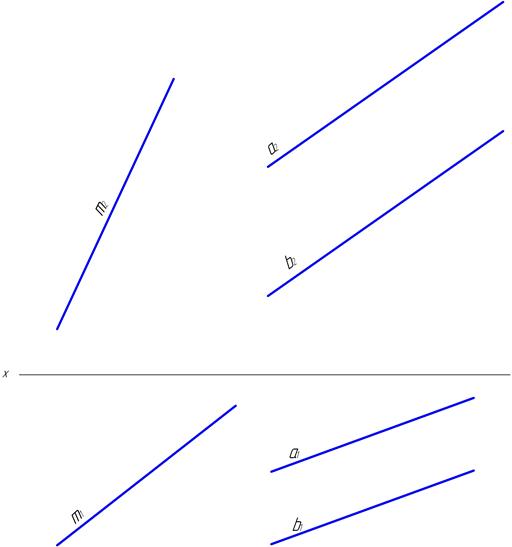
29. Как расположены по отношению к плоскостям проекций плоскости, заданные на чертеже прямыми а и b (указать в таблице какие это плоскости: общего положения, проецирующие, уровня)?
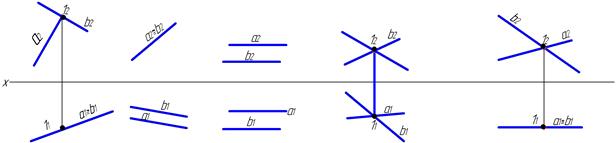
а б в г д
| а | б | в | г | д | |
| Название плоскости |
30. Указать в таблице какое положение относительно плоскостей проекций занимают плоскости заданные на чертеже?
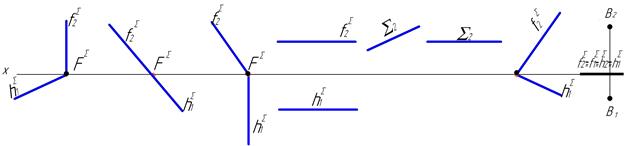
а б в г д е ж з
| а | б | в | г | д | е | ж | з | |
| Название плоскости |
31. Даны точка А и плоскость. Определить и указать в таблице принадлежит ли точка А плоскости?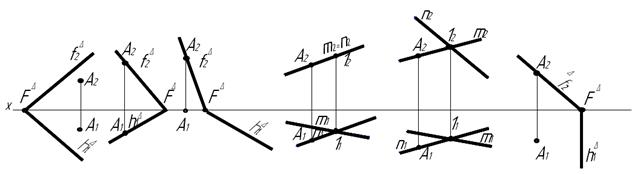 
а б в г д е
| а | б | в | г | д | е | |
| Расположение точки А относительно плоскости |
32. На каком из чертежей прямая m принадлежит плоскости?
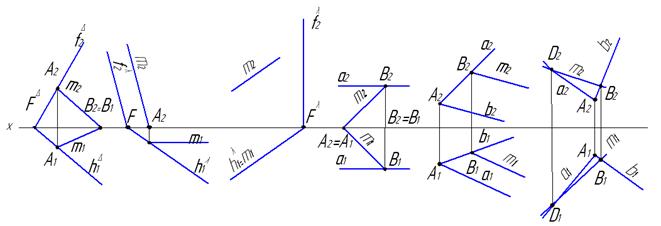
а б в г д е
| а | б | в | г | д | е | |
| Принадлежность прямой m плоскости |
33. Построить недостающие проекции точек принадлежащих плоскости S?
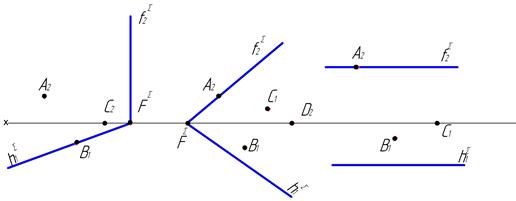
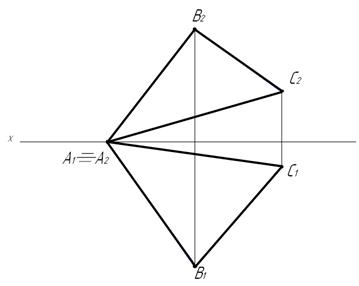
34. Построить в плоскости D (mxn) треугольник АВС и произвольную точку D, удалённую от плоскости П2 на 25 мм.
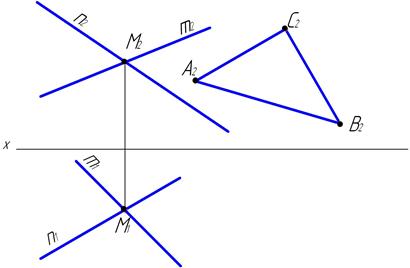
35. Через прямую m провести горизонтально-проецирующую и профильно-проецирующую плоскости.
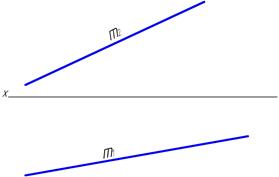
36. Построить фронтальную проекцию прямой l и горизонтальную проекцию прямой d, лежащих в плоскости S.
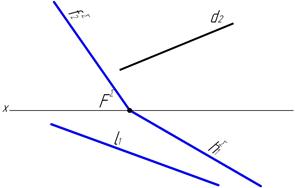
37. Построить следы плоскостей D (А, В, С) и L (fxh).
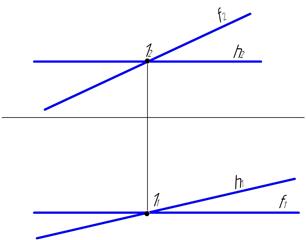
6. Главные линии плоскости. Определение углов наклона плоскости к плоскостям проекций. Элементы залегания структурной плоскости.
38. В плоскости Y (А, В, С) провести горизонтальную прямую, отстоящую от плоскости П1 на 3.2 ед. масштаба, а через точку В провести фронтальную прямую.
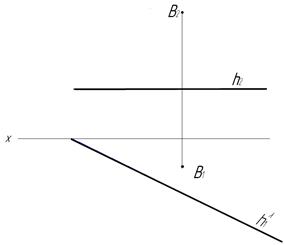
39. Построить горизонтальную проекцию горизонтали h плоскости L (hl; В).
40. Определить угол наклона плоскости D (h Dx f D) к плоскостям П1, P2 и P3.
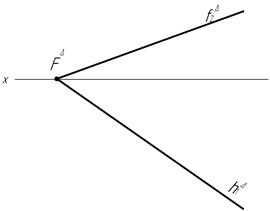
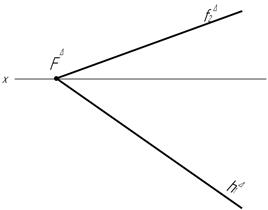
41. Буровые скважины, заложенные в точке А (вертикальная) и в точках В и С (наклонные), вскрыли в точках D,E и F слой горной породы. Определить элементы залегания (азимут падения, азимут простирания и угол падения) слоя и наклонную глубину скважин В и С.
| Координаты точек в мм | A | B | C |
| Азимут падения скважины | вертикальная | 40° | 206° |
| Фронтальная проекция зенитного угла | - | 22° | 16° |
| Глубины точек в метрах | D | E | F |
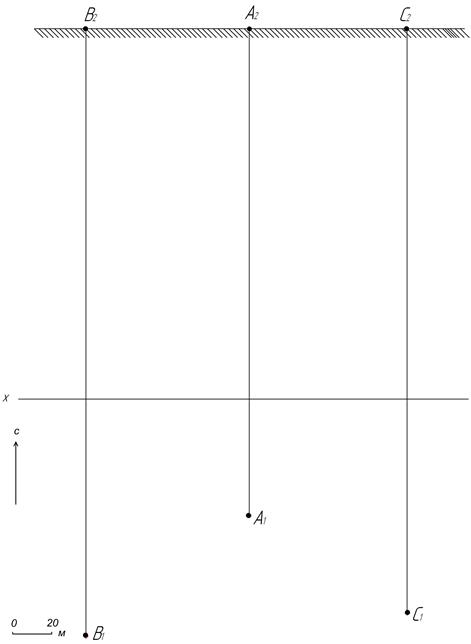
7. Взаимное расположение двух плоскостей.
42. На каком из чертежей изображены параллельные плоскости?
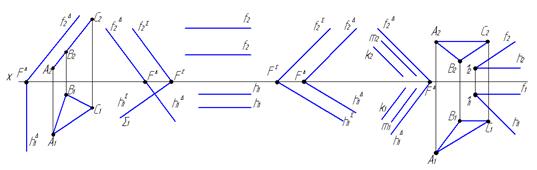
а б в г д е
43. Построить линии пересечения двух плоскостей S x L и D x Y.
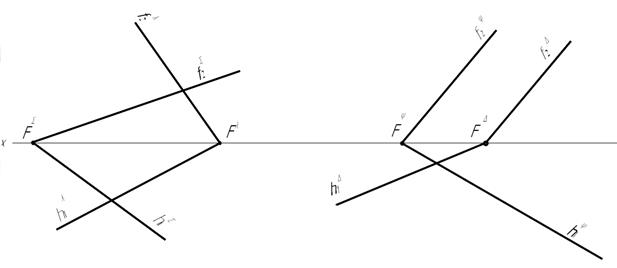
44. Через точку К провести плоскость D, параллельную плоскости L(m // n).
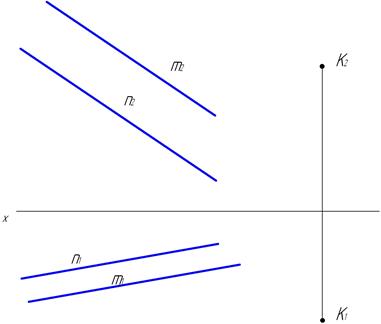
45. Построить плоскость S // L(axb) и отстоящую от неё на 3.0 ед. масштаба вниз.
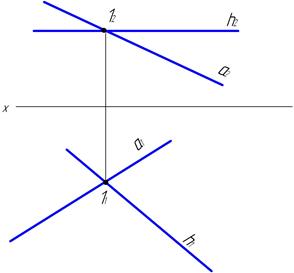
46. Построить линию пересечения двух плоскостей Y(А, В, С) и Q(D, Е, F) .
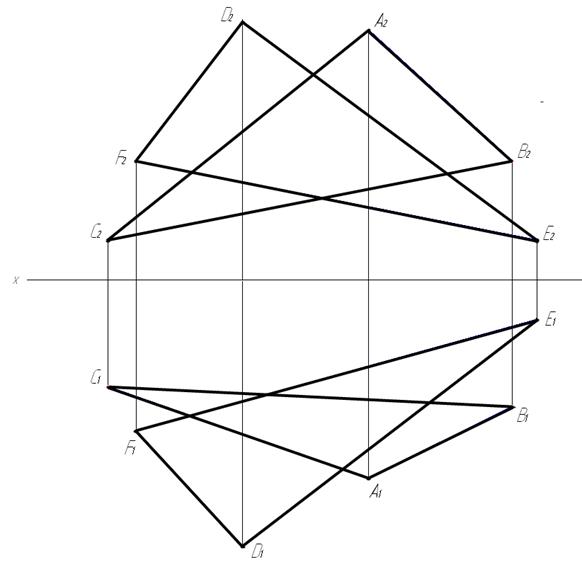
8. Взаимное расположение прямой и плоскости.
Указания к решению задачи.
Угол между прямой и плоскостью определяется углом m, образованным прямой и её ортогональной проекцией на эту плоскость. Построение проекции угла m требует определения двух точек, первая из которых является точкой пересечения данной прямой m с плоскостью S, а вторая – основанием перпендикуляра, опущенного из произвольной точки на ту же плоскость. В целях сокращения построений необходимо определить угол b, дополняющий до 90° искомый угол m.
Алгоритм.
- из произвольной точки М, принадлежащей прямой m, проводится перпендикуляр n к плоскости D(a//b).
- вращением вокруг прямой уровня определяют угол между прямыми m и n – угол b.
- Вычисляется угол m=90°- b.
11. Многогранники. Пересечение многогранника плоскостью.
Приложение
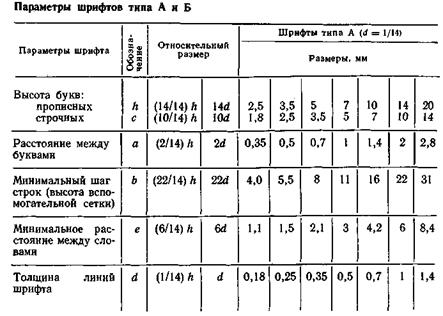
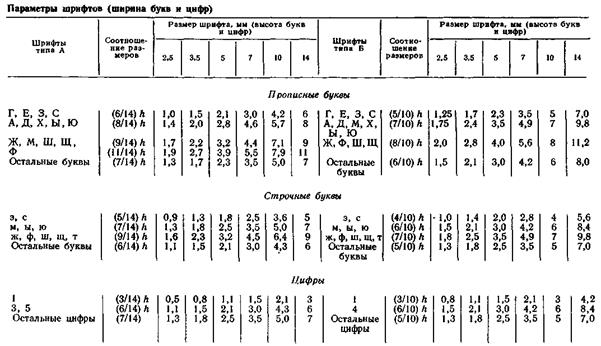
Шрифт (ГОСТ 2.304-81)
Таблица 1
продолжение таблицы 1
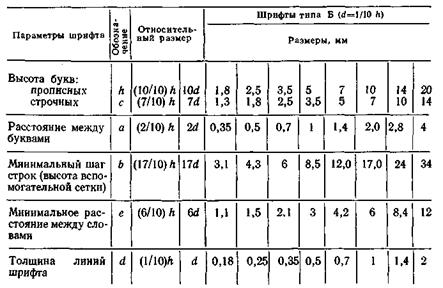
Таблица 2
Список литературы
1. Ломоносов Г.Г. Инженерная графика. М., Недра, 1984
2. Гордон В.О. Курс начертательной геометрии. 2009г.
3. Чекмарев А.А. Инженерная графика. 2010 г.
4. Локтев О.В. Краткий курс начертательной геометрии.
Оглавление.
1. Метод проекций, комплексный чертёж точки.......................................................................... 3
2. Трёхкартинный чертёж, прямая линия, моделирование
буровой скважины прямой линией............................................................................................ 5
3. Прямая и точка. определение истинной длины отрезка прямой общего положения и углов её наклона к плоскостям проекций................................................................................................. 7
4. Взаимное расположение двух прямых линий. Взаимно перпендикулярные прямые...... 9
5. Плоскость. Прямая и точка в плоскости................................................................................ 12
6. Главные линии плоскости. определение углов наклона плоскости к плоскостям проекций. элементы залегания структурной плоскости......................................................................... 15
7. Взаимное расположение двух плоскостей............................................................................... 17
8. Взаимное расположение прямой и плоскости. Взаимно перпендикулярные плоскости. 19
9. Метод перемены плоскостей проекций.................................................................................... 21
10. Метод вращения.......................................................................................................................... 23
11. Многогранники. пересечение многогранника плоскостью. Определение истинного вида фигуры сечения.................................................................................................................................................. 26
12. Пересечение кривой поверхности с плоскостью.................................................................... 28
13. Пересечение поверхности с прямой линией. Плоскости касательные к поверхностям. 31
14. Пересечение поверхностей......................................................................................................... 34
Приложение...........................................................................................................................................35
Список литературы............................................................................................................................ 37
Оглавление........................................................................................................................................... 37
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.
Рабочая тетрадь для аудиторной работы
студента группы ___________________
_____________________________________________
Составители: Калиничев В.Н., Некоз С.Ю., Назаров А.П.
Москва 2016
ВВЕДЕНИЕ.
Одним из условий успешного освоения курса инженерной графики является систематическое решение задач по основным разделам курса.
Приходя на практические занятия студент должен:
- проработать соответствующий методический материал по теме;
- иметь при себе чертёжные принадлежности: простые карандаши марки 2Т и ТМ, два треугольника, транспортир, циркуль и ластик, а также данный альбом или методические указания и папку для черчения.
Все построения выполняются острозаточенным карандашом. Линии проекционной связи и все линии вспомогательных построений следует проводить сплошными тонкими линиями карандашом Т или 2Т. Полученные результаты (построенный геометрический образ – точка, линия, фигура и т.п.) на всех проекциях выполняются карандашом ТМ. Все линии построений, проведённые при решении задач, необходимо сохранять. Буквенные и числовые обозначения на чертежах должны быть выполнены чертёжным шрифтом размер 3,5 или 5 по ГОСТ 2.304-81.
Решенные задачи по каждому заданию студент должен представить преподавателю в конце занятия. Студенты, не успевшие выполнить задачи очередной работы, заканчивают их дома и представляют преподавателю в часы консультаций, при этом студент должен дать пояснения по решению каждой задачи.
Решение каждой задачи инженерной графики обычно состоит из двух этапов – решение в пространстве и выполнение её на чертеже. При этом полезно прибегать к моделированию изучаемых геометрических форм простейшими средствами (карандаш, линейка, тетрадь и т.д.). Приступая к решению задачи, следует составить сначала ясный план решения в пространстве, а затем уже осуществить его выполнение на чертеже. Для решения некоторых наиболее трудных задач вместе с условием даётся алгоритм, который необходимо записать с помощью условных обозначений на чертеже данной задачи.
Для успешного решения задач от студента требуются знания основных теорем элементарной геометрии – планиметрии и стереометрии.
При графических решениях задачи точность ответа зависит не только от выбора правильного пути её решения, но и от точности геометрических построений. Поэтому, решая задачу, необходимо пользоваться качественным инструментом и аккуратно выполнять все геометрические построения.
К итоговой аттестации по инженерной графике допускаются студенты, выполнившие все работы.
На титульном листе и в верхней части каждой страницы студент должен разборчиво написать свои фамилию и инициалы, а также шифр группы.
Важно! Если в условии задачи не указан масштаб, то единица масштаба принимается равной 1 см.
1. Метод проекций, комплексный чертёж точки.
1. Значением каких координат определяются горизонтальная, фронтальная и профильная проекции точки? (ответы дать в таблице).
| Проекция точки | Высота | Широта | Глубина |
| Горизонтальная | |||
| Фронтальная | |||
| Профильная |
2. Где находятся горизонтальная проекция точки, принадлежащей фронтальной плоскости П2 и фронтальная проекция точки, принадлежащей горизонтальной плоскости П1?
3. В каком октанте все координаты точки имеют отрицательные значения?
4. Как расположена точка C относительно плоскостей проекций П1 и П2, если её горизонтальная и фронтальная проекции совпадают и располагаются под осью проекций?
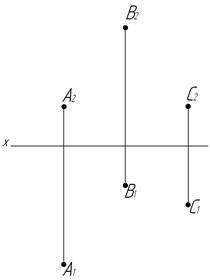
5. По наглядному изображению точек A, B, C и D построить их комплексный чертеж.
6. Построить комплексный чертёж точки A, отстоящей от плоскости П1 на расстоянии 3.5 ед. масштаба, а от плоскости П2 на 2 ед. масштаба и точки B, если она лежит в плоскости П1 и отстоит от плоскости П2 на 2 ед. масштаба. Построить горизонтальные и фронтальные проекции точки C, у которой глубина в два раз больше её высоты и точки D, высота которой равна 3 ед. масштаба, а глубина равна 0. Точки A и Bнаходятся в первой четверти.
7. Определить положение точек C, D и Е относительно плоскости проекций (указать высоту и глубину этих точек в мм).
8. Построить комплексный чертёж точек A, В, С и D, находящихся в разных четвертях и отстоящих от плоскости П1 на 10 мм, а от плоскости П2 на 20 мм.
9. Построить комплексный чертёж точки B симметричной точке A (10,10, 30) относительно:
а) пл. П1; б) пл. П2; в) оси проекций Х
Построения а), б) и в) выполняются на трех отдельных трехкартинных чертежах.
2. Трёхкартинный чертёж, прямая линия, моделирование