Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них

Для треугольника всегда возможны и вписанная окружность и описанная окружность.

Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы. Из всех параллелограммов только в ромб и квадрат можно вписать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг трапеции возможно описать окружность или в трапецию можно вписать окружность если трапеция равнобокая.

Центр описанной окружности

Теорема. Центр описанной около треугольника окружности является точкой пересечениясерединных перпендикуляров к сторонам треугольника.

Центр описанной около многоугольника окружности является точкой пересечения серединных перпендикуляров к сторонам этого многоугольника.

Центр Вписанная окружность

Определение. Вписанная в выпуклый многоугольник окружность — это окружность, которая касается всех сторон этого многоугольника (то есть каждая из сторон многоугольника является для окружностикасательной).

Центр вписанной окружности лежит внутри многоугольника.

Многоугольник, в который вписана окружность, называется описанным.

В выпуклый многоугольник можно вписать окружность, если биссектрисы всех его внутренних углов пересекаются в одной точке.

Центр вписанной в многоугольник окружности — точка пересечения его биссектрис.

Центр вписанной окружности равноудален от сторон многоугольника. Расстояние от центра до любой стороны равно радиусу вписанной окружности По свойству касательных, проведённых из одной точки, любая вершина описанного многоугольника равноудалена от точек касания, лежащих на сторонах, выходящих из этой вершины.

В любой треугольник можно вписать окружность. Центр вписанной в треугольник окружности называется инцентром.

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. В частности, в трапецию можно вписать окружность, если сумма её оснований равна сумме боковых сторон.

В любой правильный многоугольник можно вписать окружность. Около любого правильного многоугольника можно также описать окружность. Центр вписанной и описанной окружностей лежат в центре правильного многоугольника.

Для любого описанного многоугольника радиус вписанной окружности может быть найден по формуле

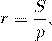где S — площадь многоугольника, p — его полупериметр.

Правильный n-угольник - формулы

Формулы длины стороны правильного n-угольника

1. Формула стороны правильного n-угольника через радиус вписанной окружности:

a = 2r · tg	180°
n

a = 2r · tg	π
n

2. Формула стороны правильного n-угольника через радиус описанной окружности:

a = 2 R · sin	180°
n

a = 2 R · sin	π
n

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны:

r = a : (2tg	180°	)
n

r = a : (2tg	π	)
n

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны:

R = a : (2sin	180°	)
n

R = a : (2sin	π	)
n

Правильный треугольник

Формулы правильного треугольника:

1. Формула стороны правильного треугольника через радиус вписанной окружности: a = 2r √3

2. Формула стороны правильного треугольника через радиус описанной окружности: a = R√3

3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:

r =	a√3

4. Формула радиуса описанной окружности правильного треугольника через длину стороны:

R =	a√3

5. Формула площади правильного треугольника через длину стороны:

S =	a2√3

6. Формула площади правильного треугольника через радиус вписанной окружности: S = r² 3√3

7. Формула площади правильного треугольника через радиус описанной окружности:

S =	R2 3√3

8. Угол между сторонами правильного треугольника: α = 60°

Правильный четырехугольнику - квадрат.

Формулы правильного четырехугольника:

1. Формула стороны правильного четырехугольника через радиус вписанной окружности: a = 2r

2. Формула стороны правильного четырехугольника через радиус описанной окружности: a = R√2

3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:

r =	a

4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:

R =	a√2

5. Формула площади правильного четырехугольника через длину стороны: S = a²

6. Формула площади правильного четырехугольника через радиус вписанной окружности: S = 4 r²

7. Формула площади правильного четырехугольника через радиус описанной окружности: S = 2 R²

8. Угол между сторонами правильного четырехугольника: α = 90°

Формулы правильного шестиугольника:

1. Формула стороны правильного шестиугольника через радиус вписанной окружности:

a =	2√3	r

2. Формула стороны правильного шестиугольника через радиус описанной окружности: a = R

3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:

r =	a√3

4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны: R = a

5. Формула площади правильного шестиугольника через длину стороны:

S =	a2 3√3

6. Формула площади правильного шестиугольника через радиус вписанной окружности: S = r² 2√3

7. Формула площади правильного шестиугольника через радиус описанной окружности:

S =	R2 3√3

8. Угол между сторонами правильного шестиугольника: α = 120°

Значение числа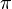 (произносится «пи») — математическая константа, равная отношению

длины окружности к длине её диаметра, оно выражается бесконечной десятичной дробью.

Обозначается буквой греческого алфавита «пи». Чему равно число пи? В простых случаях хватает знать первые 3 знака (3,14).

53. Найдем длину дуги окружности радиуса R, отвечающей центральному углу в n°

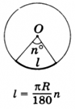
Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.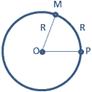

Градусная мера угла в 1 радиан равна:

Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.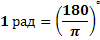

И наоборот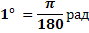

Так как π = 3,14, то 1 рад = 57,3°

Если угол содержит a радиан, то его градусная мера равна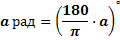

И наоборот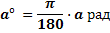

Обычно при обозначении меры угла в радианах наименование «рад» опускают.

Например, 360° = 2π рад, пишут 360° = 2π

В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.