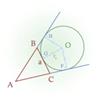
Свойства вписанной в треугольник окружности

1. Центр вписанной в треугольник окружности (на рис. 1 – точка О) лежит на пересечении биссектрис треугольника (на рис.1 – АО, ВО и СО).
2. В любой треугольник вписывается окружность и притом только одна.
3. Радиус вписанной в треугольник окружности равен:

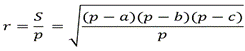
Где S – это площадь треугольника, p - полупериметр треугольника, a, b, c - стороны треугольника.

Вневпи́санная окружность треугольника — окружность, касающаяся одной из сторон треугольника и продолжений двух других его сторон. У любого треугольника существует три вневписанных окружности (в отличие от единственной вписанной).

Существование и единственность вневписанной окружности обусловлены тем, что биссектрисы двух внешних углов треугольника и биссектриса внутреннего угла, не смежного с этими двумя, пересекаются в одной точке, которая и является центром такой окружности.

Вневписанная окружность

Ну вот, пора приступать к самому непонятному. Что же это за зверь такой: «вневписанная окружность»? Сначала посмотри на картинку:

Видишь, окружность тоже чего-то касается, но «сидит» как-то снаружи, вне треугольника? Вот поэтому и называется вневписанной.

Окружность называется вневписанной для треугольника, если она касается ОДНОЙ стороны треугольника и продолжений двух других сторон.

Свойства вневписанной окружности

Центр вневписанной окружности в треугольник есть точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру данного треугольника Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны. Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности

Вневписанная окружность треугольника — окружность, касающаяся одной из сторон треугольника и продолжений двух других его сторон. У любого треугольника существует три вневписанных окружности (в отличие от единственной вписанной). ra=S/p−a

Касание окружностей

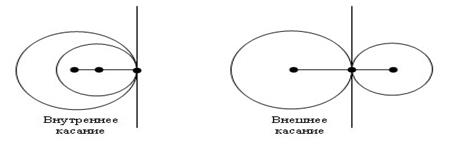
Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Через точку касания можно провести касательную к одной из окружностей, которая является одновременно и касательной к другой окружности. Касание окружностей бывает внутренним и внешним.
Касание называется внутренним, если центры окружностей лежат по одну сторону от касательной.
Касание называется внешним, если центры окружностей лежат по разные стороны от касательной