Основные сведения о конформной проекции Гаусса - Крюгера эллипсоида на плоскости

Конечная практическая цель триангуляционных, полигонометрических работ - определение положения геодезических пунктов на поверхности принятого референц-эллипсоида. Положение этих пунктов может быть определено в различных системах координат. Необходимо вычислять координаты пунктов в такой системе, которая была бы проста и обеспечивала бы наиболее удобное и лёгкое использование координат в разнообразных практических целях.

Такой системой является система плоских прямоугольных координат. В этой системе вычисляют координаты пунктов съёмочного обоснования, для которых координаты пунктов триангуляции являются исходными, производят различного рода расчёты при проектировании, перенесение проектов в натуру и строительстве разнообразных инженерных сооружений. Использование топографических планов существенно облегчается, если на них нанесена сетка координатных линий в прямоугольной системе координат на плоскости. Прямоугольные координаты геодезических пунктов необходимы при использовании геодезических данных для оборонных целей.

Известно, что поверхность эллипсоида не может быть развёрнута на плоскость без искажений, поэтому и не может быть предложена система плоских прямоугольных координат, в которой без искажений было бы выражено взаимное положение точек земной поверхности. Поставленная задача сводится к изображению поверхности эллипсоида на плоскости по некоторому определённому закону. Математический закон (проекция) в общем виде может быть выражен уравнениями

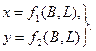(138)

В этих уравнениях x и y - плоские прямоугольные координаты изображаемой на плоскости точки, выраженные как функции геодезических координат той же точки на поверхности эллипсоида.

Требования к выбору проекции:

1) минимальные искажения изображаемых на плоскости элементов поверхности эллипсоида;

2) лёгкость и простота учёта искажений.

- 64 -

Указанным требованиям из числа существующих проекций наилучшим образом удовлетворяет конформная (равноугольная) поперечно - цилиндрическая проекция Гаусса-Крюгера. Эту проекцию предложил К.Ф. Гаусс в 1825-1830 гг. В 1912 г. его соотечественник Л. Крюгер разработал детали применения и дал рабочие формулы для вычисления в этой проекции.

При использовании проекции Гаусса-Крюгера поверхность земного эллипсоида делится меридианами на зоны - сфероидические двуугольники, имеющие постоянную разность долгот. Средний меридиан зоны называют о с е в ы м и его геодезическая долгота обозначается через L_0.

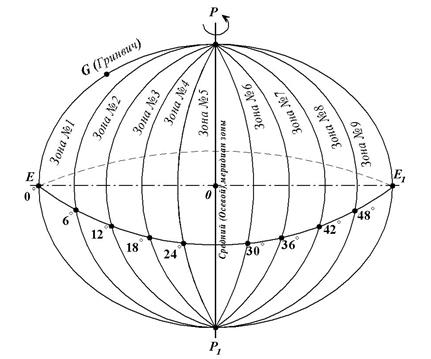
Рис. 33. Зоны в проекции Гаусса- Крюгера

В России и странах СНГ протяжённость зон по долготе установлена в 6°, а в районах, где топографические съёмки выполняют в крупных масштабах, зоны по долготе имеют протяжённость 3°.

- 65 -

Осевые меридианы шестиградусных зон совпадают с центральными меридианами листов карты масштаба 1:1000 000. Порядковый номер зоны определяется по формуле

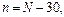(139)

где N - номер колонны листа карты масштаба 1:1000 000.

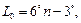Долготы осевых меридианов шестиградусных зон вычисляют по формуле

(140)

где n - номер зоны.

Прямоугольные координаты x , y в пределах зоны определяются относительно экватора и осевого меридиана, которые изображаются прямыми линиями (рис. 34).

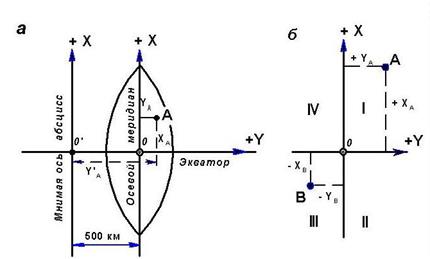Рис. 34. Прямоугольные координаты в проекции Гаусса- Крюгера

В пределах территории СНГ абсциссы координат Гаусса-Крюгера положительные; ординаты положительные к востоку, отрицательные - к западу от осевого меридиана. Чтобы избежать отрицательных значений ординат, точкам осевого меридиана условно приписывают значение

y = 500 000 м с обязательным указанием номера зоны перед численным значением ординаты точки. Например, если точка находится в зоне с номером 8 в 37625 м к востоку от осевого меридиана, то значение ординаты запишется так: y= 8 537 625 м; если точка расположена к западу от осевого меридиана этой же зоны, например, на 126 377 м, то ордината

- 66 -

данной точки запишется в виде y = 8 373 623 м.

В конформной проекции углы треугольников триангуляции не искажаются, т. е. остаются такими же, как на поверхности земного эллипсоида. Масштаб изображения линейных элементов на плоскости постоянен в данной точке и не зависит от направления (азимута) этих элементов; линейные искажения на осевом меридиане равны нулю и постепенно возрастают по мере удаления от него; на краю шестиградусной зоны они достигают наибольшей величины, равной 1:1000, а на краю трёхградусной зоны - 1:5000.

Все линии на поверхности земного эллипсоида, за исключением осевого меридиана и экватора, изображаются на плоскости кривыми. Так, например, стороны треугольника с вершинами 1, 2, 3, построенного на эллипсоиде (рис. 35, а), изобразятся на плоскости в конформной проекции виде кривых (рис. 35, б).

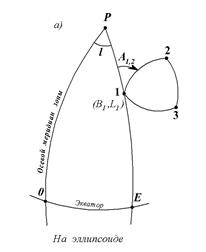
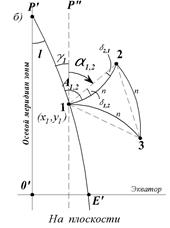
Рис. 35. Изображение линий в конформной проекции Гаусса- Крюгера:

ОР - осевой меридиан зоны, долгота которого равна L₀; Е1Р - геодезический меридиан точки 1, имеющей геодезические координаты B1, L1; l = L₁ - L₀ - долгота точки 1 относительно осевого меридиана; А_1,2 - геодезический азимут линии 1-2; O'P' - осевой меридиан зоны;E'1P' - геодезический меридиан точки 1, имеющей плоские прямоугольные координаты x₁, y₁; α_1,2 - дирекционный угол хорды s_1,2, стягивающей концы изображения стороны треугольника между точками 1 и 2; P"1 - линия, проходящая через точку 1 параллельно осевому меридиану зоны; γ₁ - гауссово сближение меридианов в точке 1.

- 67 -

В связи с тем, что в конформной проекции стороны треугольников изображаются на плоскости кривыми линиями, мы не можем пока применить простые формулы аналитической геометрии для решения геодезических задач. Необходимо криволинейные стороны треугольника на плоскости заменить хордами. Кроме того, надо иметь формулы, позволяющие вычислять с необходимой точностью плоские прямоугольные координаты x, y исходного пункта в точке 1 по его геодезическим координатам - широте В и долготе L. Нужны также формулы для обратного перехода от x, y к B, L в целях контроля правильности преобразования координат из одной системы в другую. Наконец, для вычисления координат x, y других вершин треугольника 1, 2, 3 (рис. 35, б) по наипростейшим формулам

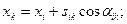
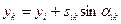(141)

надо определить дирекционные углы α_ik и длины сторон s_ik на плоскости.

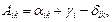Вследствие конформности проекции геодезический азимут на плоскости можно согласно рис. 35, б представить в виде

(142)

где γ_i - гауссово сближении меридианов в i-й точке, α_ik - дирекционный угол хорды ik на плоскости, δ_ik - угол между криволинейной стороной ink на плоскости и её хордой ik.

Отметим, что углы γ, α, δ отсчитываются по ходу часовой стрелки, как положительные величины: угол γ - от изображения меридиана до изображения оси абсцисс x, угол α - от оси x до хорды и угол δ - от криволинейной стороны ink до хорды ik, например, угол δ₁₃ имеет знак плюс, а угол δ₁₂ - знак минус.

Дирекционный угол хорды ik равен

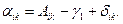(143)

Отсюда видно, что для вычисления дирекционного угла α_ik исходной стороны надо знать Гауссово сближение меридианов γ_i и поправку δ_ik за кривизну изображения стороны треугольника на плоскости в проекции Гаусса - Крюгера или, другими словами, редукцию горизонтального направления.

Наконец, надо иметь формулы для перехода от длины линии S на поверхности земного эллипсоида к проекции этой линии s на плоскости.

- 68 -

Таким образом, для математической обработки геодезических сетей на плоскости в проекции Гаусса - Крюгера необходимо:

1. От геодезических координат исходных пунктов сети перейти к плоским прямоугольным координатам проекции этих пунктов. В целях контроля следует решить обратную задачу: по прямоугольным координатам вычислить геодезические.

2. От исходных длин и геодезических азимутов сторон на поверхности эллипсоида перейти к длинам и дирекционным углам этих сторон на плоскости.

3. Все измеренные направления, редуцированные на поверхность земного эллипсоида, исправить поправками за кривизну изображения сторон на плоскости.

В том случае, когда геодезическая сеть охватывает район двух смежных зон, возникает необходимость преобразования прямоугольных координат из одной зоны в другую.