V. Кривые на поверхности эллипсоида вращения

Взаимные нормальные сечения

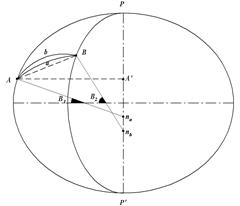Рис. 24. Нормальные сечения

В точках А и В поверхности эллипсоида (рис. 24) с широтами В₁ и В₂ (В₂>В₁) проведём нормали n_a и n_b к поверхности до их пересечения с осью вращения PP'. Нормальные плоскости AaBn_a и AbBn_b образуют с поверхностью эллипсоида кривые АaВ и ВbА, которые называются взаимно обратными нормальными сечениями.

Видно, что несовпадение прямых и обратных нормальных сечений

- 41 -

приводит к тому, что измеренные горизонтальные углы на трёх пунктах треугольника не образуют на поверхности эллипсоида замкнутого треугольника; фигура получается "разорванной". Эту неопределённость в образовании треугольников можно устранить, если вершины соединять геодезическими линиями.

Расхождение взаимных нормальных сечений

а)

б) в)

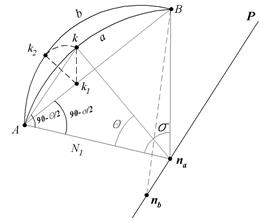
Рис. 25. Расхождение нормальных сечений:

n_a, n_b -точки пересечения нормалей к поверхности эллипсоида в точках А и В с малой осью; σ - угол между прямыми n_aA и n_aB; AaB - прямое нормальное сечение в точке А на точку В; BbA - прямое нормальное сечение в точке В на точку А;

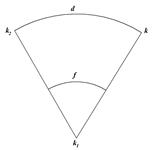
f - угол между плоскостями ABn_a и ABn_b двух взаимно обратных нормальных сечений; d = kk₂ - дуга на поверхности эллипсоида, длина которой равна расстоянию между прямым и обратным нормальными сечениями; АВ - хорда, стягивающая дугу AaB.

- 42 -

Обозначим угол kn_a A - через θ. Угол θ может принимать

значения от 0° до σ . Тогда получим

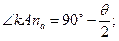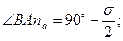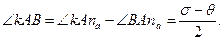
Угол f вычисляют по формуле

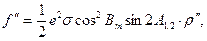(103)

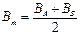где средняя широта отрезка АВ, А _1,2 = А _А,В - азимут

прямого нормального сечения.

Из рис. 25, в следует, что

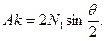(104)

Из треугольника Akk₁ (см. рис. 25-а)

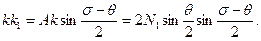(105)

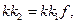Из рис. 25-б имеем

или на основании (103) и (105)

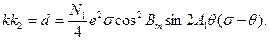(106)

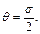Наибольшее линейное расхождение между сечениями AaB и AbB будет в середине дуги АВ, т. е. при

Следовательно, из (106) получаем

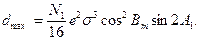(107)

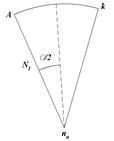
В формуле (107): N₁ - радиус кривизны первого вертикала в точке А;

А₁ - азимут линии АВ.

- 43 -

Пользуясь (107), вычислим значения d_max для различных расстояний s между точками А и В. Положим, что широта В_m = 45°,А₁ = 45°, тогда, получим

s (км) …… 200 100 50

d_max (м) …… 0,050 0,006 0,0008.

Результаты вычислений показывают, что линейные расхождения между прямым и обратным нормальными сечениями малы.

Геодезическая линия

Между двумя точками на любой поверхности можно провести множество кривых.

В геодезии решение задач по определению взаимного положения точек земной поверхности основано на построении на ней определённых фигур (обычно треугольников) и вычислении числовых значений элементов этих фигур. Поэтому следует решить, какими кривыми соединять точки поверхности земного эллипсоида при вычислении элементов геодезических построений.

В сфероидической геодезии точки на поверхности эллипсоида соединяются г е о д е з и ч е с к и м и л и н и я м и, которые определяются как кратчайшие расстояния между ними.

Геодезическая линия на поверхности - такая кривая, в каждой точке которой соприкасающаяся плоскость проходит через нормаль к поверхности в той же точке. Если на поверхности эллипсоида взять три близкие точки M, N, K, через которые провести плоскость,то предельное положение плоскости при M → N и K → N носит название с о п р и -

к а с а ю щ е й с я п л о с к о с т и; касательная в точке N лежит в соприкасающейся плоскости; главная нормаль в точке N совпадает с нормалью к поверхности.

Из определения геодезической линии и понятия соприкасающейся плоскости можно представить следующий геометрический метод построения геодезической линии на поверхности земного эллипсоида.

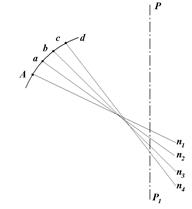
Пусть РР₁ (рис. 26) - малая ось эллипсоида, An₁ - нормаль к поверхности эллипсоида в точке А. Установим в точке А теодолит так, чтобы его ось вращения совпала с нормалью к поверхности эллипсоида в данной точке.

После этого в заданном направлении отметим на поверхности эллипсоида точку а, близкую к точке А. Перенесём теодолит в точку а, совместим ось вращения его с нормалью an₂ к поверхности эллипсоида, наведём трубу на точку А, повернём алидаду горизонтального круга точно на 180° и отметим на поверхности эллипсоида к а точку b. Затем перенесём теодолит в точку b, установим его ось вращения по нормали bn₃, наведём трубу на точку а, повернём алидаду точно на 180° и в коллимационной плоскости наметим точку с, близкую к точке b.

- 44 -

- 44 -

Рис. 26. Пример построения геодезической линии

Поступая таким образом до тех пор, пока расстояние между начальной точкой А и соответствующей точкой i не сделается равным заданному, и предполагая, что указанные выше перестановки теодолита производились через бесконечно малые расстояния, получаем на поверхности эллипсоида

г е о д е з и ч е с к у ю линию (рис. 27).

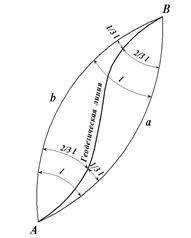Рис. 27. Вид геодезической линии:

AaB - прямое нормальное сечение в точке А; AbB - обратное нормальное сечение в точке А; BbA - прямое нормальное сечение в точке В; BaA - обратное нормальное сечение в точке В.

- 45 -

Геодезическая линия на поверхности эллипсоида (при азимутах, не близких к 90 или 270°) делит угол между взаимными нормальными сечениями в отношении 1:2 и располагается в данной точке ближе к прямому нормальному сечению.

Другими словами, угол между геодезической линией, соединяющей точки

А и В, и прямым нормальным сечением в каждой из этих точек равен 1/3 угла между прямым и обратным нормальными сечениями в данной точке. Эта зависимость используется для получения формулы поправки в направления за переход от прямого нормального сечения к геодезической линии.