IV. Главные радиусы кривизны поверхности эллипсоида в данной точке

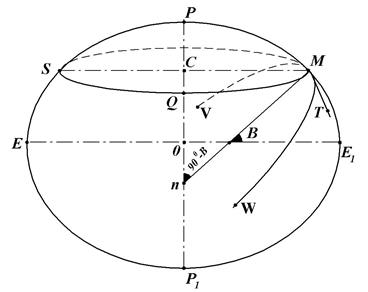Рис. 18. Главные радиусы кривизны эллипсоида

- 25 -

Через нормаль к поверхности эллипсоида можно провести бесчисленное множество плоскостей. Эти плоскости, перпендикулярные к касательной плоскости к поверхности эллипсоида в данной точке, называются нормальными. Кривые, образуемые от пересечения нормальных плоскостей, проведённых в данной точке, с поверхностью эллипсоида, называются нормальными сечениями. В каждой точке существует два взаимно перпендикулярных сечения, кривизна которых имеет наибольшее (максимальное) и наименьшее (минимальное) значения. Эти нормальные сечения называются главными нормальными сечениями.

В некоторой точке М поверхности эллипсоида вращения (рис. 18) главными нормальными сечениями, как известно из дифференциальной геометрии, являются:

1) меридиональное сечение, проходящее через данную точку М и оба полюса эллипсоида Р и Р₁.

2) сечение первого вертикала, проходящее через точку М и перпендикулярное к меридиональному сечению точки М.

Обозначим через M и N радиусы кривизны меридиана и первого вертикала соответственно. Найдём выражения для радиусов кривизны главных нормальных сечений в функции геодезической широты В.

Кривизна любого нормального сечения определяется формулой Эйлера.

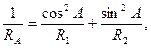(54)

где А- азимут данного нормального сечения, R₁ и R₂ - радиусы кривизны главных нормальных сечений.

§ 11. Радиус кривизны геодезического меридиана и первого вертикала

В данной точке

Радиус кривизны геодезического меридиана в данной точке равен

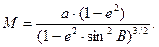(55)

Из (55) ясно, что М возрастает при изменении широты В от 0 до 90°.

- 26 -

Радиус кривизны меридианного эллипса в полюсах (при В = 90°) обозначим через с, тогда

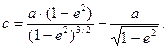(56)

Принимая во внимание, что

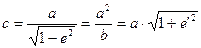
(57)

и обозначив

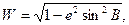(58)

напишем

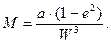(59)

Введём ещё функцию

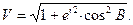(60)

Так как, согласно (13) и (14)

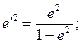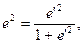то

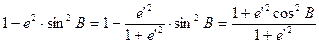
и

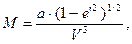(61)

- 27 -

или, согласно (57),

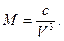(62)

W и V - соответственно называются первой и второй основными функциями геодезической широты В.

Заменяя в (55) первый эксцентриситет его выражением через полуоси эллипсоида и используя обозначения (52), формула (55) для М перепишется

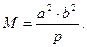
(63)

Для определения радиуса N первого вертикала заметим, что если сечение первого вертикала VMW (рис. 18) - нормальное, то параллель MQS - наклонное сечение, поскольку нормаль не лежит в плоскости этого сечения. Указанные два сечения в точке М имеют общую касательную. Для доказательства этого положения проведём в точке М касательную к параллели МТ; эта касательная, лежащая в плоскости MQSC, перпендикулярной к меридианной плоскости ME₁P₁, перпендикулярна к прямой МС, образованной пересечением этих плоскостей. Таким образом, касательная МТ перпендикулярна к плоскости меридиана РМЕ₁Р₁, поэтому плоскость первого вертикала будет содержать прямую МТ; если Mn - нормаль к поверхности эллипсоида в точке М, то угол TMn равен 90°, следовательно, МТ будет касательной и к кривой EMW.

Имея это в виду, воспользуемся теоремой: если через точку поверхности проведены два сечения - нормальное и наклонное, причём в рассматриваемой точке эти два сечения имеют общую касательную, то радиус кривизны наклонного сечения равен радиусу кривизны нормального сечения, умноженному на косинус угла между плоскостями этих двух сечений.

Из рис. 18 следует, что угол между плоскостями параллели и первого вертикала измеряется углом CMn = B. Поэтому радиус r параллели определится через радиус кривизны первого вертикала N по формуле

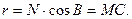(64)

Учитывая выражение (26) для радиуса параллели, получаем

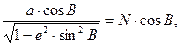(65)

- 28 -

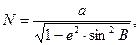откуда (66)

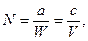или (67)

принимая во внимание обозначение (52), получим

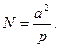(68)

Из рис. 18 следует, что

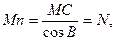(69)

т. е. длина отрезка нормали Mn равна радиусу кривизны первого вертикала.

Радиус кривизны меридиана М служит для вычисления длин дуг меридианов и разностей широт; радиус кривизны первого вертикала N -для вычисления длин дуг параллелей и разностей долгот и азимутов.

Значения радиусов кривизны М и N с ошибкой не более 0,00005 м вычисляются по формулам:

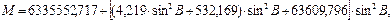(70)

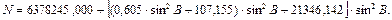(71)

С ошибкой менее 0,2 м главные радиусы кривизны эллипсоида вычисляются по формулам:

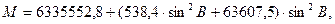(72)

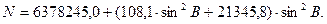(73)