П. 33) Каждая сторона треугольника меньше суммы двух других сторон.

Дано: ∆АВС.

Доказать,что АВ<АС+СВ.

Доказательство:Строим отрезок СМ=ВС на продолжении стороны АС.В равнобедренном ВСМ ∠1 = ∠2 (по свойству углов в равнобедренном треугольнике). ∠1 < ∠АВМ, значит и ∠2 < ∠АВМ.

Рассмотрим треугольник АВМ. Так как в треугольнике против большего угла лежит большая сторона, то АВ<АМ,АВ<АС+СМ,АВ<АС+ВС.

(т.к. СМ = ВС). Ч.т.д.

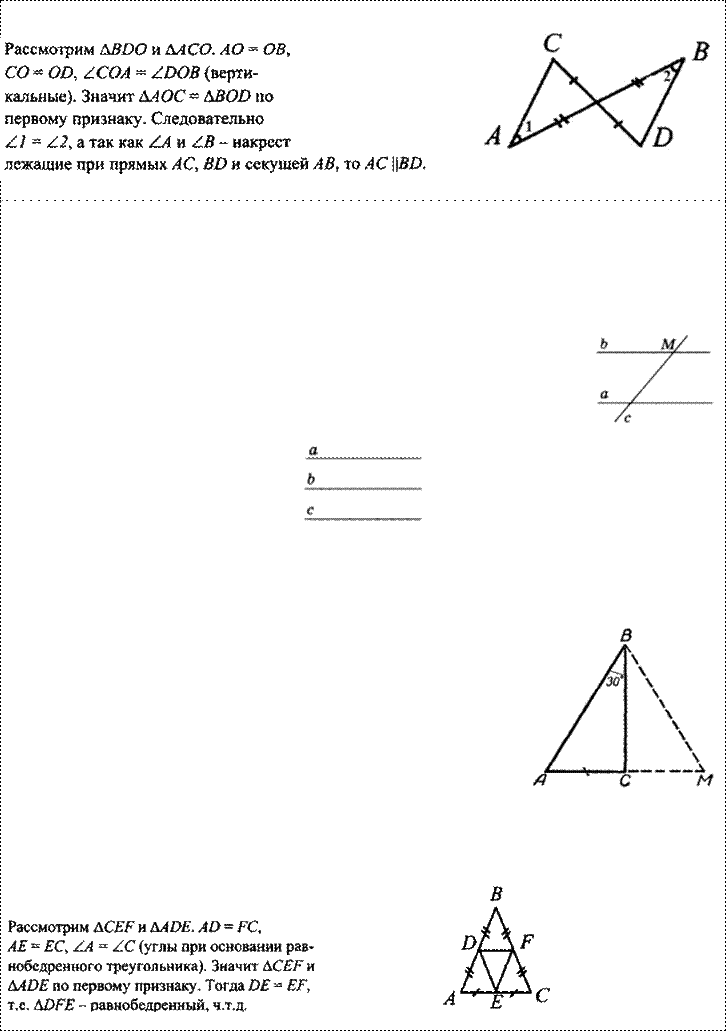3.Отрезки АВ и СDпересекаются в их общей середине.Докажите,что прямые АС и ВDпараллельны.

Доказательство:

О

Билет. 10

1. (п. 27-28) Аксиома–это такая истина,которую не надо доказывать.В каждой науке есть своиаксиомы, на основе которых строят все дальнейшие суждения и доказательства.

Аксиома параллельных прямых:Через данную точку,не лежащую на данной прямой,проходиттолько одна прямая, параллельная данной.

Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Доказательство:Пусть прямая a || b и прямая с пересекает прямую а в точке М.Докажем, что тогда прямая с пересекает и прямую b. Если бы прямая с не пересекала прямую b, то через точку М проходили бы 2 прямые (а и с) параллельные прямой b. Но это противоречит аксиоме параллельных прямых, значит прямая с пересекает прямую b.

Если две различные прямые параллельны третьей прямой, то они параллельны.

2. (п. 34) Свойства прямоугольных треугольников:

1⁰. Сумма двух острых углов в прямоугольном треугольнике равна 90⁰.

Доказательство:В самом деле,сумма углов треугольника равна180⁰,а т.к.прямой угол= 90⁰,тосумма двух других углов в треугольнике = 90⁰.

2⁰. Катет прямоугольного треугольника, лежащий против угла в 30⁰, равен половине гипотенузы.

Доказательство:Пусть в прямоугольном∆АСВ∠В=30°.Тогда другойего острый угол будет равен 60°. Докажем, что катет АС равен половине гипотенузы АВ.

Продолжим катет АС за вершину прямого угла С и отложим отрезок СМ, равный отрезку АС. Точку М соединим с точкой В. Полученный треугольник ВСМ равен треугольнику АСВ. Мы видим, что каждый угол треугольника АВМ равен 60°, следовательно, этот треугольник – равносторонний. Катет АС равен половине AM, а так как AM равняется АВ, то катет АС будет равен половине гипотенузы АВ. Ч.т.д.

3⁰. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30⁰.

3.Доказать,что середины сторон равнобедренного треугольника являются вершинами другогоравнобедренного треугольника.

Доказательство:

Билет. 11

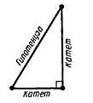
1. (п. 31) Прямоугольный треугольник–это треугольник,у которого один уголпрямой, т.е. равен 90⁰. Сторона, лежащая напротив прямого угла, называется гипотенузой,а две другие стороны-катетами.Гипотенуза всегда большего любого изкатетов, т.к. лежит напротив большего угла в треугольнике.