Экзаменационные билеты по геометрии. 7 класс.

Экзаменационные билеты по геометрии. 7 класс.

Билет №1.

1. Точки. Прямые. Отрезки.

2. Сформулировать и доказать теорему, выражающую третий признак равенства треугольников.

3. Задача на тему «Смежные углы». Найдите величины смежных углов, если один из них в 5 раз больше другого.

Билет №2.

1. Виды треугольников.

2. Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Признаки равенства треугольников». Отрезки AC и BM пересекаются и точкой пересечения делятся пополам. Доказать, что треугольник ABC равен треугольнику CMA.

Билет №3.

1. Линии в треугольнике (медиана, биссектриса, высота).

2. Доказать, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

3. Задача на тему «Окружность». На окружности с центром О отмечены точки А и В так, что угол AOB прямой. Отрезок ВС - диаметр окружности. Докажите, что хорды AB и AC , равны.

Билет №4.

1. Наклонная, проведенная из данной точки к прямой, расстояние от точки до прямой.

2. Доказать, что если при пересечении двух прямых секущей сумма односторонних углов равна 180, то прямые параллельны.

3. Задача на тему «Внешний угол треугольника». Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника.

Билет №5.

1. Определение параллельных прямых, параллельные отрезки.

2. Сформулировать и доказать первый признак равенства треугольников.

3. Задача на тему «Треугольники». В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найти медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см.

Билет №6.

1. Луч Угол. Виды углов.

2. Свойство углов при основании равнобедренного треугольника.

3. Задача на тему «Свойства параллельности двух прямых». Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210°. Найти эти углы.

Билет №7.

1. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей.

2. Сформулировать и доказать теорему, выражающую второй признак равенства треугольников.

Задача на тему «Признаки параллельности двух прямых».

Отрезок АМ-биссектриса треугольника ABC. Через точку M проведена прямая, параллельная AC и пересекающая сторону AB в точке E. Доказать, что треугольник AME равнобедренный.

Билет №8.

1. Объясните, как построить треугольник по двум сторонам и углу между ними.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Второй признак равенства треугольников». На биссектрисе угла А взята точка E, а на сторонах этого угла точки В и С такие, что угол AEC равен углу AEB. Доказать, что BE равно CE.

Билет №9.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Неравенство треугольника.

Задача на тему «Признаки параллельности двух прямых».

Отрезки AB и CD пересекаются в их общей середине. Доказать, что прямые AC и BD параллельны.

Билет №10.

1. Аксиомы геометрии. Аксиома параллельных прямых и свойства из нее вытекающие.

2. Свойства прямоугольных треугольников.

Задача на тему «Соотношения между сторонами и углами треугольника».

Доказать, что середины сторон равнобедренного треугольника являются вершинами другого равнобедренного треугольника.

Билет №11.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Доказать, что при пересечении двух параллельных прямых секущей соответственные углы равны.

3. Задача на тему «Смежные углы».Найти смежные углы, если один из них на 45° больше другого.

Билет №12.

1. Смежные углы ( определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и катету.

Задача на тему «Свойства равнобедренного треугольника».

Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольник равнобедренный.

Билет №13.

1. Вертикальные углы (определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и острому углу.

3. Задача на тему «Признаки равенства треугольников».Отрезки AB и CE пересекаются в их общей середине О. На отрезках AC и BE отмечены точки К и M так, что AK равно BM. Доказать, что OK равно OM.

Билет №14.

1. Объяснить, как отложить на данном луче от его начала отрезок, равный данному.

2. Свойство биссектрисы угла равнобедренного треугольника, проведенной к основанию.

3. Задача на тему «Свойства прямоугольных треугольников».Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетов равна 26,4 см. Найти гипотенузу треугольника.

Билет №15.

1. Какая теорема называется обратной к данной теореме. Привести примеры.

2. Доказать, что если две прямые параллельны третьей, то они параллельны.

3. Задача на тему «Признаки параллельности двух прямых».Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50°. Найти эти углы.

Билет №16.

1. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.

2. Свойство внешнего угла треугольника.

Билет №17

1. Параллельные прямые. Расстояние между параллельными прямыми.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Признаки параллельности двух прямых».В треугольнике ABC угол А равен 40°, а угол ВСЕ, смежный с углом ACB, равен 80°.Доказать, что биссектриса угла ВСЕ параллельна прямой AB.

Билет №18.

1. Признаки равенства прямоугольных треугольников.

2. Доказать свойство вертикальных углов.

3. Задача на тему «Расстояние от точки до прямой».В равнобедренном треугольнике ABC с основанием АС = 37 см, внешний угол при вершине В равен 60°. Найти расстояние от вершины С до прямой AB.

Билет №19.

1. Объяснить, как построить треугольник по трем сторонам. Всегда ли эта задача имеет решение.

2. Доказать, что против большей стороны в треугольнике лежит больший угол.

3. Задача на тему «Периметр треугольника».Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2 см больше периметра другого. Найти боковую сторону данного треугольника.

Билет №20.

1. Объясните, как построить биссектрису данного угла.

2. Доказать, что высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

3. Задача на тему «Свойства прямоугольных треугольников».В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120°, АС + АВ = 18 см. Найти AC и AB.

Билет №21.

1. Объясните, как найти середину отрезка.

2. Доказать, что если при пересечении двух прямых секущей, сумма односторонних углов равна 180, то прямые параллельны.

Билет №22.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Свойства прямоугольных треугольников.

Билет №23.

1. Определение параллельных прямых, параллельные отрезки.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

Билет №24.

1. Виды треугольников.

2.Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Билет №25.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Теорема о сумме углов треугольника.

Билет. 2

1. (п. 14) Треугольник–это геометрическая фигура,состоящая из трех точек,не лежащих на однойпрямой, соединенных отрезками. Точки называются вершинами треугольника, а отрезки – его

сторонами. Виды треугольников:

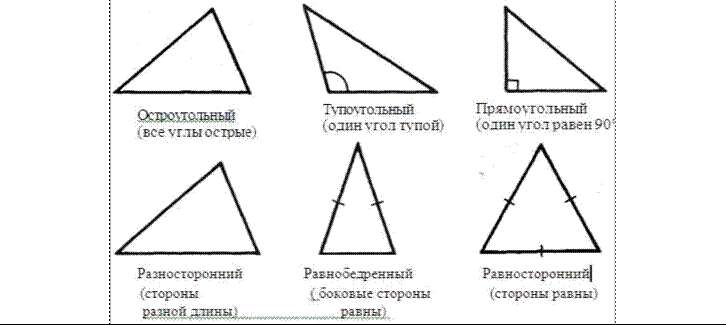
2. (п.25) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

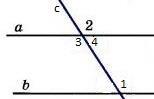Дано:прямые а и b, с –секущая,соответственные углы∠1 =∠2.

Доказать,что а||b

Доказательство:∠1 =∠2 (по условию),∠2 =∠3 (вертикальные),следовательно ∠1 = ∠3, а это накрест лежащие углы, поэтому а||b.

Ч.т.д.

3.Отрезки АС и ВМ пересекаются в точке О и делятся ею пополам.Докажите,что∆АВС= ∆СМА.

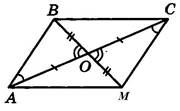Дано:АО=ОС и ВО=ОМ. Доказать,что∆АВС= ∆СМА

Доказательство:Пусть отрезки АС и ВМ пересекаются в точке О.Тогда ∆АОВ = ∆СОМ по I признаку (АО = ОС и ВО = ОМ по условию, а ∠АОВ = ∠СОМ как вертикальные). Следовательно, ∠ВАО = ∠МСО и сторона АВ = МС (в равных треугольниках против равных углов лежат равные стороны).

Тогда ∆АВС = ∆СМА тоже по I признаку (∠ВАО = ∠МСО, АВ = МС, АС – общая сторона). Ч.т.д.

Билет. 3

П.17)

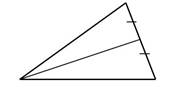
Медиана–это отрезок,идущий из вершинытреугольника к середине противоположной стороны. (Нельзя говорить идущий в противоположную сторону…)

^А1

А

Биссектриса–это отрезок,идущий из вершинытреугольника к противоположной стороне и

делящий угол треугольника пополам.

А₁

30⁰

А 30⁰

Высота–этоперпендикуляр,идущий из вершинытреугольника к противоположной стороне.

(Перпендикуляр – это отрезок, падающий под углом в 90⁰ к прямой).

Высота – это единственная линия в треугольнике, которая при построении может оказаться снаружи треугольника.

В любом треугольнике все 3 медианы пересекаются в одной точке, все 3 биссектрисы пересекаются в одной точке и все 3 высоты пересекаются в одной точке.

Билет. 5

1. (п. 24)Две прямые называютсяпараллельными,если они лежат в однойплоскости и не пересекаются. Обозначение: m || n.

Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой.

Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Все перпендикуляры к одной и той же прямой параллельны между собой.

Два отрезка называются параллельными, если они лежат на параллельных прямых.

2. (п.15) Если 2 стороны и угол между ними одного треугольника соответственно равны 2 сторонам и углу между ними другого треугольника, то такие треугольники равны.

Дано: ∆АВС и∆А₁В₁С₁,у них АВ=А₁В₁,АС=А₁С₁,∠А=∠А₁. Доказать,что∆АВС= ∆А₁В₁С₁

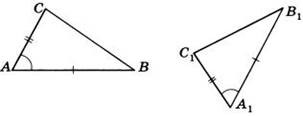
Доказательство:Наложим∆АВС на∆А₁В₁С₁так,чтобывершина А совпала с вершиной А₁. Так как по условию ∠А = ∠А₁, то луч АВ наложится на луч А₁В₁, а луч АС на луч А₁С₁. Еще по условию АВ=А₁В₁, значит точка В совпадет с точкой В₁, АС=А₁С₁, значит точка С совпадет с точкой С₁. Все три точки у треугольников совпали, значит они равны. Ч.т.д.

3.В равнобедренном∆АВС с основанием ВС проведена медиана АМ.Найдите её длину,еслипериметр ∆АВС = 32см, а периметр ∆АВМ равен 24см.

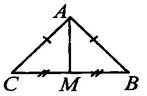Решение:Р_АВС=АВ+ВС+АС

32 = 2АВ+2ВМ (т.к. АВ=АС и ВМ=МС) 32 = 2(АВ + ВМ)

16 = АВ + ВМ.

Р_АВМ = АВ+ВМ+АМ, 24 = 16 + АМ, следовательно АМ = 24 – 16 = 8см.

Ответ:АМ= 8см.

Билет. 6

1. (п. 3-4) Луч(полупрямая) –часть прямой,имеющая начало и не имеющая конца.Угол–это геометрическая фигура,которая состоит из двух лучей исходящих изодной вершины.

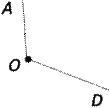
Вершина угла —это точка,в которой два луча берут начало. Стороны угла —это лучи,которые образуют угол.

Например, вершина угла — точка O. Стороны угла — OA и OB. Для обозначения угла в тексте используется символ: ∠AOB.

Способы обозначения углов:

1. Одной заглавной	2. Тремя заглавными латинскими буквами, которыми	3. Двумя строчными
латинской буквой,	обозначены вершина и две точки, расположенные на	латинскими буквами.
указывающейего	сторонах угла. Угол: ∠AOD.	Угол: ∠fn
вершину. Угол: ∠O.
	Называть угол можно с любого края, но НЕ с
	вершины. Угол с рисунка выше имеет два названия:
	∠AOD и ∠DOA.
	Вершина угла должна всегда находиться в середине
	названия!!!

Единица измерения углов — градусы. Углы измеряют с помощью специального прибора – транспортира. Для обозначения градусов в тексте используется символ: °, например ∠В = 50°

Виды углов

Вид угла	Размер в градусах	Пример
Прямой	Равен 90°
Острый	Меньше 90°
Тупой	Больше 90°
Развернутый	Равен 180°

2. (п. 18) В равнобедренном треугольнике углы при основании равны.

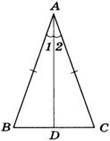Дано: ∆АВС,АВ=АС.

Доказать,что∠В=∠С.

Доказательство:В∆АВС из вершины А проведем биссектрису АД.ТреугольникиABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD – общая сторона, ∠1 = ∠2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠В = ∠С. Ч.т.д.

3.Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна210⁰.Найдите все углы. Решение:

Билет. 7

1. (п. 25)Прямаясназываетсясекущейк прямымаиb,если она пересекает их в двух точках.

При пересечении двух параллельных прямых секущей, образуются восемь углов, которые попарно называются:

1) 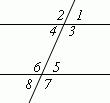соответственные углы (они попарно равны:∠1 =∠5;∠2 =∠6;∠3 =∠7;∠4 =∠8);

2) накрест лежащие углы (4 и 5; 3 и 6);они тоже попарно равны;

3) односторонние углы (3 и 5; 4 и 6);их сумма равна180°

(∠3 + ∠5 = 180°; ∠4 + ∠6 = 180°).

2. (п.19) Если сторона и 2 прилежащих к ней угла одного треугольника соответственно равны стороне и 2 прилежащим к ней углам другого треугольника, то такие треугольники равны.

Дано: ∆АВС и∆А₁В₁С₁,у них АВ=А₁В₁,∠А=∠А₁,∠В=∠В₁ Доказать,что∆АВС= ∆А₁В₁С₁

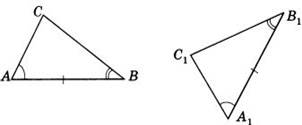
Доказательство:Наложим∆АВС на∆А₁В₁С₁так,чтобысторона АВ совпала со стороной А₁В₁ (по условию они равны, значит совпадут). Так как по условию ∠А = ∠А₁ и ∠В = ∠В₁, то сторона АС наложится на луч А₁С₁, а сторона ВС на луч В₁С ₁. Вершина С окажется лежащей как на луче А₁С₁, так и на луче В₁С₁, а значит совпадет с

вершиной С₁. Все три точки у треугольников совпали, значит они равны. Ч.т.д.

3.АМ–биссектриса∆АВС.Через точку М проведена прямая,параллельная АС и пересекающаясторону АВ в точке Е. Докажите, что ∆АМЕ равнобедренный.

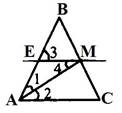
Доказательство:АС||ЕМ,значит∠1 =∠3 (как соответственные углы),∠2 =∠4(как накрест лежащие углы), ∠1 = ∠2 (т.к. АМ – биссектриса).

Следовательно, ∠1 = ∠4, а это углы при основании в ∆АМЕ, значит этот треугольник равнобедренный и АЕ = ЕМ. Ч.т.д.

Билет. 8

1.Постройте треугольник по 2 сторонам и углу между ними. Смотри презентацию, слайд 10.

2. (п. 30) Сумма углов в треугольнике 180⁰.

Дано: ∆АВС.

Доказать,что∠А+∠В+∠С= 180⁰.

Доказательство:Проведем через вершину В прямую а,параллельную стороне АСОчевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е.

∠4 + ∠2 + ∠5 = 180° (*).

Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС.

Поэтому ∠4 = ∠1 = ∠А, ∠5 = ∠3 = ∠С. Отсюда, учитывая равенство (*), получаем: ∠l + ∠2 + ∠3 = 180°,

или ∠A + ∠B + ∠C = 180°. Ч.т.д.

3.На биссектрисе угла А взята точка Е,а на сторонах этого угла точки В и С так,что∠АЕС=∠АЕВ.Докажите, что ВЕ = СЕ.

Доказательство:Рассмотрим∆АСЕ и∆АВЕ.

У них: ∠ВАЕ=∠САЕ, т.к. АЕ – биссектриса угла А, ∠АЕС = ∠АЕВ (по условию). Сторона АЕ – общая.

Значит ∆АСЕ = ∆АВЕ по II признаку. Тогда ВЕ = СЕ. Ч.т.д.

Билет. 9

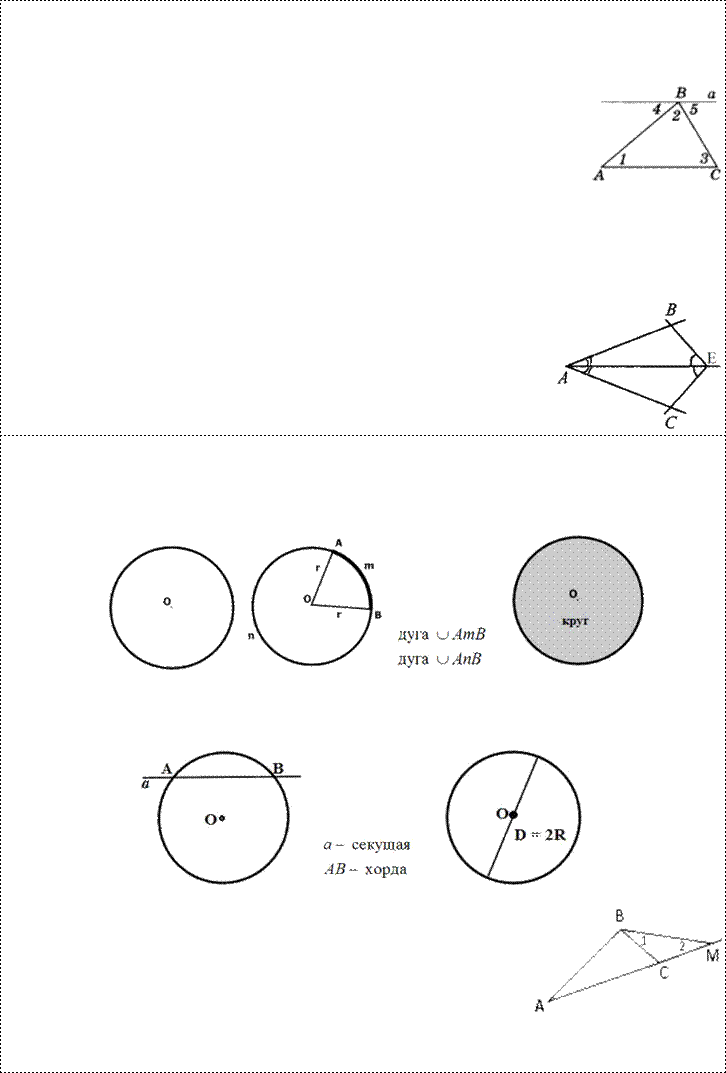
1. (п. 21) Окружность–геометрическое место точек плоскости,равноудаленных от одной ее точки(центра). Равные отрезки, соединяющие центр с любой точкой окружности, называются радиусами. Любые 2 точки окружности делят её на 2 части. Каждая из этих частей называется дугой окружности. Круг–часть плоскости,лежащая внутри окружности.

Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри окружности, - хордой. Хорда – это отрезок, соединяющий 2 точки окружности. Хорда, проходящая через центр окружности, точку О, называется диаметром. Диаметр равен двум радиусам. Для изображения окружности на чертеже пользуются циркулем.

Билет. 10

1. (п. 27-28) Аксиома–это такая истина,которую не надо доказывать.В каждой науке есть своиаксиомы, на основе которых строят все дальнейшие суждения и доказательства.

Аксиома параллельных прямых:Через данную точку,не лежащую на данной прямой,проходиттолько одна прямая, параллельная данной.

Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.

Билет. 12

1. (п. 11) Смежные углы–это два угла,у которых одна сторона общая,	∠1
а две другие являются продолжениями одна другой.	∠2

Свойство: Сумма смежных углов равна 180⁰.

На рисунке ∠1 и ∠2 вместе образуют развернутый угол, а он равен 180⁰, следовательно, ∠1 + ∠2 = 180⁰.

Ч.т.д.

3.Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольник равнобедренный.

Дано:В∆АВС биссектриса ВД–это высота. Доказать,что∆АВС равнобедренный. Доказательство: ∆АВД= ∆СВД по второму признаку

(∠1 =∠2, т.к. ВД – биссек., ∠3 =∠4=90⁰, т.к. ВД – высота, а сторона ВД – общая).

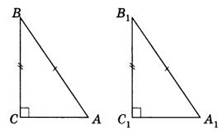
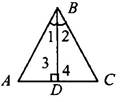Значит АВ = ВС, т.е. ΔABC – равнобедренный. Ч.т.д.

Билет. 13

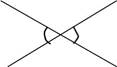
1. (п. 11) Вертикальные углы–это два угла,у которых	стороны одного угла	являются
продолжениями сторон другого.
Теорема: Вертикальные углы равны.
Доказательство:∠1 +∠2 = 1800(смежные),
∠3 + ∠2 = 1800 (смежные),	→ ∠1 = ∠3. Ч.т.д.

Билет. 14

1.Отложить на данном луче от его начала отрезок, равный данному. Смотри презентацию, слайд 2.

Билет. 15

1. (п.29)Во всякой теореме есть2части:условиеизаключение.Условие теоремы–это то,что дано,азаключение – то, что требуется доказать.

Например, рассмотрим теорему: Если 3 стороны первого треугольника соответственно равны 3 сторонам второго треугольника, то такие треугольники равны. В ней условием будет утверждение: 3 стороны первого треугольника соответственно равны 3 сторонам второго треугольника (это дано), а

заключение:треугольники равны(это требуется доказать).

Теоремой, обратной данной,называется такая теорема,в которой условие и заключение меняютсяместами.

Например, для данной выше теоремы обратной теоремой будет: Если треугольники равны, то у них все стороны соответственно равны.

Или для теоремы: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Обратная теорема будет звучать так: Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Билет. 16

1.Как построить треугольник по стороне и двум прилежащим к ней углам. Смотри презентацию,

Слайд 9.

2. (п.30) Внешним углом треугольниканазывается угол,смежный с каким-нибудь углом этоготреугольника.

Свойство: Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Дано: ∆АВС,∠4–внешний.

Доказать,что∠4 =∠1 +∠3.

Доказательство: ∠1 + ∠3 + ∠2 = 180⁰ (по теореме о сумме углов ∆).

∠4 + ∠2 = 180⁰ (смежные)

Следовательно, ∠4 = ∠1 + ∠3. Ч.т.д.

3.Через середину отрезка проведена прямая.Доказать,что концы отрезка равноудалены от этой прямой.Дано:О–середина АВ, l –прямая,проходящая через О.

Доказать,что АА₁=ВВ₁.

Доказательство:АА₁^ l иВВ₁^ l.Рассмотрим прямоугольныетреугольники АОА₁ и ВОВ₁. Они равны по гипотенузе и острому углу (АО = ОВ по условию, ∠1 =∠2, как вертикальные).

Следовательно, АА₁ = ВВ₁. Ч.т.д.

Билет. 17

1. (п.24, 37)Две прямые называютсяпараллельными,если они лежат в одной плоскости и непересекаются. Обозначение: а ǀǀ b.

Два отрезка называются параллельными, если они лежат на параллельных прямых.

Расстоянием от точки до прямой называется длина перпендикуляра,проведенного из этой точки кпрямой.

Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной изпараллельных прямых до другой прямой.

2. (п.32) В треугольнике против большего угла лежит большая сторона.

Дано: ∆АВС,∠С>∠В.

Доказать,что АВ>АС.

Доказательство:Предположим,что это не так.

Тогда либо АВ = АС, либо АВ < АС. В первом случае получаем, что ∆АВС

– равнобедренный, а значит углы при основании равны, т.е. ∠С=∠В, а это противоречит условию, что ∠С > ∠В. Во втором случае получаем, что ∠С < ∠В (т.к. против большей стороны лежит больший угол). Это тоже противоречит условию. Значит, наше предположение неверно, и, следовательно, АВ > АС. Ч.т.д.

3.В∆АВС∠А= 40⁰,а∠ВСЕ смежный с∠АСВ равен80⁰.Доказать,что биссектриса∠ВСЕпараллельна прямой АВ.

Дано:∠А= 40⁰,а∠ВСЕ= 80⁰,СК–биссектриса∠ВСЕ.

Доказать,СКǀǀАВ.

Доказательство:∠ВСК=∠КСЕ=½∠ВСЕ= 80⁰/2 = 40⁰.

Получили, что ∠ВАС = ∠КСЕ = 40⁰, а это соответственные углы при прямых АВ, СК и секущей АС. Раз они равны, то СК ǀǀ АВ. Ч.т.д.

Билет. 18

1. (п.35) Признаки равенства прямоугольных треугольников:

1) по двум катетам:Если два катета одногопрямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.

2) по катету и гипотенузе:Если катет и гипотенуза одногопрямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

3) по гипотенузе и острому углу:Если гипотенуза иострый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

4) по катету и острому углу:Если катет и острый уголодного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

2. (п. 11) Вертикальные углы–это два угла,у которых стороны одного угла являютсяпродолжениями сторон другого.

Теорема: Вертикальные углы равны.
Доказательство:∠1 +∠2 = 1800(смежные),
∠3 + ∠2 = 1800 (смежные),	→ ∠1 = ∠3. Ч.т.д.

3.В равнобедренном∆АВС с основанием АС= 37см,внешний угол при вершине В равен60⁰.Найтирасстояние от вершины С до прямой АВ.

Дано:∆АВС–равнобед.,внешний∠НВС= 60⁰,АС=37см,СН^АВ(т.к.это расстояние).

Найти:длину СН.

Решение:По свойству внешнего угла∠НВС=∠А+∠С= 60⁰.А т.к.∆АВС – равнобед., то ∠А = ∠С = 60⁰/2 = 30⁰ (углы при основании). В прямоугольном треугольнике АНС, ∠А = 30⁰, значит катет лежащий

напротив него равен половине гипотенузы, т.е. СН = ¹₂ АС = 37 : 2 =18,5см. Ответ: СН = 18,5см.

Билет. 19

1.Как построить треугольник по трем сторонам. Смотри презентацию, слайд 8. Задача имеет решение только когда выполняется неравенство треугольника, т.е. сумма двух любых сторон должна быть больше третьей стороны.

2. (п.32) В треугольнике против большей стороны лежит больший угол.

Дано: ∆АВС,АВ>АС.

Доказать,что∠С>∠В

Доказательство:Отложим на стороне АВ отрезокAD=АС.Так какAD <АВ,тоточка D лежит между точками А и В. Следовательно, ∠1 является частью ∠С и, значит, ∠C > ∠1. Угол 2 – внешний угол ∆BDC, поэтому ∠2 > ∠В. ∠1 = ∠2 как углы

при основании равнобедренного треугольника ADC. Таким образом, ∠С > ∠1, ∠1 = ∠2, ∠2 > ∠B. Отсюда следует, что ∠С > ∠В. Ч.т.д.

3.Основание равнобедренного треугольника равно8см.Медиана,проведенная к боковой стороне,разбивает треугольник на два треугольника так, что периметр одного треугольника на 2см больше периметра другого. Найти боковую сторону данного треугольника.

Решение:

Билет. 20

1.Как построить биссектрису данного угла. Смотри презентацию, слайд 4.

Билет. 21

1.Как построить середину отрезка. Смотри презентацию, слайд 7.

2. (п.25) Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰, то прямые параллельны.

Дано:прямые а и b, с –секущая,односторонние углы∠1 +∠4 = 180⁰.

Доказать,что а||b

Доказательство:∠1 +∠4 = 180⁰(по условию),∠3 +∠4 = 180⁰(смежные),следовательно ∠1 = ∠3, а это накрест лежащие углы, поэтому а||b. Ч.т.д.

3.В треугольниках АВС и МКЕ отрезки СО и ЕН медианы,ВС=КЕ,∠В=∠К и∠С=∠Е.Доказать,что∆АСО = ∆МЕН.

Доказательство:По условию:ВС=КЕ,∠В=∠К и∠С=∠Е,значит, ∆АВС = ∆МКЕ (по 2 признаку). Следовательно у этих треугольников равны соответственные стороны и углы, т.е. АВ = МК, а значит и АО = МН, ∠А = ∠М и АС = МЕ. Тогда ∆АСО = ∆МЕН (по 1 признаку).

Билет. 22

1. (п. 21) Окружность–геометрическое место точек плоскости,равноудаленных от одной ее точки(центра). Равные отрезки, соединяющие центр с любой точкой окружности, называются радиусами. Любые 2 точки окружности делят её на 2 части. Каждая из этих частей называется дугой окружности. Круг–часть плоскости,лежащая внутри окружности.

Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри окружности, - хордой. Хорда – это отрезок, соединяющий 2 точки окружности. Хорда, проходящая через центр окружности, точку О, называется диаметром. Диаметр равен двум радиусам. Для изображения окружности на чертеже пользуются циркулем.

2. (п. 34) Свойства прямоугольных треугольников:

1⁰. Сумма двух острых углов в прямоугольном треугольнике равна 90⁰.

Доказательство:В самом деле,сумма углов треугольника равна180⁰,а т.к.прямой угол= 90⁰,тосумма двух других углов в треугольнике = 90⁰.

2⁰. Катет прямоугольного треугольника, лежащий против угла в 30⁰, равен полов