Свойство противолежащих сторон и углов параллелограмма.
| Теорема: У параллелограмма противолежащие стороны равны, противолежащие углы равны | |
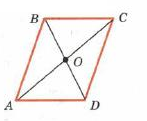 | Дано: АВСD-параллелограмм |
| Док-ть: ВС=АD, АВ=СD, ∟А=∟В=∟С=∟D | |
Доказательство  |
БИЛЕТ№4.
ПОВОРОТ.
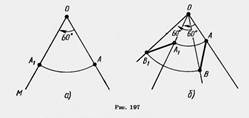 Поворотом на плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении. Поворотом на плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении. 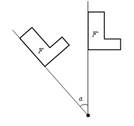 Угол на который поворачивается фигура, относительно точки, называется углом поворота. Угол на который поворачивается фигура, относительно точки, называется углом поворота. |
ПРИЗНАК ПРОТИВОЛЕЖАЩИХ СТОРОН ПАРАЛЛЕЛОГРАММА.
| Теорема: Если у четырехугольника две противолежащие стороны параллельны и равны, то он является паралелограммом | |
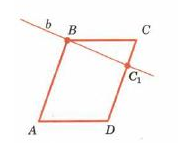 | Дано: АВСD- четырехугольник ВС=АD, АВ=СD, ВС║АD, АВ║СD |
| Док-ть АВСD-. параллелограмм | |
Доказательство  |
БИЛЕТ№5.
СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ.
 Пусть g — фиксированная прямая (рис. 191). Возьмем произвольную точку X и опустим перпендикуляр АХ на прямую g. На продолжении перпендикуляра за точку А отложим отрезок АХ', равный отрезку АХ. Точка X' называется симметричной точке X относительно прямой g. Если точка X лежит на прямой g, то симметричная ей точка есть сама точка X. Очевидно, что точка, симметричная точке Х' есть точка X. Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F' называются симметричными относительно прямой g (рис. 192). Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры. Пусть g — фиксированная прямая (рис. 191). Возьмем произвольную точку X и опустим перпендикуляр АХ на прямую g. На продолжении перпендикуляра за точку А отложим отрезок АХ', равный отрезку АХ. Точка X' называется симметричной точке X относительно прямой g. Если точка X лежит на прямой g, то симметричная ей точка есть сама точка X. Очевидно, что точка, симметричная точке Х' есть точка X. Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F' называются симметричными относительно прямой g (рис. 192). Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры. |
СВОЙСТВО ДИАГОНАЛЕЙ ПРЯМОУГОЛЬНИКА.
| Теорема: Диагонали прямоугольника равны | |
 | Дано: АВСD-прямоугольник |
| Док-ть: АС=BD | |
Доказательство  |
БИЛЕТ №6
СИММЕТРИЯ ОТНОСИТЕЛЬНО ТОЧКИ.
Симметрия относительно точки Пусть О — фиксированная точка и X — произвольная точка плоскости (рис. 187). Отложим на продолжении отрезка ОХ за точку О отрезок ОХ', равный ОХ. Точка X' называется симметричной точке X относительно точки О. Точка, симметричная точке О, есть сама точка О. Очевидно, что точка, симметричная точке X', есть точка X. Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной точки О, называется преобразованием симметрии относительно точки О. При этом фигуры F и F' называются симметричными относительно точки О (рис. 188).  Если преобразование симметрии относительно точки О переводит фигуру F в себя, то она называется центрально-симметричной, а точка О называется центром симметрии. Если преобразование симметрии относительно точки О переводит фигуру F в себя, то она называется центрально-симметричной, а точка О называется центром симметрии. |
ДОКАЖИТЕ, ЧТО ЕСЛИ У ПАРАЛЛЕЛОГРАММА ВСЕ УГЛЫ РАВНЫ, ТО ОН ЯВЛЯЕТСЯ ПРЯМОУГОЛЬНИКОМ.
 | Дано: АВСD- параллелограмм ∟А=∟В=∟С=∟D |
| Док-ть: АВСD-прямоугольник | |
Доказательство  |
БИЛЕТ№7.
1.ОПРЕДЕЛЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОСИНУСА ДЛЯ ЛЮБОГО УГЛА ОТ 0° ДО 180°.
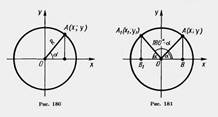 Возьмем окружность на плоскости ху с центром в начале координат и радиусом R (рис. 180). Отложим от положительной полуоси X в верхнюю полуплоскость (полуплоскость, где y>0) угол а. Пусть х и у — координаты точки А. Значения sin а, cos а и tg а для острого угла а выражаются через координаты точки А, а именно: Возьмем окружность на плоскости ху с центром в начале координат и радиусом R (рис. 180). Отложим от положительной полуоси X в верхнюю полуплоскость (полуплоскость, где y>0) угол а. Пусть х и у — координаты точки А. Значения sin а, cos а и tg а для острого угла а выражаются через координаты точки А, а именно: 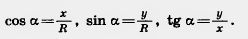 Определим теперь значения sin а, cos а и tg а этими формулами для любого угла а. (Для tg а угол а = 90° исключается.) При таком определении sin 90° = 1, cos 90° = О, sin 180° = О, cos 180° = — 1, tg 180° = 0. Считая, что совпадающие лучи образуют угол 0°, будем иметь: sinO° = 0, cosO° = l, tgO° = 0. Докажем, что для любого угла а, 0°<:а<:180°, sin (180° — а)=sin а, cos (180° — а) = — cos а. Для угла а ^ 90° tg (180° - а) = - tg а. Определим теперь значения sin а, cos а и tg а этими формулами для любого угла а. (Для tg а угол а = 90° исключается.) При таком определении sin 90° = 1, cos 90° = О, sin 180° = О, cos 180° = — 1, tg 180° = 0. Считая, что совпадающие лучи образуют угол 0°, будем иметь: sinO° = 0, cosO° = l, tgO° = 0. Докажем, что для любого угла а, 0°<:а<:180°, sin (180° — а)=sin а, cos (180° — а) = — cos а. Для угла а ^ 90° tg (180° - а) = - tg а. 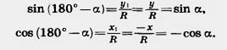 Действительно, треугольники ОАВ и ОА\В\ равны по гипотенузе и острому углу (рис. 181). Из равенства треугольников следует, что АВ=А1В1, т. е. у = у1; ОВ=ОВ1 следовательно, x= —x1. Поэтому разделив почленно равенство sin (180° —а) = sin а на равенство cos (180° — а)=—cos а, получаем: Действительно, треугольники ОАВ и ОА\В\ равны по гипотенузе и острому углу (рис. 181). Из равенства треугольников следует, что АВ=А1В1, т. е. у = у1; ОВ=ОВ1 следовательно, x= —x1. Поэтому разделив почленно равенство sin (180° —а) = sin а на равенство cos (180° — а)=—cos а, получаем: 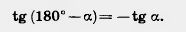 Что и требовалось доказать. Что и требовалось доказать. |
СВОЙСТВА ДИАГОНАЛЕЙ РОМБА.
| Теорема: Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов | |
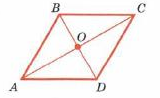 | Дано: АВСD-ромб |
| Док-ть: АС┴BD, АС-биссектриса ∟А и∟С, BD -биссектриса ∟B и∟D | |
Доказательство   |
БИЛЕТ№8.
