Признак диагоналей параллелограмм (доказательство).
| Теорема: Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник — параллелограмм. | |
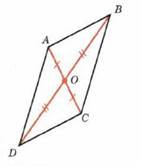 | Дано: АВСD-четырехугольник. АС∩BD=т.О АО=ОС,DО=ОВ |
| Док-ть: АВСD-параллелограмм | |
Доказательство  |
БИЛЕТ№2.
ВЕКТОР. РАВЕНСТВО ВЕКТОРОВ. КООРДИНАТЫ ВЕКТОРА.
Вектор. 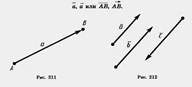 Вектором мы будем называть направленный отрезок. Направление вектора определяется указанием его начала и конца. На чертеже направление вектора отмечается стрелкой. Для обозначения векторов будем пользоваться строчными латинскими буквами a, b, с,. ... . Можно также обозначить вектор указанием его начала и конца. При этом начало вектора ставится на первом месте. Вместо слова «вектор» над буквенным обозначением вектора иногда ставится стрелка или черта. Векторы Вектором мы будем называть направленный отрезок. Направление вектора определяется указанием его начала и конца. На чертеже направление вектора отмечается стрелкой. Для обозначения векторов будем пользоваться строчными латинскими буквами a, b, с,. ... . Можно также обозначить вектор указанием его начала и конца. При этом начало вектора ставится на первом месте. Вместо слова «вектор» над буквенным обозначением вектора иногда ставится стрелка или черта. Векторы 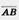 и и 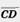 называются одинаково направленными, если полупрямые АВ и CD одинаково направлены. Векторы называются одинаково направленными, если полупрямые АВ и CD одинаково направлены. Векторы 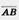 и и 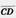 называются противоположно направленными, если полупрямые АВ и CD противоположно направлены. Абсолютной величиной (или модулем) вектора называется длина отрезка,изображающего вектор. Абсолютная величина вектора называются противоположно направленными, если полупрямые АВ и CD противоположно направлены. Абсолютной величиной (или модулем) вектора называется длина отрезка,изображающего вектор. Абсолютная величина вектора 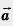 обозначается | обозначается | 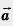 |. Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулем с черточкой |. Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулем с черточкой 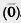 . направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю. . направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю. 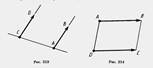 Равенство векторов. Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. Из данного определения равенства векторов следует, что равные векторы одинаково направлены и равны по абсолютной величине. Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны. Координатами вектора Пусть вектор Равенство векторов. Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. Из данного определения равенства векторов следует, что равные векторы одинаково направлены и равны по абсолютной величине. Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны. Координатами вектора Пусть вектор 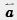 имеет началом точку А1 (х1; у1), а концом — точку А2 (x2; y2). Координатами вектора имеет началом точку А1 (х1; у1), а концом — точку А2 (x2; y2). Координатами вектора 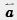 будем называть числа а1=x2 — х1, a2 = y2 — y1. Координаты вектора будем ставить рядом с буквенным обозначением вектора, в данном случае будем называть числа а1=x2 — х1, a2 = y2 — y1. Координаты вектора будем ставить рядом с буквенным обозначением вектора, в данном случае 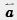 (а1;а2) или просто (а1;а2) или просто 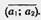 . Координаты нулевого вектора равны нулю. Из формулы, выражающей расстояние между двумя точками через их координаты, следует, что абсолютная величина вектора с координатами a1, a2 равна . Координаты нулевого вектора равны нулю. Из формулы, выражающей расстояние между двумя точками через их координаты, следует, что абсолютная величина вектора с координатами a1, a2 равна 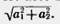 . Равные векторы имеют равные соответствующие координаты. И обратно: если у векторов соответствующие координаты равны, то векторы равны. . Равные векторы имеют равные соответствующие координаты. И обратно: если у векторов соответствующие координаты равны, то векторы равны. |
СВОЙСТВА ДИАГОНАЛЕЙ ПАРАЛЛЕЛОГРАММА.
| Теорема: Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам | |
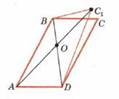 | Дано: АВСD-параллелограмм |
| Док-ть АС∩BD=т.О АО=ОС,DО=ОВ | |
 Доказательство Доказательство |
БИЛЕТ №3.
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС.
Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние. Определение Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F. 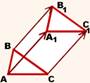 Формулы параллельного переноса Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1) Формулы параллельного переноса Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1) 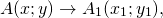 то параллельный перенос задаётся формулами: то параллельный перенос задаётся формулами: 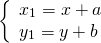 Свойства параллельного переноса 1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние). 2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. 3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя). 4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1. В алгебре параллельный перенос широко используется для построения графиков функций. Свойства параллельного переноса 1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние). 2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. 3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя). 4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1. В алгебре параллельный перенос широко используется для построения графиков функций. |
