Свойства медиан треугольника

№ 1.1 (из учебника Л.С. Атанасяна №404)

Медиана, проведенная к гипотенузе, равна половине гипотенузы.

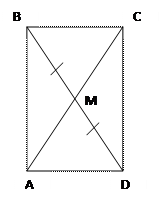
Дано: ∆АВD – прямоугольный, ∟А=90 ͦ, АМ – медиана, ВМ=МD

Доказать: АМ=ВМ=1/2ВD

Доказательство: т.к. ∆АВD – прямоугольный, то мы можем достроить его до прямоугольника АВСD. Диагонали прямоугольника мочкой пересечения делятся пополам, значит, АВ=МС и ВМ=МD, но в прямоугольнике диагонали равны → АМ=ВМ=1/2ВD ч.т.д.

№ 1.2(из учебника Л.С. Атанасяна №110)

Если медиана является высотой, то треугольник равнобедренный.

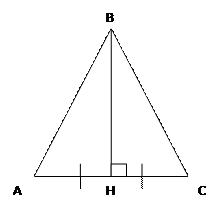Дано: ∆АВС, АН=НС, ∟ВНС=90 ̊, ВН – медиана и высота.

Доказать: ∆АВС – равнобедренный.

Доказательство: рассмотрим ∆АВН и ∆ВНС в них: АН=НС и ∟ВНА=∟ВНС=90 ͦ (по условию) ВН – общая → ∆ равны по 1ПРТ. Значит, АВ=ВС, как соответственные стороны равных ∆→ ∆АВС – равнобедренный ч.т.д.

№ 1.3 (из учебника Л.С. Атанасяна №114)

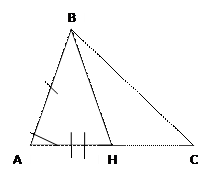В равных треугольниках медианы, проведённые к соответствующим сторонам равны.

Дано: ∆АВС=∆А₁В₁С₁, ВН и В₁Н₁ - медианы, АН=НС, А₁Н₁=Н₁С₁

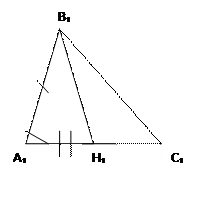Доказать: ВН=В₁Н₁

Доказательство: рассмотрим ∆АВН и ∆А₁В₁Н₁ в них: ∟А=∟А₁ и АВ=А₁В₁ т.к. ∆АВС=∆А₁В₁С₁, АН=А₁Н₁, потому что АС=А₁С₁. Значит, ∆АВН=∆А₁В₁С₁ по I ПРТ → ВН=В₁Н₁ как соответственные стороны равных ∆ ч.т.д.

№ 1.4(из учебника Л.С. Атанасяна №611)

Медиана делит пополам любой отрезок, параллельной стороне, к которой проведена эта медиана.

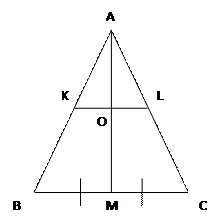Дано: ∆АВС, АМ – медиана, КL ǁ‖BC, К є АВ, LєAC

Доказать: КО=ОL

Доказательство: рассмотрим ∆АОLи ∆АМС: ∟А – общий, ∟АLO=∟ACM(как соответственные при КLǁBCи АС – секущая) → ∆подобны по 2 углам.

OL/MC=AO/АМ; OL=AO*MC/АМ

∆АКО~∆АВМ аналогично.

ОК=ВМ*АО/АМ, а т.к. ВМ=МС (по условию), то ОК=OLч.т.д.

№ 1.5(из учебника Л.С. Атанасяна №624)

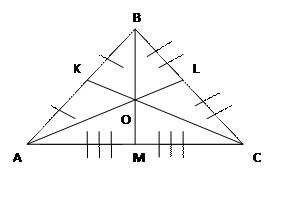Медианы треугольника разбивают его 6 треугольников, площади которых попарно равны.

Дано: ∆АВС; ВМ, КС, АL–медианы

Доказать: S∆ABM=S∆BMC, S∆AKC=S∆BKC, S∆АВL=S∆ALC

Доказательство: S∆ABM=1/2ВН*АМ; S∆BMC=1/2ВН*МС, а т.к. ВМ – медиана и АМ=МС то S∆ABM=S∆BMC. S∆AKC=S∆BKC и S∆ABL=S∆ALC – аналогично ч.т.д.

2.Свойства биссектрис треугольника

№ 2.1(из учебника Л.С. Атанасяна №128)

В равных треугольниках биссектрисы, проведённые к соответственно равным сторонам, равны.

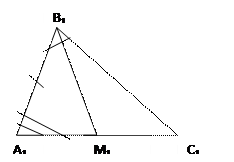Дано: ∆АВС=∆А₁В₁С₁, ∟АВМ=∟МВС, ∟А₁В₁М₁=∟М₁В₁С₁, ВМ и В₁М₁ - биссектрисы

Доказать: ВМ=В₁М₁

Доказательство: рассмотрим ∆АВМ и ∆А₁В₁М₁ в них: ∟А=∟А₁ и АВ=А₁В₁, т.к. ∆АВМ=∆А₁В₁С₁. ∟АВМ=∟А₁В₁М₁, потому что ∟В=∟В₁ ( по условию) → ∆АВМ=∆А₁В₁М₁ по II ПРТ. Значит, ВМ=В₁М₁, как соответственные стороны равных ∆ ч.т.д.

№ 2.2(из учебника Л.С. Атанасяна №133)

Если биссектриса треугольника является его высотой, то треугольник равнобедренный.

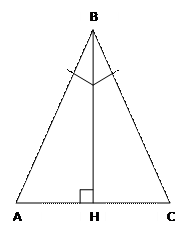Дано: ∆АВС, ВН – высота и биссектриса, ∟АВН=∟НВС, ∟АНВ=∟ВНС=90 ͦ

Доказать: ∆АВС – равнобедренный

Доказательство: рассмотрим ∆АВН и ∆НВС в них: ∟АВН=∟НВС и ∟АНВ=∟ВНС=90 ͦ (по условию), ВН – общая → ∆АВН=∆НВС. Значит, АВ=ВС, как соответственные стороны равных ∆ ч.т.д.

№ 2.3 (из учебника Л.С. Атанасяна №242)

Если биссектриса внешнего угла треугольника параллельна стороне треугольника, то треугольник равнобедренный.

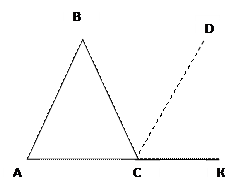Дано: СD – биссектриса, CD ǁ‖ АВ

Доказать: ∆АВС – равнобедренный

Доказательство: ∟DCK=∟САВ, т.к. DC ǁ‖ АВ. ∟АВС=∟ВСD, при АВ ‖ǁ CDиBC – секущей (как накрест лежащие углы). Раз ∟DCK=∟САВ, то и ∟ВCD=∟САВ, потому что CD – биссектриса, значит, ∟АВС=∟САВ=∟ВСD → ∆АВС – равнобедренный с основанием АВ ч.т.д.

№ 2.4

Биссектриса угла треугольника делит противоположенную сторону на части, пропорциональные прилежащим сторонам треугольника.

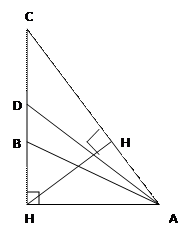Дано: ∆АВС, АD — биссектриса

Доказать: АС/СD=АВ/ВD

Доказательство: ∆ABDи ∆АСD имеют общую высоту AH, поэтому S∆ABD/S∆ACD=BD/СD. С другой стороны, эти же ∆ имеют по равному углу (∟DAB=∟DAC), поэтому S∆ABD/S∆ACD=AB*AD/АС*АD=AB/АС. Из двух равенств для отношения площадей получаем BD/СD=AB/АС, или BD/АВ=СD/АС ч.т.д.

№ 2.5

Биссектриса параллелограмма отсекает от него равнобедренный треугольник.

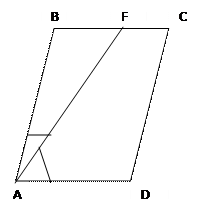Дано: ABCD — параллелограмм, AF — биссектриса ∟BAD, Fє BC.

Доказать: ∆ ABF — равнобедренный.

Доказательство: ∟BAF=∟DAF (так как AF — биссектриса ∟BAD по условию);∟BFA=∟DAF (как внутренние накрест лежащие углы при BC ‖ǁ AD и секущей AF), значит, ∟BAF=∟BFA →∆ABF — равнобедренный с основанием AF (по признаку), значит, AB=BF ч.т.д.

Свойства высот треугольник

№ 3.1 (из учебника Л.С. Атанасяна №274)

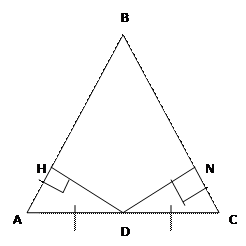
Дано: ∆АВС – равнобедренный, АD=DC,

HD AB и DN BC

Доказать: НD=DN

Доказательство: рассмотрим ∆АНD и ∆DNC в них: AD=DC, ∟A=∟C (по условию), значит, ∆ равны по гипотенузе и прилежащему углу ведь ∆ прямоугольные → HD=DN как соответственные стороны равных ∆ ч.т.д.

№ 3.2 (из учебника Л.С. Атанасяна №307)

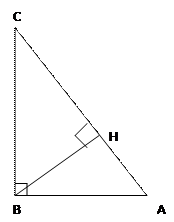Дано: ∆АВС – прямоугольный, ∟В=90 ͦ, ВН – высота

Доказать: ∆АВС, ∆АВН, ∆ВНС имеют соответственные равные углы

Доказательство: введём обозначения ∟ВАС=1, ∟АВН=2, ∟НВС=3, ∟ВСА=4.

∟1+∟4=90 ͦ т.к. ∆АВС – прямоугольный. ∟4+∟3=90 ͦ т.к. ∆ВНС – прямоугольный, значит, ∟1=∟3, аналогично, ∟4=∟2.

Имеем: ∟ВНА=∟ВНС=∟АВС=90 ͦ; ∟1(в ∆АВН)=∟1(в ∆АВС )= =∟3; ∟2=∟4(в ∆ВНС)=∟4(в ∆АВС) ч.т.д.

№ 3.3 (из учебника Л.С. Атанасяна №310)

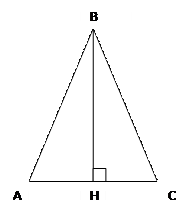В равных треугольниках высоты, проведённые к равным сторонам, равны.

Дано: ∆АВС=∆А₁В₁С₁, ВН и В₁Н₁ - высоты

Доказать: ВН=В₁Н₁

Доказательство: рассмотрим ∆АВН и ∆А₁В₁Н₁: ∟А₁=∟А и АВ=А₁В₁, т.к. ∆АВС=∆А₁В₁С₁ (по условию), ∆АВН и ∆А₁В₁Н₁ - прямоугольные → ∆АВН=∆А₁В₁Н₁ (по гипотенузе и углу). Значит, ВН=В₁Н₁ ч.т.д.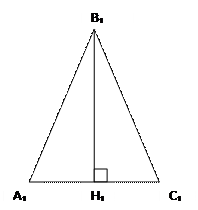

№ 3.4 (из учебника Л.С. Атанасяна №532)

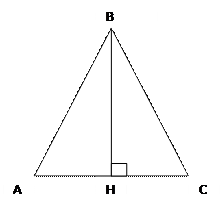Дано: ∆АВС, ВН – высота

Доказать: ВС²=АВ²+АС²─2АВ*АН

Доказательство: ∟А – острый. ∆ВНС – прямоугольный: ВС²=ВН²+НС²; НС²=(АС─АН)²; из ∆АВН ВН²=АВ²─АН²; ВС²=(АС─АН)²+АВ²─АН²=АС²─2АС*АН+ +АН²+АВ²─АН²=АС²+АВ²─2АС*АН ч.т.д.

Свойства элементов трапеции

№ 4.1

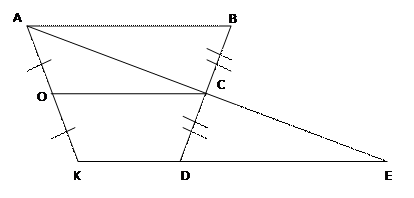
Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.

Дано: ОС — средняя линия трапеции АВDК, т. е. ОК = ОА и ВС = СD.

Доказать: 1) ОС || КD и ОС || АВ;

2) OC=(KD+AB)/2

Доказательство. Через точки А и С проведём прямую, пересекающую продолжение основания КD в некоторой точке Е.

В треугольниках АBС и DСЕ:

ВС = СD — по условию;

∟ACB = ∟DCE, как вертикальные,

∟CDE = ∟ABC, как внутренние накрест лежащие при параллельных АВ и KЕ и секущей ВD. Следовательно, ∆ АBС = ∆ DСЕ. Отсюда АС = СЕ, т.е. ОС является средней линией треугольника КАЕ.

1) ОС || КЕ и, значит, ОС || КD и ОС || AВ;

2)ОС=КЕ/2=(КD+DE)/2 , но DЕ = АВ (из равенства треугольников АBС и DСЕ), поэтому отрезок DЕ можно заменить равным ему отрезком АВ. Тогда получим: ОС=(KD+AB)/2 ч.т.д.

№ 4.2 (из учебника Л.С. Атанасяна№386)

Отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.

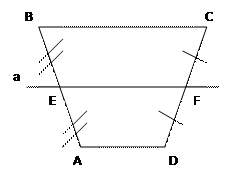Дано: АВСD – трапеция, ВЕ=ЕА, СF=FD

Доказать: EFBC и EF ‖ǁ AD

Доказательство: через точку Е проведём прямую а такую, что а ǁ‖ ВС и а ‖ǁ АD. По теореме Фалеса а пересечёт СD по середине, то есть в точке F и EF будет ǁ‖ ВС и ǁ‖ АD ч.т.д.

№ 4.3 (из учебника Л.С. Атанасяна №388)

В равнобедренной трапеции углы при основаниях равны и равны диагонали.

Дано: АВСD – равнобедренная трапеция, АС и ВD – диагонали

Доказать: а) ∟А=∟D и ∟В=∟С; б) АС=ВD

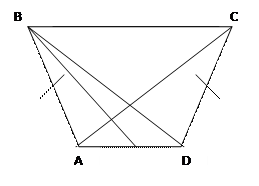Доказательство: а) проведём прямую ВЕ такую, что ВЕǁ‖СD и точка Е є АD. Имеем: ЕВСD – параллелограмм, СD=ВЕ и СD=AB → АВ=ВЕ, значит, ∆АВЕ – равнобедренный. ∟А=∟ВЕА, ∟ВЕD+∟CDE=180 ͦ (как углы парал-мм.) ∟ВЕD+∟BEA=180 ͦ (как смежные углы).

Значит, ∟ВЕА=∟CDE=∟BAE → ∟A=∟D и ∟В=∟С (аналогично) ч.т.д.

б) Рассмотрим ∆АВD и ∆DCA: AD – общая, ∟A=∟D, АВ=СD → ∆ равны по углу и 2 сторонам, значит, АС=ВD (как соответственные стороны равных ∆) ч.т.д.

№ 4.4 (из учебника Л.С. Атанасяна №389)

Если углы равны при основании и равны диагонали, то трапеция равнобедренная. (Обратная задача к №4.3)

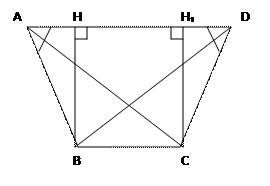
Дано: АВСD – трапеция, ∟А=∟D, АС=ВD

Доказать: АВСD – равнобедренная трапеция

Доказательство: ∟А=∟Dи ∟В=∟C. Проведём высоты из углов В и С к основанию АD, ВН и СН₁. Имеем ∆АВН и ∆СDН₁ в них: ВН=СН₁ (т.к. ВСНН₁ - прямоугольник), ∟Н=∟Н₁=90 ͦ и ∟А=∟D(по условию), значит, ∆АВН=∆СDН₁ по катету и острому углу → АВ=СD→АВСD–равнобедренная трапеция ч.т.д.

№ 4.5 (из учебника Л.С. Атанасяна №569)

Отрезок, соединяющий середины диагоналей, равен полуразности оснований.

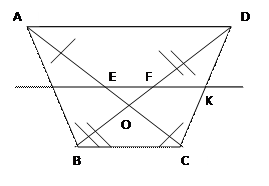
Дано: АВСD – трапеция, АС и ВD–диагонали, точка Е є АС, точка FєBD, АЕ=ЕС, BF=FD

Доказать: EF ‖ǁ BCи ЕF ǁ‖ АD, EF=1/2(АD─BC)

Доказательство: через точку Е проведём прямую ЕК (точка К є СD) такую, что ЕК ‖ǁ АDи ЕК ‖ǁ ВС.

Рассмотрим ∆АСD: АЕ=ЕС и ЕК ‖ǁ АD, значит, ЕК – средняя линия → ЕК=1/2АD, аналогично FK=1/2BC. EK=EF+FK. EF=EK-FK=1/2(AD-BC) ч.т.д.

№ 4.6 (из учебника Л.С. Атанасяна №833)

Площадь трапеции равна произведению длины боковой стороны и перпендикуляра, опущенного на эту боковую сторону.

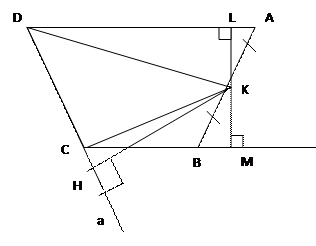Дано: АВСD – трапеция, КН – перпендикуляр к DC, ВК=КА, точка К є АВ

Доказать: SABCD=CD*KH

Доказательство: SABCD=S∆KCD+S∆KBC+S∆AKD.

Проведём высоту МLчерез точку К.

S∆AKD=1/2KL*AD; S∆KDC=1/2КМ*ВС; МК=КLт.к. ∆МВК=∆АКL(по гипотенузе и прилежащему углу)

S∆AKD+S∆KBC=1/2KL*AD+1/2KL*BC=

=1/2KL(AD+BC)

SABCD=1/2ML(AD+BC), т.к. ML=2KL, то S∆AKD+S∆KBC=1/2SABCD

S∆KCD=1/2SABCD=1/2KH*DC

SABCD=2S∆KCD=KH*DC ч.т.д.