Понятие площади и её измерение.

Понятие о площади фигуры имеет любой человек: мы говорим о площади комнаты, площади земельного участка, о площади поверхности, которую надо покрасить, и так далее. При этом мы понимаем, что если земельные участки одинаковы, то площади их равны; что у большего участка площадь больше; что площадь квартиры слагается из площади комнат и площади других её помещений.

Это обыденное представление о площади используется при её определении в геометрии, где говорят о площади фигуры. Но геометрические фигуры устроены по-разному, и поэтому когда говорят о площади, выделяют особый класс фигур. Например, рассматривают площади многоугольников и других ограниченных выпуклых фигур, или площадь круга, или площадь поверхности тел вращения и так далее. В начальном курсе математики рассматриваются только площади многоугольников и ограниченных выпуклых плоских фигур. Такая фигура может быть составлена из других. Например, фигура F, (рис.4), составлена из фигур F1, F2, F3. Говоря, что фигура составлена (состоит) из фигур F1, F2,…,Fn, имеют в виду, что она является их объединением и любые две данные фигуры не имеют общих внутренних точек. Площадью фигуры называется неотрицательная величина, определённая для каждой фигуры так, что:

I/ равные фигуры имеют равные площади;

2/ если фигура составлена из конечного числа фигур, тоеёплощадь равна сумме их площадей. Если сравнить данное определение с определением длины отрезка, то увидим, что площадь характеризуется теми же свойствами, что и длина, но заданы они на разных множествах: длина - на множестве отрезков, а площадь - на множестве плоских фигур. Площадь фигуры F обозначать S(F). Чтобы измерить площадь фигуры, нужно иметь единицу площади. Как правило, за единицу площади принимают площадь квадрата со стороной, равной единичному отрезку e, то есть отрезку, выбранному в качестве единицы длины. Площадь квадрата со стороной e обозначают e . Например, если длина стороны единичного квадрата m, то его площадь m .

Измерение площади состоит в сравнении площади данной фигуры с площадью единичного квадрата e. Результатом этого сравнения является такое число x, что S(F)=x e .Число x называют численным значением площади при выбранной единице площади.

Площадь многоугольника.

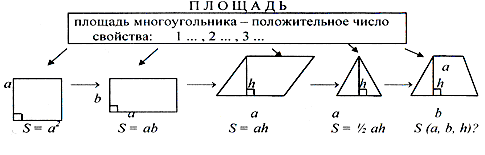
Площадь произвольной плоской фигуры и её измерение.

Формулы площади треугольника

1. Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

S =		a · h

2. Формула площади треугольника по трем сторонам

Формула Герона

S = √p(p - a)(p - b)(p - c)

3. Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S =		a · b · sin γ

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности

S =	a · b · с
4R

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

S = p · r

Формулы площади квадрата

1. Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.

S = a²

2. Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.

S =		d2

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b

Формулы площади параллелограмма

1. Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h

2. Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

S = a · b · sin α

3. Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма

S =		d1d2 sin γ

Формулы площади ромба

1. Формула площади ромба по длине стороны и высоте
S = a · h

2. Формула площади ромба по длине стороны и углу
S = a² · sin α

3. Формула площади ромба по длинам его диагоналей

S =		d1 · d2

1. Формула Герона для трапеции

S =	a + b	√(p - a)(p - b)(p - a - c)(p - a - d)
|a - b|

2. Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту

S =		(a + b) · h