Деление отрезка прямой в данном отношении
Точка делит отрезок прямой линии в пространстве в таком же отношении, в каком проекции точки делят одноименные с ними проекции отрезка (рис. 24).
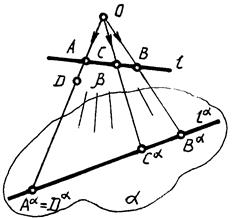
| Рис. 24 |
Так, например, надо разделить отрезок АВ в отношении 2:3, делящая точка лежит на отрезке (рис. 24).
По основному положению мы должны иметь:
КА/КВ = К'А'/К'В' = К''В''/К''В'' = 2/3
На чертеже сначала определяем горизонтальную проекцию К' точки, которая делит горизонтальную проекцию А'В' данного отрезка АВ в отношении 2:3. Для этого через точку А' проводим произвольную прямую, на которой от точки А' отложим пять равных произвольных отрезков (2+3=5). Далее соединяем прямой линией точки 5 и В' и проводим прямую 2К, параллельную прямой 5В'. Точка К' разделит отрезок А'В' в отношении 2:3. Проведя линию связи, находим фронтальную проекцию К'' искомой точки К. Точка К'' разделит отрезок А''В'' в отношении К''А''/К''В'' = 2/3.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
План:
4.1. Параллельные прямые
4.2. Пересекающиеся прямые
4.3. Скрещивающиеся прямые
Параллельные прямые
Если провести через данные параллельные прямые АВ и СD плоскости, перпендикулярные горизонтальной плоскости проекций, то эти две плоскости будут параллельны, и в их пересечении с плоскостью H будут получены две взаимно параллельные прямые A'B' и C'D', являющиеся ортогональными проекциями данных прямых АВ и CD на горизонтальную плоскость проекций (рис. 25).
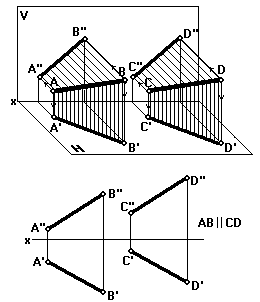
| Рис. 25 |
Аналогичным образом можно получить и ортогональные проекции данных прямых на фронтальную плоскость V.
На комплексном чертеже одноименные проекции параллельных прямых параллельны: A'B' C'D' и A''B'' C''D'' (рис. 25).
Пересекающиеся прямые
Взаимно пересекающиеся прямые имеют общую точку, например, отрезки прямых АВ и CD пересекаются в точке К. Проекции пересекающихся прямых пересекаются, и точки их пересечения (K' и K'') лежат на одной линии связи — перпендикуляре к оси x (рис. 26).
Скрещивающиеся прямые
Это прямые, которые не параллельны и не пересекаются. На комплексном чертеже проекции скрещивающихся прямых (прямые АВ и CD) могут пересекаться, но точки пересечения (1,2 и 3,4) лежат на разных линиях связи (рис. 27). Точкам пересечения одноименных проекций скрещивающихся прямых соответствуют в пространстве две точки: в одном случае — 1 и 2, а в другом — 3 и 4, расположенные на прямых. На чертеже точке пересечения горизонтальных проекций прямых соответствует две фронтальные проекции точек 1'' и 2''. Аналогично — с точками 3 и 4.
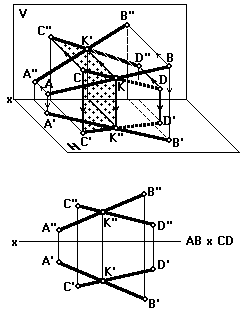 |
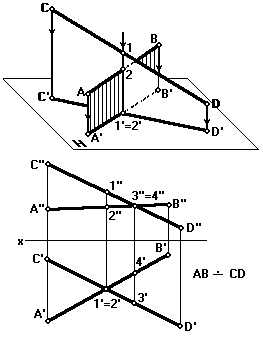
| Рис. 26 Рис. 27 |
5. ПЛОСКОСТЬ
План:
5.1. Проекции плоскостей общего положения
5.2. Проекции плоскостей уровня
Горизонтальная плоскость
Фронтальная плоскость
Профильная плоскость
5.3. Проекции проецирующих плоскостей
Горизонтально-проецирующая плоскость
Фронтально-проецирующая плоскость
Профильно-проецирующая плоскость
5.4. Взаимное расположение двух плоскостей
Параллельные плоскости
Пересекающиеся плоскости
5.5. Пересечение плоскостей общего положения
5.6. Взаиморасположение прямой и плоскости
Прямая - в плоскости
Прямая, параллельная плоскости
Прямая пересекает плоскость
5.7. Пересечение прямой с плоскостью
5.8. Условие видимости на чертеже
