На какое минимальное количество лет можно взять кредит при условии, что ежегодные платежи были не более 350000 рублей?

Решение: Очевидно, что наименьший срок кредитования сложится при условии ежегодной выплаты максимальной выплаты, т.е. 350000 рублей.

1. 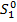=S+0,1*S-Х=1300000+130000-350000=1080000

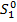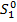2. = +0,1* -X=1080000+108000-350000=838000

3. = +0,1* -X=838000+83800-350000=571800

4. = +0,1* -X=571800+51800-350000=279980

И, следовательно, на пятый год кредитования оставшаяся сумма погасится полностью.

Ответ: 5

Задача №3.2

В июле планируется взять кредит на сумму 16 млн. рублей на некоторый срок (целое число лет). Условия возврата таковы:

· 1-го числа каждого месяца долг возрастает на 25% по сравнению с предыдущего года;

· С февраля по июнь каждого месяца необходимо выплатить часть долга;

· В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

На сколько лет планируется взять кредит, если известно, что выплаченная за весь срок кредитования сумма выплат составит 38 млн. рублей?

Решение:

Пусть кредит взят на N лет. Тогда ежегодно равномерно выплачиваемая сумма равна 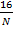. Тогда сумма полного погашения складывается из:

S_вып=S+0,25* 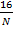.*(N+(N-1)+(N-2)+….+1)=16+0,25* 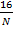.*( *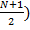N

38=16+2*N+2. Следовательно, N=10

Ответ: 10

Тип. Применение задач с помощью математического анализа.

Задача №4.1

Зависимость объема Q (в шт) купленного у фирмы товара от цены P (руб за шт)выражается формулой: Q=15000-Р, где 1000≤Р≤15000. Доход от продажи товара составляет Q*Р рублей. Затраты на производство Q единиц товара составляют

3000* Q+5000000. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену продукции на 20%, однако ее прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?

Решение:

Пусть D- доход от продажи, r-искомый процент увеличения сниженной цены, Z- затраты на производство, Y- предполагаемая прибыль, P- цена товара, Q - объем закупленного товара.

Тогда прибыль равна Y=D-Z=P*Q-3000*Q-5000000=P(15000-P)- 3000*(15000-P)-5000000= (15000-P)(P-3000)+5000000.Нам необходимо узнать первоначальную цену. Ее будем искать из условия, что прибыль не изменяется при снижении цены на 20%. Тогда Y=Y_сн и потому (15000-P)(P-3000)+5000000=(15000-0,8*P)(0,8*P-3000)+5000000.Произведя необходимые вычисления, получим: 0,36*Р=3600 и Р=10000 рублей.

Теперь повысив цену Р_cн на r%, получим:

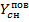=((15000-0,8* (1+ )*P)(0,8* (1+ )*P-3000)-5000000.Произведя вычисления, получим 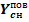=(15000-0,8* (1+ )*Р)( 0,8* (1+ )*Р-3000-5000000

Так как Р- переменная величина (1000≤Р≤15000),то прибыль 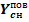рассмотрим как функцию от переменной Р и получим: =(15000-0,8* (1+ )*10000)( 0,8* (1+ )*10000-3000)-5000000. Найдем производную от :

ⁱ=(-0,8* (1+ )*10000)( 0,8* (1+ )*10000-3000)+ (15000-0,8* (1+ )*10000)* 0,8* (1+ )*10000. ⁱ=0

15000-0,8* (1+ )*10000 - 0,8* (1+ )*10000+3000=0.Разделив обе части на 1000, получим:18-1,6*(1+ )*10=0.Произведя вычисления, получим: 200=16*r.Отсюда,r=12,5%

Ответ:12,5

Задача №4.2

Строительство нового завода стоит 75 млн. рублей. Затраты на Х тыс. единиц продукции на таком заводе равны 0,5*Х²+Х+7 млн. рублей в год. Если продукцию завода продать по цене Р тыс. рублей за единицу, то прибыль фирмы (в млн. руб) за один год составит Р*Х-(0,5*Х²+Х+7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении Р строительство завода окупится не более, чем за 3 года?

Решение:

Пусть Y=Р*Х-(0,5*Х²+Х+7). Следовательно, Р*Х=25+0,5*Х²+Х+7. Тогда Р=(32+0,5*Х²+Х)/Х. Рассмотрев цену продукцию как функцию от затрат Х, получим:

Р(Х) =(32+0,5*Х²+Х)/Х. Тогда (Р(Х))ⁱ=((Х+1)*Х-(32+0,5*Х²+Х)*1)/Х². (Р(Х))ⁱ=0

(Х+1)*Х-(32+0,5*Х²+Х)=0. Следовательно, 0,5*Х²=32. Очевидно, что Х=8 тыс. ед

Вычислим Р=(32+0,5*64+8)/8=9 тыс. рублей.

Ответ: 9

Задачи для самостоятельного решения

Типы экономических задач: