Известно, что восьмая выплата составила 108 тыс. рублей. Какую сумму нужно выплатить банку в течение всего срока кредитования?

Решение:

1. Анализ. Пусть ежемесячные выплаты по кредиту (без процентов) составляют Хрублей. Тогда сумма кредита составит составляет 15Хрублей (без процентов). Процентная ставка р%составляет 1% или 0,01.

Найти: S-сумму выплаты кредита в течении всего срока

S=15Х+(15Х+14Х+13Х+….+Х)*0.01=15Х+ 15*0.01*(15Х+Х)/2)=15Х+1,2Х=16,2Х

Необходимо найти Х.

2. Поиск математической модели решения задачи:

Пусть Р₈– сумма, которую составляют проценты на восьмой месяц кредитования.

Тогда по условию задачи восьмая выплата будет равна: 108 000 = Х + Р₈,

За восемь месяцев сумма кредита составит 8Х руб.

На восьмой месяц проценты составят Р₈ = 8Х*0,01 = 0,08Х (руб.).

Тогда 108 000 = Х + 0,08Х;

Решение математической модели: 108 000 = 1,08Х;

Х = 100 000 (руб.) составляет сумма ежемесячных выплат (без процентов).

Сумма кредита составляет 100 000*15 =1 500 000(руб.)

3) Следовательно, S=16,2*X=16,2*1000000=1620000 (руб)

Ответ: 1620 000

Задача № 1.3

Сергей взял кредит на срок 9 месяцев. В конце каждого общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

Решение: Пусть Х- ежемесячно выплачиваемая сумма. Тогда S=9*X – сумма взята Сергеем в кредит. С другой стороны, S_вып= 9*Х+ (9*Х+Х)/2*9*0.12=9*Х+5.4*Х=14.4*Х. Составим пропорцию:

9*Х – 100%

14.4*Х - У%

Тогда У%=(14.4*100)/9=160%. Следовательно, сумма, уплаченная Сергеем банку, составит 60% от суммы кредита, взятого Сергеем в банке.

Ответ:60

Задача №1. 4

Иван взял кредит в банке на 5 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 10%, а затем уменьшаетсяна сумму уплаченную Иваном. Суммы, выплачиваемые Иваном в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. За весь срок кредитования Иван выплатил банку в общей сложности 16250 рублей. Какую сумму он взял в банке в кредит?

Решение:

Пусть X- равномерно выплачиваемая ежемесячная выплата. Тогда S=5*Х. Вся сумма выплаченная за период кредитования равна: S_вып=5*Х+(5*Х+Х)/2*5*0.1=6,5*Х. По условию задачи 6,5*Х=16250. Следовательно, Х=2500 рублей. И сумма, полученная в кредит, равна: 2500*5=12500

Ответ:12500

Задача №5

В июле планируется взять кредит в банке на сумму 28 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:

· Каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

· С февраля по июнь каждого года необходимо выплатить часть долга;

· В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит 9 млн. рублей?

Решение:

1. =S+0,25*S=35 – долг на конец июня. Мы знаем, что наибольшая выплата Х₁=9

2. 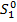=35-9=26 – остаток долга на конец первого года. Ясно, что 28-26=2. Таким образом

3. =26+26*0,25=32,5

4. =26-2=24. Следовательно, вторая выплата Х₂=8,5

5. =24+24*0,25=30

6. =24-2=22. Таким образом, третья выплата Х₃=8

7. _i≥2 и =9+8,5+8+7,5+7+6,5+6+5,5+5+4,5+4+3,5+3+2,5=80,5 млн. рублей

ответ:80500000