Тип. Определение суммы кредита

Немного теории

Сначала рассмотрим так называемые «банковские» задачи: варианты, когда имеет дело с вкладом и кредиты.

Рассмотрим вариант, когда мы вкладываем деньги в банк на N лет некоторую сумму S под r% годовых.

1. Через год имеем на счету S₁= S+r/100* S=(1+r/100) S

2. Через два года на счету будет S₂=(1+r/100)* S +((1+r/100)*S)*r/100=((1+r/100)*S)(1+r/100)=(1+r/100)²*S

3. Продолжая аналогичную схему рассуждения получим:

S_n=(1+r/100)ⁿ*S - (1)

Для более компактной записи формулы (1) введем замену переменной q=(1+r/100)и формула (1) примет вид: S_n =qⁿ *S (2)

Рассмотрим вариант, когда мы берем кредит в банке на N лет некоторую сумму S под r% годовых.

1. К концу 1 года, наш долг увеличился на заявленные банком проценты, а мы платим заявленный платеж. Пусть Х- ежегодный платеж. Долг наш будет иметь следующий вид: 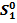=S+r*S-X=(1+r)*S-X=q*S-X

2. Через год долг будет: 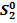= (q*S-X)+(q*S-X)*r-X=(q*S-X)(1+r)-X= (q*S-X)*q-X=q²*S-q*X-X=q²*S-(1+q)X

3. Аналогично продолжая рассуждения получим, что к концу договора мы полностью выплачиваем кредит и 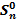=qⁿ*S-(1+q)^n-1*X.Так как кредит выплачен полностью, то

qⁿ*S-(1+q+q²+….+q^n-1)*X =qⁿ*S-(1+q)^n-1*X=0.Следовательно, qⁿ*S=(1+q)^n-1*X. qⁿ*S-(1+q)^n-1*X.Домножив и разделив правую часть на (q-1)получим:

qⁿ*S= 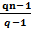*X (3)

Для облегчения решения задач предлагаю воспользоваться следующими формулами, которые можете доказать самостоятельно:

1. Если величину х увеличить на р % , то получим х·(1+р/100)

2. Если величину х уменьшить на р % , то получим х·(1-р/100)

3. Если величину х увеличить на р %, а затем уменьшить на q %, то получим х·(1+р/100)(1-q/100)

4. Если величину х увеличить дважды на р%, получим х·(1+р/100)²

5. Если величину х уменьшить дважды на р%, получим х·(1-р/100)²

Тип. Определение суммы кредита

Задача 1.1

31 декабря 2014 года Василий взял в банке некоторую сумму в кредит под 11% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 11%), затем Василий переводит в банк 3696300 рублей. Какую сумму Василий взял в кредит в банке, если он выплатил долг двумя платежами (т.е. за 2 года)?

Решение:

1 способ:

Пусть S- сумма кредита, Х- выплачиваемая сумма, r- процентная ставка и Х=3696300 рублей, r=11% или r=0,11, n=2.

Тогда q²*S=(q²-1)/(q-1)*X. Следовательно, S=((q+1)*X)/q². Получим, что Василий взял в кредит 6330000 рублей. Ответ:6330000

2 способ:

1. К концу первого года мы имеем долг: 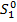=S+0.11*S –Х=1.11*S-X

2.Через год остаток после выплаты будет: 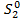=(1.11*S-X)+(1.11*S-X)*0.11-X=(1.11*S-X)*1.11-X=1.11²*S-2.11*X. Так как Василий выплатил долг за два транша, то 1.11²*S-2.11*X=0. Решив полученное уравнение, имеем: S=2.11*3696300/1,2321=6330000 рублей.

Ответ: 6330000

Задача № 1.2

15 января планируется взять в кредит в банке на 15 месяцев. Условия его возврата таковы:

– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;

– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Ответ: 1620 000

Задача № 1.3

Сергей взял кредит на срок 9 месяцев. В конце каждого общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

Решение: Пусть Х- ежемесячно выплачиваемая сумма. Тогда S=9*X – сумма взята Сергеем в кредит. С другой стороны, S_вып= 9*Х+ (9*Х+Х)/2*9*0.12=9*Х+5.4*Х=14.4*Х. Составим пропорцию:

9*Х – 100%

14.4*Х - У%

Тогда У%=(14.4*100)/9=160%. Следовательно, сумма, уплаченная Сергеем банку, составит 60% от суммы кредита, взятого Сергеем в банке.

Ответ:60

Задача №1. 4

Иван взял кредит в банке на 5 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 10%, а затем уменьшаетсяна сумму уплаченную Иваном. Суммы, выплачиваемые Иваном в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. За весь срок кредитования Иван выплатил банку в общей сложности 16250 рублей. Какую сумму он взял в банке в кредит?

Решение:

Пусть X- равномерно выплачиваемая ежемесячная выплата. Тогда S=5*Х. Вся сумма выплаченная за период кредитования равна: S_вып=5*Х+(5*Х+Х)/2*5*0.1=6,5*Х. По условию задачи 6,5*Х=16250. Следовательно, Х=2500 рублей. И сумма, полученная в кредит, равна: 2500*5=12500

Ответ:12500

Задача №5

В июле планируется взять кредит в банке на сумму 28 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:

· Каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

· С февраля по июнь каждого года необходимо выплатить часть долга;

· В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

Задача 2.1

15 января планируется взять кредит1,8 млн. рублей в банке на 24 месяца. Условия его возврата таковы:

- 1-го числа последующего месяца долг возрастает на r% по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число месяца необходимо выплатить часть долга;

- 15-го числа каждого месяца, последующего за месяцем получения кредита, долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Суммы, выплачиваемые Иваном, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Найдите r, если за первые шесть месяцев Иван выплатил банку 740250 рублей?

Решение:

Пусть S=1800000 рублей – сумма кредита, Х- ежемесячно равномерно выплачиваемая сумма, r%- процентная ставка банка. Очевидно, что Х=1800000/24=75000 рублей.

1. Тогда 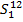_вып=6*Х+(24*X+23*X+22*X+21*X+20*Х+19*Х)*0,01*r. Тогда r%=(740250-450000)/1,29*75000=3

Ответ:3

Задача №2.2

15 января планируется взять кредит в банке на два года. Условия его возврата таковы:

- 1-го числа последующего месяца долг возрастает на r% по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число месяца необходимо выплатить часть долга;

- 15-го числа каждого месяца, последующего за месяцем получения кредита, долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r%.

Решение: Пусть S-сумма кредита в банке, Х- ежемесячно равномерно выплачиваемая сумма, r%- процентная ставка банка, известно также, что S_вып=24*Х+(24Х+23Х+…+Х)*24*0,01*r. Следовательно, S_вып=24*Х+3*Х*r_. По условию задачи,

S_вып=24*Х+3*Х*r - 125%

S=24*X - 100%

Произведя арифметические действия, получим: 3*r=6. Тогда, r%=2%

Ответ: 2

Задача №2.3

В июле планируется взять кредит на сумму 4,5 млн. рублей на срок 9 лет. Условия возврата таковы:

· 1-го числа каждого месяца долг возрастает на r% по сравнению с предыдущего года;

· С февраля по июнь каждого месяца необходимо выплатить часть долга;

· В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

Найдите r%, если известно, что наибольший годовой платеж по кредиту составит не более 1,4 млн. рублей, а наименьший – не менее 0,6 млн. рублей.

Решение:

1. Пусть X- сумма ежемесячного равномерно вносимого платежа и она равна: Х=4500000/9=500000 рублей.

2. Теперь разберемся из чего складывается наибольшая сумма платежа: Х_наиб≥500000+0,01*r*4500000 (1)

3. Теперь разберемся из чего складывается наименьшая сумма платежа: Х_наим≤500000+0,01*r*500000 (2)

4. Решив неравенства (1) и (2), получим: 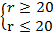. Следовательно, возможно только r=20

Ответ: 20

Задача №3.1

В июле планируется взять кредит в банке на сумму 1300000 рублей на некоторый срок (целое число лет). Условия его возврата таковы:

· 1-го числа каждого месяца долг возрастает на 10% по сравнению с предыдущего года;

· С февраля по июнь каждого месяца необходимо выплатить часть долга;

· В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

Задача №3.2

В июле планируется взять кредит на сумму 16 млн. рублей на некоторый срок (целое число лет). Условия возврата таковы:

· 1-го числа каждого месяца долг возрастает на 25% по сравнению с предыдущего года;

· С февраля по июнь каждого месяца необходимо выплатить часть долга;

· В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

На сколько лет планируется взять кредит, если известно, что выплаченная за весь срок кредитования сумма выплат составит 38 млн. рублей?

Решение:

Пусть кредит взят на N лет. Тогда ежегодно равномерно выплачиваемая сумма равна 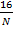. Тогда сумма полного погашения складывается из:

S_вып=S+0,25* 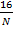.*(N+(N-1)+(N-2)+….+1)=16+0,25* 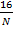.*( *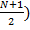N

38=16+2*N+2. Следовательно, N=10

Ответ: 10

Задача №4.1

Зависимость объема Q (в шт) купленного у фирмы товара от цены P (руб за шт)выражается формулой: Q=15000-Р, где 1000≤Р≤15000. Доход от продажи товара составляет Q*Р рублей. Затраты на производство Q единиц товара составляют

3000* Q+5000000. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену продукции на 20%, однако ее прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?

Решение:

Пусть D- доход от продажи, r-искомый процент увеличения сниженной цены, Z- затраты на производство, Y- предполагаемая прибыль, P- цена товара, Q - объем закупленного товара.

Тогда прибыль равна Y=D-Z=P*Q-3000*Q-5000000=P(15000-P)- 3000*(15000-P)-5000000= (15000-P)(P-3000)+5000000.Нам необходимо узнать первоначальную цену. Ее будем искать из условия, что прибыль не изменяется при снижении цены на 20%. Тогда Y=Y_сн и потому (15000-P)(P-3000)+5000000=(15000-0,8*P)(0,8*P-3000)+5000000.Произведя необходимые вычисления, получим: 0,36*Р=3600 и Р=10000 рублей.

Теперь повысив цену Р_cн на r%, получим:

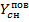=((15000-0,8* (1+ )*P)(0,8* (1+ )*P-3000)-5000000.Произведя вычисления, получим 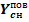=(15000-0,8* (1+ )*Р)( 0,8* (1+ )*Р-3000-5000000

Так как Р- переменная величина (1000≤Р≤15000),то прибыль 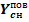рассмотрим как функцию от переменной Р и получим: =(15000-0,8* (1+ )*10000)( 0,8* (1+ )*10000-3000)-5000000. Найдем производную от :

ⁱ=(-0,8* (1+ )*10000)( 0,8* (1+ )*10000-3000)+ (15000-0,8* (1+ )*10000)* 0,8* (1+ )*10000. ⁱ=0

15000-0,8* (1+ )*10000 - 0,8* (1+ )*10000+3000=0.Разделив обе части на 1000, получим:18-1,6*(1+ )*10=0.Произведя вычисления, получим: 200=16*r.Отсюда,r=12,5%

Ответ:12,5

Задача №4.2

Строительство нового завода стоит 75 млн. рублей. Затраты на Х тыс. единиц продукции на таком заводе равны 0,5*Х²+Х+7 млн. рублей в год. Если продукцию завода продать по цене Р тыс. рублей за единицу, то прибыль фирмы (в млн. руб) за один год составит Р*Х-(0,5*Х²+Х+7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении Р строительство завода окупится не более, чем за 3 года?

Решение:

Пусть Y=Р*Х-(0,5*Х²+Х+7). Следовательно, Р*Х=25+0,5*Х²+Х+7. Тогда Р=(32+0,5*Х²+Х)/Х. Рассмотрев цену продукцию как функцию от затрат Х, получим:

Р(Х) =(32+0,5*Х²+Х)/Х. Тогда (Р(Х))ⁱ=((Х+1)*Х-(32+0,5*Х²+Х)*1)/Х². (Р(Х))ⁱ=0

(Х+1)*Х-(32+0,5*Х²+Х)=0. Следовательно, 0,5*Х²=32. Очевидно, что Х=8 тыс. ед

Вычислим Р=(32+0,5*64+8)/8=9 тыс. рублей.

Ответ: 9

Задачи для самостоятельного решения

Типы экономических задач:

VI. Другие задачи

Предлагаю Вам самостоятельно:

1. Определить тип задачи и выбрать метод решения

2. Построение математической модели и получение результата.

1.1 июня 2013 года Все­во­лод Яро­сла­во­вич взял в банке 900000 руб­лей в кре­дит. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая — 1 числа каж­до­го сле­ду­ю­ще­го ме­ся­ца банк на­чис­ля­ет 1 про­цент на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 1%), затем Все­во­лод Яро­сла­во­вич пе­ре­во­дит в банк платёж. На какое ми­ни­маль­ное ко­ли­че­ство ме­ся­цев Все­во­лод Яро­сла­во­вич может взять кре­дит, чтобы еже­ме­сяч­ные вы­пла­ты были не более 300000 руб­лей?

2.Алек­сей при­обрёл цен­ную бу­ма­гу за 8 тыс. руб­лей. Цена бу­ма­ги каж­дый год воз­рас­та­ет на 1 тыс. руб­лей. В любой мо­мент Алек­сей может про­дать бу­ма­гу и по­ло­жить вы­ру­чен­ные день­ги на бан­ков­ский счёт. Каж­дый год сумма на счёте будет уве­ли­чи­вать­ся на 8%. В те­че­ние ка­ко­го года после по­куп­ки Алек­сей дол­жен про­дать цен­ную бу­ма­гу, чтобы через два­дцать пять лет после по­куп­ки этой бу­ма­ги сумма на бан­ков­ском счёте была наи­боль­шей?

3. 15-го ян­ва­ря пла­ни­ру­ет­ся взять кре­дит в банке на 19 ме­ся­цев. Усло­вия его воз­вра­та та­ко­вы:

— 1-го числа каж­до­го ме­ся­ца долг воз­растёт на r% по срав­не­нию с кон­цом преды­ду­ще­го ме­ся­ца;

— со 2-го по 14-е число каж­до­го ме­ся­ца не­об­хо­ди­мо вы­пла­тить часть долга;

— 15-го числа каж­до­го ме­ся­ца долг дол­жен быть на одну и ту же сумму мень­ше долга на 15-е число преды­ду­ще­го ме­ся­ца. Из­вест­но, что общая сумма вы­плат после пол­но­го по­га­ше­ния кре­ди­та 30% боль­ше суммы, взя­той в кре­дит. Най­ди­те r.

4. 31 де­каб­ря 2014 года Ти­мо­фей взял в банке 7 007 000 руб­лей в кре­дит под 20% го­до­вых. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая: 31 де­каб­ря каж­до­го сле­ду­ю­ще­го года банк на­чис­ля­ет про­цен­ты на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 20%), затем Ти­мо­фей пе­ре­во­дит в банк платёж. Весь долг Ти­мо­фей вы­пла­тил за 3 рав­ных пла­те­жа. На сколь­ко руб­лей мень­ше он бы отдал банку, если бы смог вы­пла­тить долг за 2 рав­ных пла­те­жа?

5. Са­ве­лий хочет взять в кре­дит 1,4 млн руб­лей. По­га­ше­ние кре­ди­та про­ис­хо­дит раз в год рав­ны­ми сум­ма­ми (кроме, может быть, по­след­ней) после на­чис­ле­ния про­цен­тов. Став­ка про­цен­та 10% го­до­вых. На какое ми­ни­маль­ное ко­ли­че­ство лет может Са­ве­лий взять кре­дит, чтобы еже­год­ные вы­пла­ты были не более 330 тысяч руб­лей?

6.Алек­сей взял кре­дит в банке на срок 12 ме­ся­цев. По до­го­во­ру Алек­сей дол­жен вер­нуть кре­дит еже­ме­сяч­ны­ми пла­те­жа­ми. В конце каж­до­го ме­ся­ца к остав­шей­ся сумме долга до­бав­ля­ет­ся r % этой суммы и своим еже­ме­сяч­ным пла­те­жом Алек­сей по­га­ша­ет эти до­бав­лен­ные про­цен­ты и умень­ша­ет сумму долга. Еже­ме­сяч­ные пла­те­жи под­би­ра­ют­ся так, чтобы долг умень­шал­ся на одну и ту же ве­ли­чи­ну каж­дый месяц (на прак­ти­ке такая схема на­зы­ва­ет­ся «схе­мой с диф­фе­рен­ци­ро­ван­ны­ми пла­те­жа­ми»). Из­вест­но, что общая сумма, вы­пла­чен­ная Алек­се­ем банку за весь срок кре­ди­то­ва­ния, ока­за­лась на 13 % боль­ше, чем сумма, взя­тая им в кре­дит. Най­ди­те r.

7. 15-го ян­ва­ря пла­ни­ру­ет­ся взять кре­дит в банке на 39 ме­ся­цев. Усло­вия его воз­вра­та та­ко­вы:

— 1-го числа каж­до­го ме­ся­ца долг воз­растёт на r% по срав­не­нию с кон­цом преды­ду­ще­го ме­ся­ца;

— со 2-го по 14-е число каж­до­го ме­ся­ца не­об­хо­ди­мо вы­пла­тить часть долга;

— 15-го числа каж­до­го ме­ся­ца долг дол­жен быть на одну и ту же сумму мень­ше долга на 15-е число преды­ду­ще­го ме­ся­ца. Из­вест­но, что общая сумма вы­плат после пол­но­го по­га­ше­ния кре­ди­та на 20% боль­ше суммы, взя­той в кре­дит. Най­ди­те r.

8. Из­вест­но, что вклад, на­хо­дя­щий­ся в банке с на­ча­ла года, воз­рас­та­ет к концу года на опре­де­лен­ный про­цент, свой для каж­до­го банка. В на­ча­ле года Сте­пан по­ло­жил 60% не­ко­то­рой суммы денег в пер­вый банк, а остав­шу­ю­ся часть суммы во вто­рой банк. К концу года сумма этих вкла­дов стала равна 590 000 руб., а к концу сле­ду­ю­ще­го года 701 000 руб. Если бы Сте­пан пер­во­на­чаль­но по­ло­жил 60% своей суммы во вто­рой банк, а остав­шу­ю­ся часть в пер­вый, то по ис­те­че­нии од­но­го года сумма вкла­дов стала бы рав­ной 610 000 руб. Ка­ко­ва была бы сумма вкла­дов в этом слу­чае к концу вто­ро­го года?

9. Граж­да­нин Пет­ров по слу­чаю рож­де­ния сына от­крыл 1 сен­тяб­ря 2008 года в банке счёт, на ко­то­рый он еже­год­но кла­дет 1000 руб­лей. По усло­ви­ям вкла­да банк еже­год­но на­чис­ля­ет 20% на сумму, на­хо­дя­щу­ю­ся на счёте. Через 6 лет у граж­да­ни­на Пет­ро­ва ро­ди­лась дочь, и 1 сен­тяб­ря 2014 года он от­крыл в дру­гом банке счёт, на ко­то­рый еже­год­но кладёт по 2200 руб­лей, а банк на­чис­ля­ет 44% в год. В каком году после оче­ред­но­го по­пол­не­ния суммы вкла­дов срав­ня­ют­ся, если день­ги со сче­тов не сни­ма­ют?

10.В на­ча­ле года 5/6 не­ко­то­рой суммы денег вло­жи­ли в банк А, а то, что оста­лось — в банк Б. Если вклад на­хо­дит­ся в банке с на­ча­ла года, то к концу года он воз­рас­та­ет на опре­делённый про­цент, ве­ли­чи­на ко­то­ро­го за­ви­сит от банка. Из­вест­но, что к концу пер­во­го года сумма вкла­дов стала равна 670 у.е., к концу сле­ду­ю­ще­го — 749 у.е. Если пер­во­на­чаль­но 5/6 суммы было бы вло­же­но в банк Б, а остав­шу­ю­ся вло­жи­ли бы в банк А, то по ис­те­че­нии од­но­го года сумма вы­рос­ла бы до 710 у.е. Опре­де­ли­те сумму вкла­дов по ис­те­че­нии вто­ро­го года в этом слу­чае.

11. Алек­сей взял кре­дит в банке на срок 17 ме­ся­цев. По до­го­во­ру Алек­сей дол­жен вер­нуть кре­дит еже­ме­сяч­ны­ми пла­те­жа­ми. В конце каж­до­го ме­ся­ца к остав­шей­ся сумме долга до­бав­ля­ет­ся r % этой суммы и своим еже­ме­сяч­ным пла­те­жом Алек­сей по­га­ша­ет эти до­бав­лен­ные про­цен­ты и умень­ша­ет сумму долга. Еже­ме­сяч­ные пла­те­жи под­би­ра­ют­ся так, чтобы долг умень­шал­ся на одну и ту же ве­ли­чи­ну каж­дый месяц (на прак­ти­ке такая схема на­зы­ва­ет­ся «схе­мой с диф­фе­рен­ци­ро­ван­ны­ми пла­те­жа­ми»). Из­вест­но, что общая сумма, вы­пла­чен­ная Алек­се­ем банку за весь срок кре­ди­то­ва­ния, ока­за­лась на 27 % боль­ше, чем сумма, взя­тая им в кре­дит. Най­ди­те r.

12. Баба Валя, на­ко­пив часть своей пен­сии, ре­ши­ла улуч­шить свое ма­те­ри­аль­ное по­ло­же­ние. Она узна­ла, что в Сбер­бан­ке от пен­си­о­не­ров при­ни­ма­ют вкла­ды под опре­де­лен­ный про­цент го­до­вых и на этих усло­ви­ях внес­ла свои сбе­ре­же­ния в бли­жай­шее от­де­ле­ние Сбер­бан­ка. Но через не­ко­то­рое время со­сед­ка ей рас­ска­за­ла, что не­да­ле­ко от той мест­но­сти, где про­жи­ва­ют пен­си­о­не­ры, есть ком­мер­че­ский банк, в ко­то­ром про­цент го­до­вых для пен­си­о­не­ров-вклад­чи­ков в 20 раз выше, чем в Сбер­бан­ке. Баба Валя не до­ве­ря­ла ком­мер­че­ским бан­кам, но стрем­ле­ние улуч­шить свое ма­те­ри­аль­ное по­ло­же­ние взяло верх. После дол­гих ко­ле­ба­ний и ровно через год после от­кры­тия счета в Сбер­бан­ке Баба Валя сняла по­ло­ви­ну об­ра­зо­вав­шей суммы от ее вкла­да, за­явив: «Такой навар меня не устра­и­ва­ет!» И от­кры­ла счет в том ком­мер­че­ском банке, о ко­то­ром го­во­ри­ла ее со­сед­ка, не теряя на­деж­ды на зна­чи­тель­ное улуч­ше­ние сво­е­го ма­те­ри­аль­но­го бла­го­со­сто­я­ния.

На­деж­ды оправ­да­лись: через год сумма Бабы Вали в ком­мер­че­ском банке пре­вы­си­ла ее пер­во­на­чаль­ные кров­ные сбе­ре­же­ния на 65%. Со­жа­ле­ла Баба Валя, что год назад в Сбер­бан­ке сняла не всю сумму, а лишь по­ло­ви­ну, од­на­ко, по­ду­ма­ла: «А где же мы не те­ря­ли?..»

Ген­ди­рек­тор ком­мер­че­ско­го банка ока­зал­ся хо­ро­шим: не оста­вил Бабу Валю без на­ва­ра!

А каков в Сбер­бан­ке про­цент го­до­вых для пен­си­о­не­ров?

13. Банк под опре­де­лен­ный про­цент при­нял не­ко­то­рую сумму. Через год чет­верть на­коп­лен­ной суммы была снята со счета. Банк уве­ли­чил про­цент го­до­вых на 40 про­цент­ных пунк­тов (то есть уве­ли­чил став­ку а% до (а + 40)%). К концу сле­ду­ю­ще­го года на­коп­лен­ная сумма в 1,44 раза пре­вы­си­ла пер­во­на­чаль­ный вклад. Каков про­цент новых го­до­вых?

14. 15-го ян­ва­ря пла­ни­ру­ет­ся взять кре­дит в банке на 39 ме­ся­цев. Усло­вия его воз­вра­та та­ко­вы:

— 1-го числа каж­до­го ме­ся­ца долг воз­растёт на r% по срав­не­нию с кон­цом преды­ду­ще­го ме­ся­ца;

— со 2-го по 14-е число каж­до­го ме­ся­ца не­об­хо­ди­мо вы­пла­тить часть долга;

— 15-го числа каж­до­го ме­ся­ца долг дол­жен быть на одну и ту же сумму мень­ше долга на 15-е число преды­ду­ще­го ме­ся­ца. Из­вест­но, что общая сумма вы­плат после пол­но­го по­га­ше­ния кре­ди­та на 20% боль­ше суммы, взя­той в кре­дит. Най­ди­те r.

15.В 1-е клас­сы по­сту­па­ет 45 че­ло­век: 20 маль­чи­ков и 25 де­во­чек. Их рас­пре­де­ли­ли по двум клас­сам: в одном долж­но по­лу­чить­ся 22 че­ло­ве­ка, а в дру­гом - 23. После рас­пре­де­ле­ния по­счи­та­ли про­цент де­во­чек в каж­дом клас­се и по­лу­чен­ные числа сло­жи­ли. Каким долж­но быть рас­пре­де­ле­ние по клас­сам, чтобы по­лу­чен­ная сумма была наи­боль­шей?

16. Антон яв­ля­ет­ся вла­дель­цем двух за­во­дов в ра­зных го­ро­дах. На за­во­дах про­из­во­дит­ся аб­со­лют­но оди­на­ко­вые то­ва­ры при ис­поль­зо­ва­нии оди­на­ко­вых тех­но­ло­гий. Если ра­бо­чие на одном из за­во­дов тру­дят­ся сум­мар­но t² часов в не­де­лю, то за эту не­де­лю они про­из­водят t еди­ниц то­ва­ра.

За каж­дый час ра­бо­ты на за­во­де, рас­по­ло­жен­ном в пер­вом го­ро­де, Антон пла­тит ра­бо­че­му 250 руб­лей, а на за­во­де, рас­по­ло­жен­ном во вто­ром го­ро­де, — 200 руб­лей.

Антон готов вы­де­лять 900 000 руб­лей в не­де­лю на опла­ту труда ра­бо­чих. Какое наи­боль­шее ко­ли­че­ство еди­ниц то­ва­ра можно про­из­ве­сти за не­де­лю на этих двух за­во­дах?

17. В 1-е клас­сы по­сту­па­ет 43 че­ло­ве­ка: 23 маль­чи­ка и 20 де­во­чек. Их рас­пре­де­ли­ли по двум клас­сам: в одном долж­но по­лу­чить­ся 22 че­ло­ве­ка, а в дру­гом ? 21. После рас­пре­де­ле­ния по­счи­та­ли про­цент маль­чи­ков в каж­дом клас­се и по­лу­чен­ные числа сло­жи­ли. Каким долж­но быть рас­пре­де­ле­ние по клас­сам, чтобы по­лу­чен­ная сумма была наи­боль­шей?

18. 31 де­каб­ря 2013 года Сер­гей взял в банке 9 930 000 руб­лей в кре­дит под 10% го­до­вых. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая: 31 де­каб­ря каж­до­го сле­ду­ю­ще­го года банк на­чис­ля­ет про­цен­ты на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 10%), затем Сер­гей пе­ре­во­дит в банк опре­делённую сумму еже­год­но­го пла­те­жа. Какой долж­на быть сумма еже­год­но­го пла­те­жа, чтобы Сер­гей вы­пла­тил долг тремя рав­ны­ми еже­год­ны­ми пла­те­жа­ми?

19. 1 ян­ва­ря 2015 года Павел Ви­та­лье­вич взял в банке 1 млн руб­лей в кре­дит. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая: 1 числа каж­до­го сле­ду­ю­ще­го ме­ся­ца банк на­чис­ля­ет 1 про­цент на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 1%), затем Павел Ви­та­лье­вич пе­ре­во­дит в банк платёж. НА какое ми­ни­маль­ное ко­ли­че­ство ме­ся­цев Павел Ви­та­лье­вич может взять кре­дит, чтобы еже­ме­сяч­ные вы­пла­ты были не более 125 тыс. руб­лей?

20. Кон­серв­ный завод вы­пус­ка­ет фрук­то­вые ком­по­ты в двух видах тары — стек­лян­ной и же­стя­ной. Про­из­вод­ствен­ные мощ­но­сти за­во­да поз­во­ля­ют вы­пус­кать в день 90 цент­не­ров ком­по­тов в стек­лян­ной таре или 80 цент­не­ров в же­стя­ной таре. Для вы­пол­не­ния усло­вий ас­сор­ти­мент­но­сти, ко­то­рые предъ­яв­ля­ют­ся тор­го­вы­ми се­тя­ми, про­дук­ции в каж­дом из видов тары долж­но быть вы­пу­ще­но не менее 20 цент­не­ров. В таб­ли­це при­ве­де­ны се­бе­сто­и­мость и от­пуск­ная цена за­во­да за 1 цент­нер про­дук­ции для обоих видов тары.

Вид тары	Се­бе­сто­и­мость, 1 ц.	От­пуск­ная цена, 1 ц.
стек­лян­ная	1500 руб.	2100 руб.
же­стя­ная	1100 руб.	1750 руб.

Пред­по­ла­гая, что вся про­дук­ция за­во­да на­хо­дит спрос (ре­а­ли­зу­ет­ся без остат­ка), най­ди­те мак­си­маль­но воз­мож­ную при­быль за­во­да за один день (при­бы­лью на­зы­ва­ет­ся раз­ни­ца между от­пуск­ной сто­и­мо­стью всей про­дук­ции и её се­бе­сто­и­мо­стью).

21.31 де­каб­ря 2014 года Яро­слав взял в банке не­ко­то­рую сумму в кре­дит под 12,5% го­до­вых. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая: 31 де­каб­ря каж­до­го сле­ду­ю­ще­го года банк на­чис­ля­ет про­цен­ты на остав­шу­ю­ся сумму долга ( то есть уве­ли­чи­ва­ет долг на 12,5%), затем Яро­слав пе­ре­во­дит в банк 2 132 325 руб­лей. Какую сумму взял Яро­слав в банке, если он вы­пла­тил долг че­тырь­мя рав­ны­ми пла­те­жа­ми (то есть за че­ты­ре года)?

22. Два бро­ке­ра ку­пи­ли акции од­но­го до­сто­ин­ства на сумму 3640 р. Когда цена на эти акции воз­рос­ла, они про­да­ли часть акций на сумму 3927 р. Пер­вый бро­кер про­дал 75% своих акций, а вто­рой 80% своих. При этом сумма от про­да­жи акций, по­лу­чен­ная вто­рым бро­ке­ром, на 140% пре­вы­си­ла сумму, по­лу­чен­ную пер­вым бро­ке­ром. На сколь­ко про­цен­тов воз­рос­ла цена одной акции?

23. Оля хочет взять в кре­дит 1 200 000 руб­лей. По­га­ше­ние кре­ди­та про­ис­хо­дит раз в год рав­ны­ми сум­ма­ми (кроме, может быть, по­след­ней) после на­чис­ле­ния про­цен­тов. Став­ка про­цен­та 10 % го­до­вых. На какое ми­ни­маль­ное ко­ли­че­ство лет может Оля взять кре­дит, чтобы еже­год­ные вы­пла­ты были не более 320 000 руб­лей?

24. 31 де­каб­ря 2013 года Сер­гей взял в банке 9 930 000 руб­лей в кре­дит под 10% го­до­вых. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая: 31 де­каб­ря каж­до­го сле­ду­ю­ще­го года банк на­чис­ля­ет про­цен­ты на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 10%), затем Сер­гей пе­ре­во­дит в банк опре­делённую сумму еже­год­но­го пла­те­жа. Какой долж­на быть сумма еже­год­но­го пла­те­жа, чтобы Сер­гей вы­пла­тил долг тремя рав­ны­ми еже­год­ны­ми пла­те­жа­ми?

25. Сер­гей взял кре­дит в банке на срок 9 ме­ся­цев. В конце каж­до­го ме­ся­ца общая сумма остав­ше­го­ся долга уве­ли­чи­ва­ет­ся на 12%, а затем умень­ша­ет­ся на сумму, упла­чен­ную Сер­ге­ем. Суммы, вы­пла­чи­ва­е­мые в конце каж­до­го ме­ся­ца, под­би­ра­ют­ся так, чтобы в ре­зуль­та­те сумма долга каж­дый месяц умень­ша­лась рав­но­мер­но, то есть на одну и ту же ве­ли­чи­ну.

Сколь­ко про­цен­тов от суммы кре­ди­та со­ста­ви­ла общая сумма, упла­чен­ная Сер­ге­ем банку (сверх кре­ди­та)?

26. 31 де­каб­ря 2014 года Алек­сей взял в банке 6 902 000 руб­лей в кре­дит под 12,5% го­до­вых. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая — 31 де­каб­ря каж­до­го сле­ду­ю­ще­го года банк на­чис­ля­ет про­цен­ты на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 12,5%), затем Алек­сей пе­ре­во­дит в банк X руб­лей. Какой долж­на быть сумма X, чтобы Алек­сей вы­пла­тил долг че­тырь­мя рав­ны­ми пла­те­жа­ми (то есть за че­ты­ре года)?

27.Алек­сей при­обрёл цен­ную бу­ма­гу за 7 тыс. руб­лей. Цена бу­ма­ги каж­дый год воз­рас­та­ет на 2 тыс. руб­лей. В любой мо­мент Алек­сей может про­дать бу­ма­гу и по­ло­жить вы­ру­чен­ные день­ги на бан­ков­ский счёт. Каж­дый год сумма на счёте будет уве­ли­чи­вать­ся на 10 %. В те­че­ние ка­ко­го года после по­куп­ки Алек­сей дол­жен про­дать цен­ную бу­ма­гу, чтобы через трид­цать лет после по­куп­ки этой бу­ма­ги сумма на бан­ков­ском счёте была наи­боль­шей?

28. Оля хочет взять в кре­дит 100 000 руб­лей. По­га­ше­ние кре­ди­та про­ис­хо­дит раз в год рав­ны­ми сум­ма­ми (кроме, может быть, по­след­ней) после на­чис­ле­ния про­цен­тов. Став­ка про­цен­та 10 % го­до­вых. На какое ми­ни­маль­ное ко­ли­че­ство лет может Оля взять кре­дит, чтобы еже­год­ные вы­пла­ты были не более 24000 руб­лей?

29. 1 ян­ва­ря 2015 года Алек­сандр Сер­ге­е­вич взял в банке 1,1 млн руб­лей в кре­дит. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая — 1 числа каж­до­го сле­ду­ю­ще­го ме­ся­ца банк на­чис­ля­ет 1 про­цент на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 1%), затем Алек­сандр Сер­ге­е­вич пе­ре­во­дит в банк платёж. На какое ми­ни­маль­ное ко­ли­че­ство ме­ся­цев Алек­сандр Сер­ге­е­вич может взять кре­дит, чтобы еже­ме­сяч­ные вы­пла­ты были не более 275 тыс. руб­лей?

30. 31 де­каб­ря 2014 года Пётр взял в банке не­ко­то­рую сумму в кре­дит под не­ко­то­рый про­цент го­до­вых. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая — 31 де­каб­ря каж­до­го сле­ду­ю­ще­го года банк на­чис­ля­ет про­цен­ты на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на а%), затем Пётр пе­ре­во­дит оче­ред­ной транш. Если он будет пла­тить каж­дый год по 2 592 000 руб­лей, то вы­пла­тит долг за 4 года. Если по 4 392 000 руб­лей, то за 2 года. Под какой про­цент Пётр взял день­ги в банке?

Немного теории

Сначала рассмотрим так называемые «банковские» задачи: варианты, когда имеет дело с вкладом и кредиты.

Рассмотрим вариант, когда мы вкладываем деньги в банк на N лет некоторую сумму S под r% годовых.

1. Через год имеем на счету S₁= S+r/100* S=(1+r/100) S

2. Через два года на счету будет S₂=(1+r/100)* S +((1+r/100)*S)*r/100=((1+r/100)*S)(1+r/100)=(1+r/100)²*S

3. Продолжая аналогичную схему рассуждения получим:

S_n=(1+r/100)ⁿ*S - (1)

Для более компактной записи формулы (1) введем замену переменной q=(1+r/100)и формула (1) примет вид: S_n =qⁿ *S (2)

Рассмотрим вариант, когда мы берем кредит в банке на N лет некоторую сумму S под r% годовых.

1. К концу 1 года, наш долг увеличился на заявленные банком проценты, а мы платим заявленный платеж. Пусть Х- ежегодный платеж. Долг наш будет иметь следующий вид: 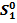=S+r*S-X=(1+r)*S-X=q*S-X

2. Через год долг будет: 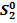= (q*S-X)+(q*S-X)*r-X=(q*S-X)(1+r)-X= (q*S-X)*q-X=q²*S-q*X-X=q²*S-(1+q)X

3. Аналогично продолжая рассуждения получим, что к концу договора мы полностью выплачиваем кредит и 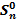=qⁿ*S-(1+q)^n-1*X.Так как кредит выплачен полностью, то

qⁿ*S-(1+q+q²+….+q^n-1)*X =qⁿ*S-(1+q)^n-1*X=0.Следовательно, qⁿ*S=(1+q)^n-1*X. qⁿ*S-(1+q)^n-1*X.Домножив и разделив правую часть на (q-1)получим:

qⁿ*S= 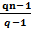*X (3)

Для облегчения решения задач предлагаю воспользоваться следующими формулами, которые можете доказать самостоятельно:

1. Если величину х увеличить на р % , то получим х·(1+р/100)

2. Если величину х уменьшить на р % , то получим х·(1-р/100)

3. Если величину х увеличить на р %, а затем уменьшить на q %, то получим х·(1+р/100)(1-q/100)

4. Если величину х увеличить дважды на р%, получим х·(1+р/100)²

5. Если величину х уменьшить дважды на р%, получим х·(1-р/100)²

тип. Определение суммы кредита

Задача 1.1

31 декабря 2014 года Василий взял в банке некоторую сумму в кредит под 11% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 11%), затем Василий переводит в банк 3696300 рублей. Какую сумму Василий взял в кредит в банке, если он выплатил долг двумя платежами (т.е. за 2 года)?

Решение:

1 способ:

Пусть S- сумма кредита, Х- выплачиваемая сумма, r- процентная ставка и Х=3696300 рублей, r=11% или r=0,11, n=2.

Тогда q²*S=(q²-1)/(q-1)*X. Следовательно, S=((q+1)*X)/q². Получим, что Василий взял в кредит 6330000 рублей. Ответ:6330000

2 способ:

1. К концу первого года мы имеем долг: 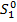=S+0.11*S –Х=1.11*S-X

2.Через год остаток после выплаты будет: 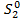=(1.11*S-X)+(1.11*S-X)*0.11-X=(1.11*S-X)*1.11-X=1.11²*S-2.11*X. Так как Василий выплатил долг за два транша, то 1.11²*S-2.11*X=0. Решив полученное уравнение, имеем: S=2.11*3696300/1,2321=6330000 рублей.

Ответ: 6330000

Задача № 1.2

15 января планируется взять в кредит в банке на 15 месяцев. Условия его возврата таковы:

– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;

– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.