Теорема Пуассона. Простейший поток событий
Если число n испытаний достаточно велико, а вероятность p наступления события А в независимых испытаниях мала, то для нахождения вероятности 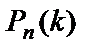 используется теорема Пуассона: Если в n независимых испытаниях вероятность p наступления события А в каждом из них постоянна и мала, а число испытаний достаточно велико, то вероятность того, что событие А наступит k раз, вычисляется по формуле
используется теорема Пуассона: Если в n независимых испытаниях вероятность p наступления события А в каждом из них постоянна и мала, а число испытаний достаточно велико, то вероятность того, что событие А наступит k раз, вычисляется по формуле 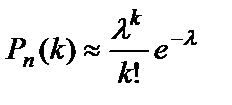 , где
, где 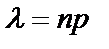 .
.
Эта формула называется формулой Пуассона.
Пример 15. Вероятность попадания в самолёт при каждом выстреле из пулемёта равна 0.001. Производится 3000 выстрелов. Найти вероятность попадания в самолёт: а) один или два раза; б) хотя бы один раз.
Решение. По условию примера n=300, p=0.001, 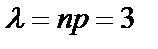 .
.
а) Обозначим событие A={попадание в самолёт один или два раза}. Тогда 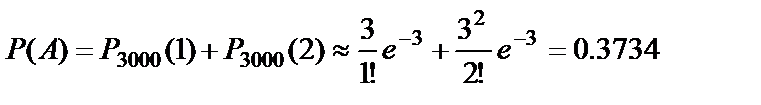 .
.
б) Обозначим событие B={попадание в самолёт хотя бы один раз}. Тогда 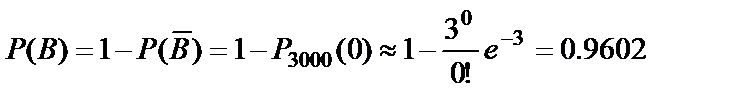 .
.
Потоком событий называется последовательность событий, которые наступают одно за другим в случайные моменты времени.
Например, поток вызовов в сфере обслуживания (ремонт телевизоров, вызовы скорой помощи и др.), поток вызовов на телефонной станции, отказ в работе отдельных частей некоторой системы и т.д.
Поток называется простейшим, если выполняются следующие условия:
 вероятность появления события зависит от длины промежутка времени t;
вероятность появления события зависит от длины промежутка времени t;
 вероятность появления числа событий на любом промежутке времени не зависит от того, какое число событий наступило до начала этого промежутка;
вероятность появления числа событий на любом промежутке времени не зависит от того, какое число событий наступило до начала этого промежутка;
 вероятность наступления двух или большего числа событий за достаточно малый промежуток времени
вероятность наступления двух или большего числа событий за достаточно малый промежуток времени 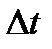 мала и чем меньше
мала и чем меньше 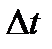 , тем меньше становится вероятность.
, тем меньше становится вероятность.
При выполнении этих условий справедливо следующее утверждение:
Вероятность того, что случайное событие за время t наступит k раз, определяется по формуле
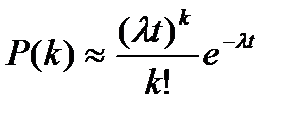 ,
,
где 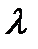 - среднее число событий, наступающих в единицу времени.
- среднее число событий, наступающих в единицу времени.
Пример 16. На ткацких станках, обслуживаемых ткачихой, в течение часа происходит 90 обрывов нити. Какова вероятность того, что за 4 минуты произойдёт: 1) один обрыв; 2) хотя бы один обрыв.
Решение. По условию t=4. Среднее число обрывов за одну минуту равно 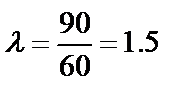 . Тогда
. Тогда 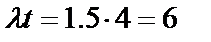 .
.
1) 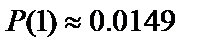 . 2)
. 2) 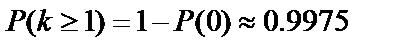 .
.
Вопросы для самоконтроля знаний
1. Что называется суммой совместных событий?
2. Что называется суммой несовместных событий?
3. Как формулируется теорема сложения вероятностей несовместных событий?
4. Чему равна сумма вероятностей противоположных событий?
5. Что называется произведением двух событий?
6. Какие события называются независимыми?
7. Как формулируется теорема умножения вероятностей независимых событий?
8. Какие события называются зависимыми?
9. Что называется условной вероятностью?
10. Как формулируется теорема умножения вероятностей зависимых событий?
11. Что называется полной вероятностью события и как записывается формула полной вероятности?
12. Как записывается формула Байеса?
13. Какие испытания называются независимыми и как записывается формула Бернулли?
14. Как формулируется локальная теорема Лапласа?
15. Как формулируется интегральная теорема Лапласа?
16. Как формулируется теорема Пуассона?
