Классификация бактерий по отношению к температуре
| Наименование группы бактерий | Подгруппа | Температурный интервал роста (от … до …), °С | Диапазон оптимальных температур, °С |
| Психрофилы | Облигатные психрофилы | от –(10¸20) до +20 | 5¸15 |
| Факультативные психрофилы | от –10 до +(32¸35) | 20¸30 | |
| Мезофилы | - | от +10 до +(42¸45) | 30¸40 |
| Факультативные термофилы | от +20 до +(70¸80) | 60¸70 | |
| Термофилы | Облигатные термофилы | от +(42¸42) до +(65¸70) | 50¸60 |
Для описания влияния температуры на скорость роста микроорганизмов применяют следующие уравнения:
· уравнение Аррениуса
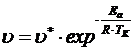 ; (5.1)
; (5.1)
· эмпирическая формула СНиП 2.04.03-85
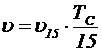 ; (5.2)
; (5.2)
· эмпирическая зависимость
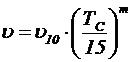 , (5.3)
, (5.3)
| где | 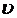 – скорость роста (или скорость потребления кислорода), мг/(л×ч); – скорость роста (или скорость потребления кислорода), мг/(л×ч); |
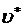 – константа, мг/(л×ч); – константа, мг/(л×ч); | |
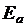 – энергия активации, ккал/моль; – энергия активации, ккал/моль; | |
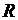 – универсальная газовая постоянная, R=1,98×10-3 ккал/(моль×K); – универсальная газовая постоянная, R=1,98×10-3 ккал/(моль×K); | |
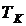 – абсолютная температура, °K; – абсолютная температура, °K; | |
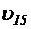 , , 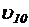 – скорость роста (или скорость потребления кислорода) при температуре 15 и 10°С соответственно, мг/(л×ч); – скорость роста (или скорость потребления кислорода) при температуре 15 и 10°С соответственно, мг/(л×ч); | |
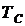 – температура, °С; – температура, °С; | |
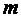 – эмпирический коэффициент. – эмпирический коэффициент. |
С целью интерполяции, экстраполяции, а также выявления механизма изучаемого процесса, часто возникает задача выбора уравнения регрессии, которое наиболее полно описывает экспериментальные данные. В основе такого выбора лежит минимум относительной ошибки расчета по уравнению регрессии в сравнении с экспериментальными значениями.
Включаемые в рассмотрение уравнения регрессии выводятся теоретически, исходя из гипотез о механизме исследуемого процесса, или используются эмпирические уравнения.
Уравнение (5.2) является линейным уравнением вида 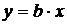 , где
, где 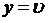 ;
; 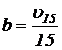 ;
; 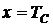 . Если мы имеем экспериментальные данные значений скорости
. Если мы имеем экспериментальные данные значений скорости 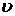 при различных температурах
при различных температурах 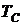 , то методом наименьших квадратов можем найти параметры линейной регрессии и величину стандартного отклонения:
, то методом наименьших квадратов можем найти параметры линейной регрессии и величину стандартного отклонения:
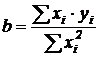 ;
; 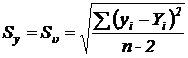 , (5.4)
, (5.4)
где 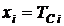 ;
; 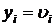 ;
; 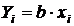 ;
; 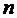 – объем выборки (число измерений). Тогда абсолютная ошибка расчета по уравнению (5.2) составит:
– объем выборки (число измерений). Тогда абсолютная ошибка расчета по уравнению (5.2) составит:
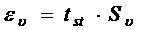 ,
,
где 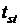 – стандартный критерий Стьюдента.
– стандартный критерий Стьюдента.
Если обозначить: 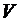 – значения
– значения 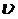 на линии регрессии, то получим относительную ошибку
на линии регрессии, то получим относительную ошибку 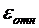 :
:
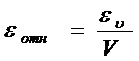 . (5.5)
. (5.5)
Как видно, 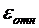 не является постоянной: с увеличением величины
не является постоянной: с увеличением величины 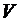 происходит уменьшение
происходит уменьшение 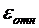 . Если экспериментальный диапазон значений
. Если экспериментальный диапазон значений 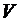 составляет (
составляет ( 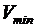 ,
, 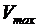 ), то средняя относительная ошибка уравнения (5.2) в этом диапазоне:
), то средняя относительная ошибка уравнения (5.2) в этом диапазоне:
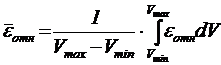 . (5.6)
. (5.6)
После подстановки формулы для 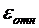 (5.5) в уравнение (5.6), получим:
(5.5) в уравнение (5.6), получим:
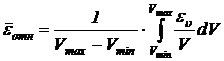 . (5.7)
. (5.7)
Интегрирование выражения (5.7) позволяет получить расчетную формулу для вычисления 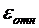 уравнения (5.2):
уравнения (5.2):
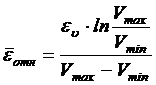 .
.
Для применения метода наименьших квадратов к уравнениям (5.1) и (5.3) необходима их линеаризация, которая достигается путем логарифмирования:
· для уравнения (5.1):
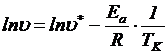 (5.8)
(5.8)
или 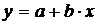 ,
,
где 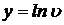 ;
; 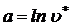 ;
; 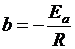 ;
; 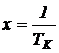 .
.
· для уравнения (5.3):
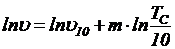 (5.9)
(5.9)
или 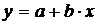 ,
,
где 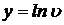 ;
; 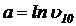 ;
; 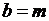 ;
; 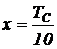 .
.
По методу наименьших квадратов параметры линеаризованных уравнений (5.8), (5.9), стандартные отклонения и абсолютные ошибки составят:
· для уравнения (5.8):
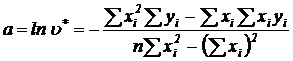 ; (5.10)
; (5.10)
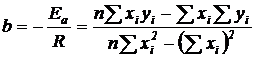 ; (5.11)
; (5.11)
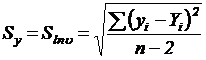 ;
; 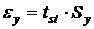 , (5.12)
, (5.12)
где 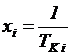 ;
; 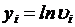 ;
; 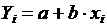 ;
; 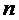 – объем выборки (число экспериментальных точек);
– объем выборки (число экспериментальных точек); 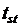 – стандартный критерий Стьюдента при доверительной вероятности 95 % и степеней свободы
– стандартный критерий Стьюдента при доверительной вероятности 95 % и степеней свободы 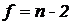 .
.
· для уравнения (5.9):
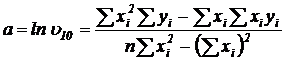 ; (5.13)
; (5.13)
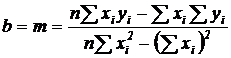 ; (5.14)
; (5.14)
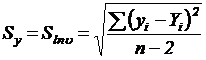 ;
; 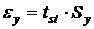 , (5.15)
, (5.15)
где 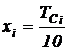 ;
; 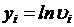 ;
; 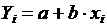 .
.
Так как с доверительной вероятностью 95 % величина 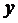 находится в интервале:
находится в интервале:
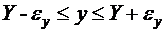 ;
; 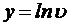 ;
; 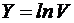 ,
,
то абсолютная ошибка уравнений (5.1) и (5.3) будет равна:
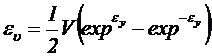 , (5.16)
, (5.16)
где 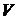 – значение
– значение 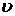 на линии регрессии.
на линии регрессии.
Относительная ошибка уравнений (5.1) и (5.3) может быть найдена, если подставить выражение (5.16) в формулу (5.5):
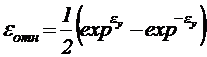 ,
,
где 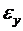 – по уравнениям (5.12) и (5.15).
– по уравнениям (5.12) и (5.15).
Параметры уравнений (5.1), (5.2) и (5.3) задаются соотношениями:
· для уравнения (5.1):
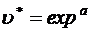 ;
; 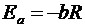 ,
,
где 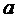 – по уравнению (5.10),
– по уравнению (5.10), 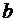 – по уравнению (5.11);
– по уравнению (5.11);
· для уравнения (5.2):
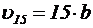 ,
,
где 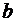 – по уравнению (5.4);
– по уравнению (5.4);
· для уравнения (5.3):
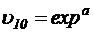 ;
; 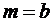 ,
,
где 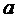 – по уравнению (5.13),
– по уравнению (5.13), 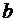 – по уравнению (5.14).
– по уравнению (5.14).
Задание.
1. Экспериментально получить зависимость скорости потребления кислорода активным илом от температуры в процессе роста на сложном субстрате.
2. Выполнить расчет средних относительных ошибок уравнений (5.1), (5.2), (5.3) и выбрать уравнение, наиболее точно описывающее экспериментальные данные. Определить параметры выбранного уравнения.
Ход работы.
| 1. | Из лабораторного аэротенка отобрать в цилиндр 1 л иловой смеси. После 10 минут отстаивания осевший активный ил (около 200 мл) перенести в колбу и при интенсивном перемешивании разделить на 5 равных частей (по 40 мл), каждую из которых поместить в колбы объемом 100 мл. В первой колбе постепенно довести температуру активного ила до 10°С, во второй – до 15°С, в третьей – до 20°С, в четвертой – до 25°С, в пятой – до 30°С. В процессе охлаждения (нагрева) активный ил необходимо периодически аэрировать (или перемешивать). |
| 2. | Приготовить питательную среду (0,5 л) путем разбавления в 100 раз отработанного сульфитного щелока с последующей его нейтрализацией (до рН=7¸8) и добавкой биогенных элементов из расчета БПК5:N:Р=100:5:1 (принять для полученной среды БПК5=200 мг/л). Полученный раствор насытить кислородом (аэрация 10 минут от микрокомпрессора), а затем разделить на 5 частей (по 100 мл) и довести температуру, соответственно, до 10; 15; 20; 25 и 30°С. |
| 3. | Для измерения скорости потребления кислорода активным илом при различных температурах используется оксиметрическая установка (см. рис. 4.3). В окиметрическую ячейку последовательно вводится 30 мл активного ила и 70 мл питательной среды с той же температурой. В ячейку помещают датчик оксиметра, включают перемешивание и снимают динамику уменьшения концентрации кислорода. Скорость потребления кислорода рассчитывают графоаналитически по динамике уменьшения концентрации растворенного кислорода (строят график зависимости 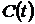 и находят величину максимальной скорости потребления кислорода). Группа студентов (около 10 человек) делится на 5 бригад (по 2 человека). Каждая бригада определяет скорость потребления кислорода при одной заданной температуре. Полученная зависимость скорости от температуры изображается в виде графика и находят величину максимальной скорости потребления кислорода). Группа студентов (около 10 человек) делится на 5 бригад (по 2 человека). Каждая бригада определяет скорость потребления кислорода при одной заданной температуре. Полученная зависимость скорости от температуры изображается в виде графика 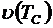 . Если во всем температурном диапазоне скорость возрастает, то в дальнейших расчетах учитываются все пять экспериментальных точек. В противном случае отбор данных для дальнейших расчетов выполняется совместно с преподавателем. . Если во всем температурном диапазоне скорость возрастает, то в дальнейших расчетах учитываются все пять экспериментальных точек. В противном случае отбор данных для дальнейших расчетов выполняется совместно с преподавателем. |
| 4. | Полученные результаты обрабатываются, как описано выше. Выбирается уравнение (см. уравнения 5.1-5.3), дающее наименьшую относительную ошибку 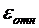 . Для выбранного уравнения находятся входящие в него параметры. Выбранное уравнение приводится в окончательном виде (после подстановки значений параметров) с указанием абсолютной ошибки. . Для выбранного уравнения находятся входящие в него параметры. Выбранное уравнение приводится в окончательном виде (после подстановки значений параметров) с указанием абсолютной ошибки. |
Лабораторная работа № 6
