ЛЕКЦИЯ 6. Электромагнитные колебания. Электромагнитные волны. Переменный ток
Свободные электромагнитные колебания.
В физике колебанияминазывают процессы, отличающиеся той или иной степенью повторяемости.
Электромагнитные колебания- это повторяющиеся изменения электрических и магнитных величин: заряда, тока, напряжения, а также электрического и магнитного полей.
Такие колебания возникают, например, в замкнутой цепи, содержащей конденсатор и катушку индуктивности (колебательный контур).
Незатухающие колебания
Рассмотрим идеальный колебательный контур, который не обладает активным сопротивлением (рис. 9.1).
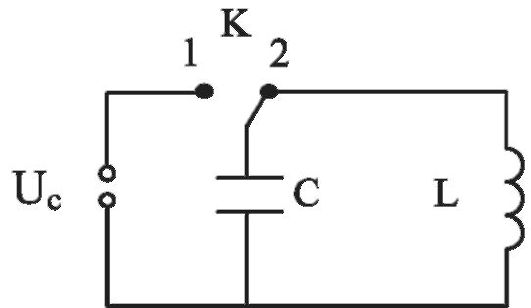
Рис. 9.1.Идеальный колебательный контур (С - емкость конденсатора, L - индуктивность катушки) появится нарастающий ток i (силу переменного тока обозначают строчнойбуквой i).
Если зарядить конденсатор от сети постоянного напряжения (Uc), установив ключ К в положение «1», а затем перевести ключ К в положение «2», то конденсатор начнет разряжаться через катушку индуктивности.
При этом в катушке возникает э.д.с. самоиндукции Е = - L*di/dt . В идеальном контуре (R = 0), э.д.с. равна напряжению U на обкладках конденсатора, которое можно определит по формуле U = q/C.
Изменение заряда конденсатора в процессе свободных колебаний в идеальном контуре определяют по формуле:
q = qmax∙cos(ωоt)
Период свободных колебаний в идеальном контуре:
T = 2π/ωо=2π 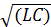
где 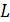 - индуктивность, С – емкость.
- индуктивность, С – емкость.
Приравняв Е и U, получим формулу полной энергии электромагнитных колебаний в идеальном контуре:
W = C U2max/2 = L I2max/2
где 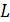 - индуктивность, С – емкость, I - ток, U - напряжение цепи.
- индуктивность, С – емкость, I - ток, U - напряжение цепи.
Условия возникновения затухающих колебаний в реальном контуре –
R =2π 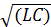 - (слабое затухание)
- (слабое затухание)
Циклическая частота затухающих колебаний:
- ω3= 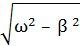 , где ω2 =
, где ω2 =
Изменение заряда конденсатора в реальном контуре в процессе затухающих колебаний:
q = qmax∙cos(ωоt) ехр(-βt)
Логарифмический декремент затухания (расчетная формула):
λ= βT3 = 2π β/ω3
Апериодический разряд конденсатора через резистор:
- q = qmax∙ ехр(-t/τ),
где τ – RС – постоянная времени.
Затухающие колебания
В обычных условиях все проводники обладают активным сопротивлением.Поэтому свободные колебания в реальном контуре затухают. На рисунке 9.2 активное сопротивление проводников изображает резистор R.
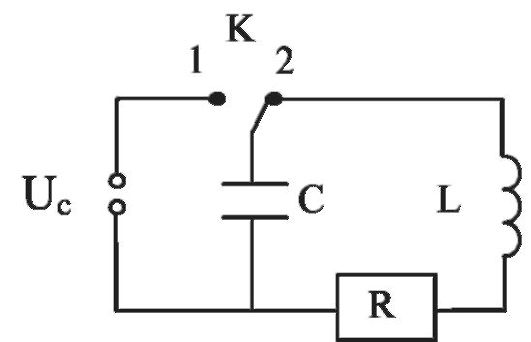
Рис. 9.2. Реальный колебательный контур
При наличии активного сопротивления э.д.с. самоиндукции равна сумме напряжений на резисторе и обкладках конденсатора:
- 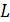 di/dt = iR + q/C
di/dt = iR + q/C
Сила тока равна произведению заряда по времени: i = dq /dt. Поэтому
- 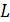 d2q/dt2 = R dq/dt + q/C
d2q/dt2 = R dq/dt + q/C
После переноса всех слагаемых в левую часть и деления на индуктивность катушки (L) получим дифференциальное уравнение свободных колебаний в реальном контуре:
d2q/dt2 + 2βdq/dt + ωо2 q = 0 (1)
Коэффициент затухания колебаний β в реальном контуре: β = R/2L
Циклическая частота свободных колебаний в идеальном контуре определяют по формуле: ωо = 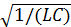
Условия возникновения затухающих колебаний в реальном контуре при выполнении равенства R = 2π 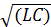 – будет слабое затухание.
– будет слабое затухание.
При выполнении условия R 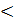 2
2 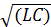 , уравнение 1 описывает затухающие колебания: q = qmax∙cos(ω3t) ехр(- βt), и циклическая частота ω3 меньше частоты незатухающих колебаний, а амплитуда убывает по экспоненциальному закону: ω3=
, уравнение 1 описывает затухающие колебания: q = qmax∙cos(ω3t) ехр(- βt), и циклическая частота ω3 меньше частоты незатухающих колебаний, а амплитуда убывает по экспоненциальному закону: ω3= 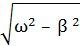 ; А = qmax∙ ехр(- βt),
; А = qmax∙ ехр(- βt),
График таких колебаний представлен на рис. 9.3.
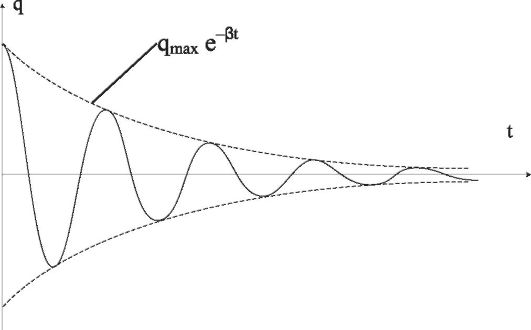
Рис. 9.3. Зависимость заряда от времени в реальном колебательном контуре (затухающие колебания)
Характеристикой затухания является логарифмический декремент затуханияλ = βТз = 2πβ/ωз, где Тз и ωз- период и частота затухающих колебаний соответственно.
При условии R 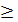 2
2 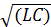 колебаний не возникают и конденсатор просто разряжается. Такой разряд называют апериодическим.
колебаний не возникают и конденсатор просто разряжается. Такой разряд называют апериодическим.
Апериодический разряд конденсатора через резистор:
- q = qmax∙ ехр(-t/τ),
где τ – RС – постоянная времени.
Апериодический разряд конденсатора. Постоянная времени. Зарядка конденсатора
Апериодические процессы возникают и в более простых случаях. Если, например, заряженный конденсатор соединить с резистором (рис. 9.4) или незаряженный конденсатор подключить к источнику постоянного напряжения (рис. 9.5), то после замыкания ключей колебаний не возникнет.
Разрядка конденсатора с начальным зарядом между qmax пластинами происходит по экспоненциальному закону:
q = qmax∙ ехр(-t/τ),
где τ = RC называется постоянной времени.
По такому же закону изменяется и напряжение на обкладках конденсатора:
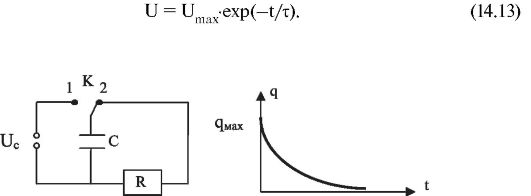
Рис. 9.4.Разряд конденсатора через резистор
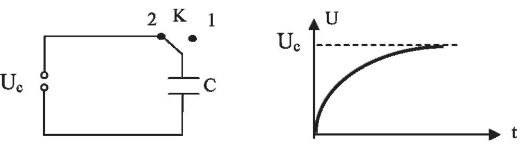
Рис. 9.5.Зарядка конденсатора от сети постоянного тока с внутренним сопротивлением r
При зарядке от сети постоянного тока напряжение на обкладках конденсатора нарастает по закону: U = Uс [1- ехр(-t/τ) ]
где τ = rC также называется постоянной времени(r - внутреннее сопротивление сети).
