Основы теории неньютоновских жидкостей

Реологическая нелинейность (кривая течения или вязкости не является прямой линией) может возникнуть не только в результате комбинации линейных реологических элементов. Отклонения от линейного закона могут возникнуть даже в пределах одного фундаментального реологического свойства. Так, если речь идет о текучих средах, существует целый класс жид­костей, для которых неприменим закон Ньютона, в том числе и в случае, когда нелинейность реологической кривой обусловлена только переменной вязкостью. Жидкости, принадлежащие к этому классу, называются неньютоновскими. Для неньютоновских жидкостей характерно наличие переменной вязкости, зависящей от скорости деформации. Для этого класса жидкос­тей коэффициент вязкости уже не является фундаментальной характеристикой вещества.

Наиболее полной и вместе с тем удобной для практического исследования является классификация неньютоновских жидкостей, преложенная J. Wilkinson (1964).

Классификация неньютоновских жидкостей [Wilkinson J., 1964, с дополнениями]

1. Жидкости, для которых характерна определенная зависимость между скоростью де­
формации и напряжением в определенном месте потока.

1.1. Пластичные жидкости (вязкопластичные).

1.1.1.Линейно-вязкопластичные жидкости.

1.1.2.Нелинейно-вязкопластичные жидкости.

1.2. Псевдопластичные жидкости.

1.3. Дилансные жидкости.

2. Жидкости, для которых зависимость между скоростью деформации и напряжением
определяется (в том числе) временем действия напряжения и (или) предысторией
жидкости.

2.1. Тиксотропные жидкости.

2.2. Реонектические жидкости.

3. Жидкости, обладающие одновременно свойствами твердого тела и жидкости, частич­
но проявляющие упругое восстановление формы после ликвидации напряжения (вяз-
коупругие жидкости).

Жидкости, принадлежащие к 1-й и 3-й группам, могут быть отнесены к реостабильным жидкостям, т.е. таким, реологические характеристики которых не зависят от продолжитель­ности сдвигового течения. Их называют также жидкостями со стационарной реологией.

Реологические особенности линейно-вязкопластичных жидкостей уже рассматривались на примере тела Шведова. Нелинейно-вязкопластичные среды, имеющие прямое отношение к реологии крови, будут рассмотрены на ее примере.

Упруговязкая жидкость является представителем 3-го типа неньютоновских жидкостей. Основными отличиями упруговязкой жидкости от ньютоновской являются следующие. Если в емкость с упруговязкой жидкостью опустить вращающийся стержень, то она как бы «нама­тывается» на него и поднимается вверх по стержню на определенную высоту (ньютоновская жидкость в такой ситуации просто отбрасывается в стороны под действием центробежных сил). Если такую жидкость поместить между двумя параллельными дисками, в ней возника­ют напряжения, нормальные (перпендикулярные) плоскостям дисков, которые под действи­ем этих напряжений раздвигаются (ньютоновская жидкость в данном случае просто растека­ется). Таким образом, при течении упруговязкой жидкости по трубе создается большее по сравнению с ньютоновской жидкостью давление на стенку. И, наконец, ламинарная струя упруговязкой жидкости после выхода из капиллярной трубки утолщается. Сущность этих так называемых эффектов Вейссенберга состоит в возникновении в такой жидкости, помимо ка­сательных, нормальных (перпендикулярных) напряжений. Физическая сущность возникно­вения нормальных напряжений в упруговязкой жидкости до конца не выяснена.

Из представленных на рис. 10.5 графиков следует, что главной особенностью дилансных и псевдопластичных жидкостей является зависимость вязкости от скорости деформации. Кривые течения этих текучих сред выходят из начала координат. Обычно жидкости с такой кривой течения хорошо описываются степенной функцией. Используя обозначения, приня­тые в реологии, ее можно записать:

x = к- Г ⁽¹⁴⁾

где к — показатель консистенции, п — индекс течения.

Заметим, что при п = 1 степенной закон принимает вид закона Ньютона: т = к • у, где параметр к тождествен коэффициенту вязкости.

При 0<п<1 кривая течения соответствует псевдопластичной жидкости и обращена вы­пуклостью в сторону оси напряжения сдвига (см. рис. 10.5, 6, кривая 2). При перестройке кривой течения в кривую вязкости видно (см. рис. 10.5, а, кривая 2), что у такой жидкости вязкость уменьшается с возрастанием скорости деформации. В настоящее время существуют два классических толкования природы явления псевдопластичности: 1) уменьшение вязкос­ти с ростом скорости деформации является следствием «ориентационного» эффекта; 2) явле­ние переменной вязкости может быть обусловлено наличием сольватных оболочек вокруг отдельных частиц псевдопластичной среды. Оба толкования предполагают наличие у обсуж­даемого класса текучих сред определенной структуры. Под структурой в данном случае под-

разумевается наличие в материалах (среде) агрегатов и флоккул коллоидных и микроскопи­ческих частиц. Таким образом, речь обычно идет о дисперсиях, т. е. текучих системах, состо­ящих по меньшей мере из двух фаз — дисперсной фазы (взвешенные частицы) и дисперси­онной (несущей) фазы. Не останавливаясь подробно на особенностях различных видов дис­персий, охарактеризуем лишь те их параметры, которые наиболее существенны с точки зре­ния реологии. Дисперсии с размерами частиц дисперсной фазы 0,1 мкм и более принято считать грубодисперсными. К ним, в частности, относятся суспензии и эмульсии. Суспен­зия — это дисперсная система, в которой дисперсная фаза является твердым веществом, а дисперсионная среда — жидкостью; эмульсия представляет собой взвесь частиц жидкости в жидкой дисперсионной среде. Различают также коллоидные системы. Они имеют размеры частиц дисперсной фазы от 10~⁹ до 10~" м. Примером коллоидной системы может служить, например, раствор альбумина. Классификация дисперсий предусматривает также молеку-лярно-дисперсные и ионно-дисперсные системы, не имеющие существенного значения для реологических свойств исследуемой среды.

При анализе реологических свойств дисперсных систем важно учитывать, что сущест­венным является лишь ограничение, налагаемое на размеры элементов дисперсной фазы «сверху», которое заключается в том, что они должны быть не больше характерных размеров трубки, по которой течет суспензия. Например, при движении эритроцита размером 10 мкм по сосуду диаметром 20 мкм будут иметь место различные пристеночные эффекты, например проскальзывание. Напротив, в сосуде диаметром 250 мкм этими эффектами уже можно пре­небречь.

Наличие у псевдопластичного материала структуры в виде элементов дисперсной среды или ее возникновение в процессе течения приводит к большей кажущейся вязкости вследст­вие создания агрегатами дополнительного торможения смещению одного слоя среды по от­ношению к другому. Существенно, что кажущаяся вязкость псевдопластичной жидкости яв­ляется функцией объема структуры, а не числа частиц, входящих в ее состав [Фукс Г.И., 1951], т.е. при прочих равных условиях рыхлые структуры вызывают более значительное уве­личение вязкости, чем компактные с тем же абсолютным количеством частиц.

Элементы указанных сред в случае низких или нулевых скоростей деформации движутся беспорядочно вследствие тепловых броуновских движений. При увеличении градиента ско­рости у частиц появляется некоторый вращающий момент силы относительно их оси, стре­мящийся сориентировать эти частицы вдоль направления течения. Таким образом, значи­тельная ньютоновская вязкость обусловлена преобладанием броуновского движения над слабым ориентирующим эффектом течения при малых скоростях деформации. По мере на­растания скорости деформации ориентирующий эффект начинает преобладать. В результате этого процесса наименьшая (ньютоновская) вязкость псевдопластической жидкости при больших скоростях деформации обусловлена максимальной ориентацией частиц и полным подавлением влияния броуновского взаимодействия. Б.М. Смольский и соавт. (1970) указы­вают, что в этих случаях с увеличением скорости деформации вязкость всегда убывает ввиду того, что движение дисперсионной среды относительно хаотично расположенной дисперс­ной фазы сопровождается гораздо большими потерями энергии, чем при прохождении через своего рода «решетку» упорядоченно ориентированных частиц.

Второй механизм возникновения псевдопластичности связан с наличием сольватных оболочек на элементах дисперсной фазы: всякая несущая заряд частица (ион, молекула) в растворе окружена сольватной оболочкой из молекул растворителя. Если растворитель — вода, то оболочка называется гидратной, а процесс — гидратацией. Для данного механизма определяющим фактором является прочность связи между сольватной оболочкой и поверх­ностью дисперсной фазы. До тех пор, пока эта связь настолько прочна, что с увеличением скорости деформации удерживает оболочку на поверхности частицы, вязкость не уменьша­ется. Однако с увеличением градиента скорости больше определенной величины происходит постепенный отрыв сначала верхних, а затем и более глубоких слоев сольватных оболочек. Частицы дисперсной фазы при этом как бы «освобождаются».

Если учесть, что кажущаяся вязкость псевдопластической среды является функцией объема структуры, то становится понятным, почему описанное явление сопровождается уве­личением текучести — наступает уменьшение фактической объемной концентрации дис­персной фазы. Процесс снижения вязкости продолжается до тех пор, пока все сольватные оболочки не разрушатся. Согласно данным Б.М. Смольского и соавт. (1970), обязательное превышение кажущейся вязкости при относительно низких скоростях деформации над вяз­костью при достаточно высоких градиентах скорости объясняется тем, что, во-первых, при малых скоростях деформации прохождение дисперсной среды через сольватированные час-

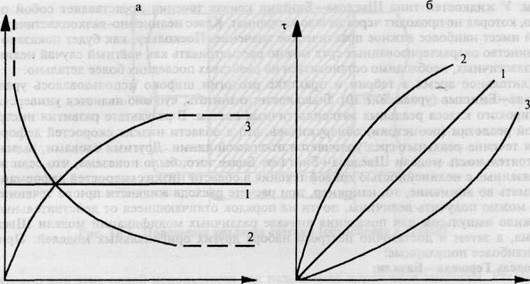
Рис. 10.5. Кривые вязкости (а) и течения (б) ньютоновской (1), псевдопластичной (2) и дилансной

жидкостей (3).

тицы «затруднено» более, чем в случае больших скоростей сдвига, и, во-вторых, взаимодей­ствие между частицами более выражено ввиду их больших относительных размеров при низ­ких скоростях деформации. По-видимому, имеют место оба механизма возникновения псев­допластичности.

Реже, чем псевдопластичные, встречаются дилансные среды. Индекс течения п у них больше единицы. Это означает, что вязкость у таких материалов увеличивается с ростом ско­рости деформации. Кривые течения и вязкости такой среды представлены на рис. 10.5, а, график 3. Явление дилансии впервые обнаружено О. Рейнольдсом. Необходимо различать реологическую и объемную дилансию. Явление реологической дилансии состоит в увеличе­нии вязкости с ростом скорости деформации вследствие увеличения объема дисперсной фазы системы при деформирующем воздействии. Как более общий случай реологической дилансии можно выделить объемную дилансию, при которой увеличение объема дисперсной фазы не сопровождается изменением кажущейся вязкости среды. Общепринятое толкование дилансии заключается в том, что при сдвиге как бы изменяется «упаковка» частиц твердой дисперсной фазы, она становится более «свободной». Это в свою очередь приводит к увели­чению относительного объема дисперсной фазы. Возникновение такой своеобразной «по­ристой» структуры, в которой жидкие элементы дисперсионной среды сочетаются со своего рода элементами «пустоты», и приводит к феномену дилансии.

До сих пор речь шла о текучих средах с так называемой стационарной реологией. К жидкостям с нестационарной реологией относятся такие, которые обладают свойствами тиксотропии и реопексии. Сущность тиксотропии заключается в том, что при течении с по­стоянной скоростью деформации неньютоновская жидкость со временем становится нью­тоновской (подчеркнем, что псевдопластичные и дилансные среды также ведут себя как ньютоновские, но лишь в определенных пределах скоростей деформации). В отличие от псевдопластичных сред, структура которых начинает меняться с ростом скорости деформа­ции постепенно, у тиксотропных сред для этого требуется время.

Явлением, противоположным тиксотропии, является реопексия, или антитиксотропия. Среды, обладающие свойством реопексии, характеризуются тем, что их вязкость увеличива­ется в результате возникновения течения. В отличие от дилансных сред для изменения структуры реопектической жидкости необходимо, чтобы прошло определенное время после начала воздействия деформаций.

Таким образом, нами кратко рассмотрены все типы неньютоновских жидкостей в соот­ветствии с приведенной выше классификацией, за исключением нелинейно-вязкопластичных жидкостей. Само название этого типа жидкостей говорит о том, что их главной особенностью является сочетание пластичности и вязкости с уклонением кривых течения от линейной

формы. У жидкостей типа Шведова—Бингама кривая течения представляет собой прямую линию, которая не проходит через начало координат. Класс нелинейно-вязкопластичных жид­костей имеет наиболее важное практическое значение. Поскольку, как будет показано ниже, большинство охарактеризованных сред можно рассматривать как частный случай нелинейно-вязкопластичных, необходимо остановиться на свойствах последних более детально.

Длительное время в теории и практике реологии широко использовалось уравнение Шведова—Бингама (уравнение 10). Было принято считать, что оно является универсальным для широкого класса реальных вязкопластичных систем. В результате развития инструмен­тальной реологии (реометрии) обнаружилось, что в области низких скоростей деформации кривая течения реальных сред уклоняется от прямой линии. Другими словами, выяснилась несостоятельность модели Шведова—Бингама. Более того, было показано, что если эффек­ты, связанные с нелинейностью кривой течения в области низких скоростей деформации, не принимать во внимание, то, например, при расчете расхода жидкости при ее течении через трубы можно получить величины, почти на порядок отличающиеся от действительных. Это послужило импульсом для появления вначале различных модификаций модели Шведова— Бингама, а затем и достаточно пестрого набора других оригинальных моделей. Приведем лишь наиболее популярные:

модель Гершеля—Балкли:

т = т₀ + к ■ у'

(15)

(модель получена путем добавления к пределу текучести степенного закона, описывающего поведение псевдопластических и дилансных жидкостей); модель Кессона:

(16)

= Vt₀ + у1ц ■ у ;

модель Шульмана:

(17)

Между тем, несмотря на обилие моделей, ни одна из них не является универсальной для всего спектра скоростей деформации. Наибольшего интереса заслуживает модель Шульмана, которая характерна тем, что из нее выводится ряд других реологических законов. Например, при п = 1 она превращается в модель Шведова, а при п = 2 — в модель Кессона. Однако и модель Шульмана, по мнению самого же автора, не всегда позволяет использовать ее для аппроксимации всей кривой течения реальной жидкости.

Позднее З.П. Шульманом (1976) предложена более обобщенная реологическая модель:

_т1/п ₌

Vl/in

(18)

где п, m — индексы течения.

Эта модель предполагает нелинейность пластичности и вязкости. Она в сущности вклю­чает в себя большинство имеющихся реологических уравнений.

Подводя итог, можно сказать, что, во-первых, существует целый класс сред или реоло­гических систем, которые могут быть охарактеризованы как неньютоновские текучие систе­мы (неньютоновские жидкости). Их отличительной чертой является наличие переменной вязкости. Во-вторых, переменная вязкость (в смысле ц/у) может быть обусловлена либо не­линейной зависимостью между текучестью и градиентом скорости (т₀ = 0), либо, наоборот, наличием предела текучести (т₀ # 0), либо тем и другим вместе. В-третьих, для описания та­кого рода текучих систем существует несколько реологических уравнений. Наиболее обоб­щающим из них является уравнение Шульмана (18).

Очевидно, что в зависимости от особенностей конкретной нелинейно-вязкопластичной среды индексы пит должны подбираться индивидуально — применительно к каждому ма­териалу. Чем более строго они будут определены, тем точнее можно будет отразить реологи­ческие особенности той или иной жидкости.

Реологические свойства различных текучих систем важны, безусловно, не сами по себе, а главным образом в связи с тем, что они нередко определяют резкие отличия в параметрах течения этих сред. Рассмотрим, как сказываются реологические особенности неньютонов­ских жидкостей на характеристике расхода потока и профилях скоростей при течении в ци­линдрической трубке.

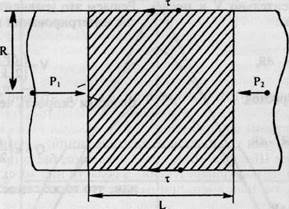Рис. 10.6. Поршневая аналогия течения (объяснение в тексте).

Обычно для этих целей используется так называемая поршневая аналогия. Рассмотрим отрезок трубки радиусом г и длиной 1. Представим внутри ее цилиндрический элемент жид­кости («поршень») радиусом R и длиной L (рис. 10.6). На этот элемент с торцов действуют давления Р, и Р₂, разница между которыми ЛР приводит его в равномерное движение (при

Р. * Р₂)-

Силы давления F, и F₂, действующие на торцы, будут соответственно равны:

F, - nR² P,

P2

F₂ =

Кроме того, на этот элемент действуют силы сопротивления, обусловленные наличием касательных напряжений, действующих по его периметру. Они равны 27iR.Lt. Силы давления и силы сопротивления противоположны по направлению и при равномерном движении равны, т. е. 2tiRLt = 71R² • АР:

х =

2L

дР R • ДР

2tiRL

Таким образом, мы получили функциональную зависимость, связывающую напряжения с геометрией (размерами) трубки. Из полученного уравнения следует, что напряжение, воз­никающее по периметру цилиндрического элемента, при прочих равных условиях всегда пропорционально перепаду давления в системе.

Проанализируем, какие отличия возникают при таком течении между ньютоновской и неньютоновской жидкостями. В качестве неньютоновской рассмотрим псевдопластичную жидкость, подчиняющуюся степенному закону. В левом столбце будем рассчитывать показа­тели течения ньютоновской, а в правом — неньютоновской жидкости.

Ньютоновская жидкость